决策论——贝叶斯后验概率R和Python实现(一)
贝叶斯理论是决策领域的一个重要分支，属于风险型决策的范畴。风险型决策的基本方法是将状态变量看成随机变量，用先验分布表示状态变量的概率分布，用期望值准则计算方案的满意程度。但是在日常生活中，先验分布往往存在误差，为了提高决策质量，需要通过市场调查来收集补充信息，对先验分布进行修正，然后用后验分布来决策，这就是贝叶斯决策。
一、贝叶斯应用示例
先验概率: 一所学校里面有 60% 的男生，40% 的女生。男生总是穿长裤，女生则一半穿长裤一半穿裙子。有了这些信息之后我们可以容易地计算“随机选取一个学生，他（她）穿长裤的概率和穿裙子的概率是多大”，这个就是前面说的“先验概率”的计算。
后验概率: 假设你走在校园中，迎面走来一个穿长裤的学生（很不幸的是你高度近似，你只看得见他（她）穿的是否长裤，而无法确定他（她）的性别）,你能够推断出他（她）是女生的概率是多大吗？这就是所谓的“后验概率”。
将上例转化为分类问题，则类别\(c\)={男,女}，学生个体为样本\(x\)，其中\(x\in X\)，其中随机变量\(X\)是一维向量，只有唯一的属性：\(性别\)∈{长裤,裙子}
先验概率的计算：
表示随机选取一个学生，他（她）穿长裤的概率的概率。
后验概率的计算：
表示一个穿长裤的学生是女生的概率。
在求解后验概率的公式中，我们用到了以下两个公式：
上面就是常用的贝叶斯公式，它提供了一种从\(P(c),P(x)\)和\(P(x|c)\)计算后验概率的方法，如下图所示。
| 公式 | 含义 |
|---|---|
| \(x\) | 属性 |
| \(c\) | 类别 |
| \(P(c|x)\) | 后验概率（给定预测变量的类的后验概率） |
| \(P(x|c)\) | 似然概率（预测器给定类的概率的可能性） |
| \(P( c )\) | 先验概率（类的先验概率） |
| \(P( x )\) | 边际似然概率（预测器的先验概率） |
二、贝叶斯公式
让我们从一个摸球的例子来理解条件概率。我们有两个桶：灰色桶和绿色桶，一共有7个小球，4个蓝色3个紫色，分布如下图：
从这7个球中，随机选择1个球是紫色的概率\(p\)是多少？
选择过程如下：先选择桶,再从选择的桶中选择一个球。
上述我们选择小球的过程就是信息不断明确的过程，条件概率形成的过程，在选择桶的颜色的情况下是紫色的概率，另一种计算条件概率的方法是贝叶斯准则。
贝叶斯公式是英国数学家贝叶斯提出的一个数据公式:
\(p(A,B)\)：表示事件A和事件B同时发生的概率。
\(p(B)\)：表示事件B发生的概率，叫做先验概率；p(A)：表示事件A发生的概率。
\(p(A|B)\)：表示当事件B发生的条件下，事件A发生的概率叫做后验概率。
\(p(B|A)\)：表示当事件A发生的条件下，事件B发生的概率。
偷窃与狗吠:住在一座别墅里的一家人，在过去的 1 年中，发生了 2 次盗窃，这家人养了一只狗，这只狗平均每周晚上叫 3 次，而且，当发生盗窃时，这只狗会叫的概率是 0.9，那么在这只狗叫的情况下，发生盗窃的概率是多少？
我们假设 A 事件是狗晚上叫，则 P(A) = 3/7 ，假设 B 事件是发生盗窃，则P(B) = 2/365 。我们还知道，当 B 事件发生的条件下，A 事件发生的概率 P(A|B) = 0.9 。因此，根据贝叶斯公式，我们推断得到，狗叫时，发生盗窃的概率，即：\[p(B|A)=\frac{p(A,B)}{p(A)}=\frac{p(A|B) p(B)}{p(A)}（结果略） \]
我们用一句话理解贝叶斯：世间很多事都存在某种联系，假设事件A和事件B。人们常常使用已经发生的某个事件去推断我们想要知道的之间的概率。例如，医生在确诊的时候，会根据病人的舌苔、心跳等来判断病人得了什么病。对病人来说，只会关注得了什么病，医生会通道已经发生的事件来确诊具体的情况。这里就用到了贝叶斯思想，A是已经发生的病人症状，在A发生的条件下是B发生的概率。
三、后验概率的手工计算
例1：假设有三种类型的硬币，分别是硬币ABC。 硬币ABC投出正面的概率分别为 0.5,0.6 和0.9。 我们有个抽屉，里面放了5枚硬币，其中A类2枚，B类2枚，C类1枚。 小明从5个硬币中随机拿一枚，投一次，发现这次投出了正面。 请问这枚硬币最有可能是ABC类的哪一种？
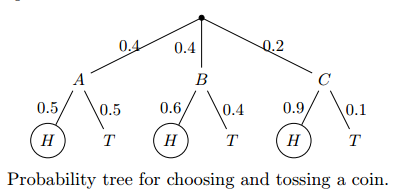
【解析】小明先随机拿骰子，概率分别为0.4,0.4,0.2， 然后这三个骰子掷出正面的概率分别为0.5,0.6,0.9， 已知结果为下图画圈的H，设为事件D，那么小明拿到硬币A、B或C的概率就是求后验概率。
先验概率为：
\(P(A)= 0.4 \quad P(B) = 0.4 \quad P(C) = 0.2\)
在ABC 三个筛子下 投出正面的概率为：
\(P(D|A)= 0.5\quad P(D|B) = 0.6 \quad P(D|C) = 0.9\)
我们要求的是已知D为正面的情况下，这枚硬币是A、B或C的概率是多少？ 也就是说要比较以下三个数字的大小：
\(P(A|D)\quad P(B|D)\quad P(C|D)\)
利用贝叶斯公式， 我们还有一个概率\(P(D)\)并不知道，但我们可以算，因为“D = 正面”发生的概率是所有条件下发生“D=正面”概率的和。用公式表示就是这样：
好了，我们没有未知的了,代入就能比较大小。
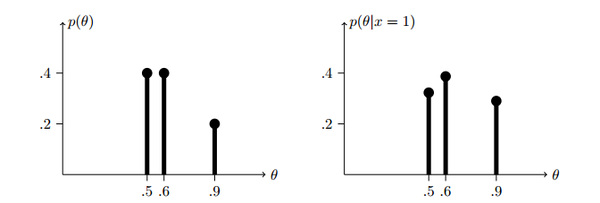
从上图我们可以看到，已知第一次掷骰子的结果为正面，那么小明最有可能拿到的是B类骰子。这样我们就完成了一次贝叶斯更新。
如果小明再用这个骰子掷一次硬币，这次的结果也是正面，那么小明手里的硬币为ABC的概率分别是多少？ 我们可以把第一次的后验概率\(P(A|D)\) 作为这次的先验概率，然后再进行一次贝叶斯更新，计算出后检验概率，代入贝叶斯公式。
同理可计算出\(P(B|D_1=1,D_2=1)\)和\(P(C|D_1=1,D_2=1)\)的概率，代入数字可以得到：
有的人已经发现了。倒数第二步的分母是常数，这个常数只是为了保证所有的后验概率的和为1, 那么其实我们根本就不需要计算\(P(D)\)， 只需计算分子，在扩大或缩小几倍，让他们的和为1 就行了。这两个贝叶斯更新可以用下图表示出来
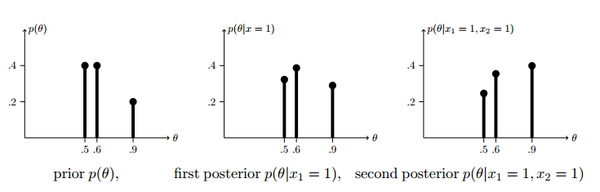
以上就是先验概率为离散数据时更新后验概率的方法。
四、后验概率的软件计算
例2：这里使用西瓜数据集3.0部分数据如下：
| 色泽 | 青绿 | 乌黑 | 乌黑 | 青绿 | 浅白 | 青绿 |
|---|---|---|---|---|---|---|
| 好瓜 | 是 | 是 | 是 | 是 | 是 | 否 |
| 色泽 | 青绿 | 乌黑 | 乌黑 | 乌黑 | 青绿 | 乌黑 |
| 好瓜 | 是 | 是 | 是 | 否 | 否 | 否 |
| 色泽 | 浅白 | 浅白 | 青绿 | 浅白 | 乌黑 | 浅白 |
| 好瓜 | 否 | 否 | 否 | 否 | 否 | 否 |
收集的样本容量为18。这里色泽\(x\)是西瓜的特征变量，其可取值（青绿,乌黑,浅白）；好瓜\(y\)可取值(是，否)两个分类，当然可转化为分类值（-1,1）来表示。目前有一个新瓜，其色泽为“乌黑”，试用贝叶斯公式确定y的取值，即求后验概率。
4.1 分步计算
【解析】
先验概率\(P(y)\)为:
options(digits=4)
library(openxlsx)
data=read.xlsx("melon5.xlsx")
#先验概率
prior.yes = sum(data[,2] == "是") / length(data[,2])
prior.no = sum(data[,2] == "否") / length(data[,2])
似然概率（条件概率）\(P(x|y)\)为:
#似然概率
likeli=table(data[,2],data[,1]) #注意变量先后
likeli[1,]=likeli[1,]/sum(data[,2] == "否")
likeli[2,]=likeli[2,]/sum(data[,2] == "是")
likeli
浅白 青绿 乌黑
否 0.400 0.300 0.300
是 0.125 0.375 0.500
后验概率\(P(y|x)\)为：
posti=likeli
prior=cbind(prior.no,prior.yes)
xpr=prior %*% likeli
for (i in 1:(dim(likeli)[2])) {
posti[1,i]=likeli[1,i]* prior[1] /xpr[i]
posti[2,i]=likeli[2,i] * prior[2] /xpr[i]
}
#后验概率
posti #第三列就是上面示例的后验概率
浅白 青绿 乌黑
否 0.8000 0.5000 0.4286
是 0.2000 0.5000 0.5714
4.2 完整的R程序
# ============================================================
# 贝叶斯分类计算示例：西瓜数据集3.0（色泽-好瓜关系）
# ============================================================
# 构造数据框 -------------------------------------------------
color <- c("青绿","乌黑","乌黑","青绿","浅白","青绿",
"青绿","乌黑","乌黑","乌黑","青绿","乌黑",
"浅白","浅白","青绿","浅白","乌黑","浅白")
label <- c("是","是","是","是","是","否",
"是","是","是","否","否","否",
"否","否","否","否","否","否")
data <- data.frame(color, label)
n <- nrow(data)
cat("样本总数 n =", n, "\n\n")
# ------------------------------------------------------------
# 1. 计算先验概率 P(y)
# ------------------------------------------------------------
prior_table <- prop.table(table(data$label))
prior_table
cat("\n先验概率 P(y):\n")
print(round(prior_table, 4))
# ------------------------------------------------------------
# 2. 计算似然概率 P(x|y)
# ------------------------------------------------------------
likeli_table <- table(data$label, data$color)
likeli_prob <- prop.table(likeli_table, margin = 1) # 按行归一化
cat("\n似然概率 P(color | label):\n")
print(round(likeli_prob, 4))
# ------------------------------------------------------------
# 3. 计算证据概率 P(x)
# ------------------------------------------------------------
evidence <- prop.table(table(data$color))
cat("\n证据概率 P(color):\n")
print(round(evidence, 4))
# ------------------------------------------------------------
# 4. 计算后验概率 P(y|x) = [P(x|y)*P(y)] / P(x)
# ------------------------------------------------------------
posterior <- matrix(0,
nrow = length(evidence),
ncol = length(prior_table),
dimnames = list(names(evidence), names(prior_table)))
for (c in names(evidence)) {
for (y in names(prior_table)) {
posterior[c, y] <- (likeli_prob[y, c] * prior_table[y]) / evidence[c]
}
}
cat("\n后验概率 P(label | color):\n")
print(round(posterior, 4))
# ------------------------------------------------------------
# 5. 针对色泽 = “乌黑” 的后验概率
# ------------------------------------------------------------
color_interest <- "乌黑"
p_yes_given_black <- posterior[color_interest, "是"]
p_no_given_black <- posterior[color_interest, "否"]
cat("\n针对色泽 = '乌黑'：\n")
cat(sprintf("P(好瓜 = 是 | 色泽 = 乌黑) = %.4f\n", p_yes_given_black))
cat(sprintf("P(好瓜 = 否 | 色泽 = 乌黑) = %.4f\n", p_no_given_black))
4.3 完整的Python程序
import pandas as pd
# 构造数据（18 条）
colors = [
"青绿","乌黑","乌黑","青绿","浅白","青绿",
"青绿","乌黑","乌黑","乌黑","青绿","乌黑",
"浅白","浅白","青绿","浅白","乌黑","浅白"
]
labels = [
"是","是","是","是","是","否",
"是","是","是","否","否","否",
"否","否","否","否","否","否"
]
df = pd.DataFrame({"color": colors, "label": labels})
n = len(df)
# 先验 P(y)
priors = df['label'].value_counts().sort_index() # counts
priors_prop = df['label'].value_counts(normalize=True).sort_index()
# 似然 P(x|y)
likelihood_counts = df.groupby('label')['color'].value_counts().unstack(fill_value=0).sort_index(axis=1)
likelihood_prob = likelihood_counts.div(likelihood_counts.sum(axis=1), axis=0)
# 证据 P(x)
evidence = df['color'].value_counts().sort_index() / n
# 后验 P(y|x) 对每个色泽计算
posterior = pd.DataFrame(index=evidence.index, columns=priors_prop.index, dtype=float)
for color in evidence.index:
for lab in priors_prop.index:
p_x_given_y = likelihood_prob.loc[lab, color]
p_y = priors_prop[lab]
p_x = evidence[color]
posterior.loc[color, lab] = (p_x_given_y * p_y) / p_x
# 输出（四位小数）
print("样本总数 n =", n)
print("\n先验（概率）:\n", priors_prop.to_string(float_format=lambda x: f"{x:.4f}"))
print("\n似然 P(color | label)（概率）:\n", likelihood_prob.round(4))
print("\n证据 P(color):\n", evidence.round(4).to_string())
print("\n后验 P(label | color):\n", posterior.round(4))
# 针对色泽 = "乌黑" 的后验概率
color_of_interest = "乌黑"
post_yes_given_wuhei = posterior.loc[color_of_interest, "是"]
post_no_given_wuhei = posterior.loc[color_of_interest, "否"]
print(f"\n针对色泽 = '{color_of_interest}'：")
print(f"P(好瓜 = 是 | 色泽 = {color_of_interest}) = {post_yes_given_wuhei:.4f}")
print(f"P(好瓜 = 否 | 色泽 = {color_of_interest}) = {post_no_given_wuhei:.4f}")
总结
贝叶斯后验概率是一种学习机制。先验概率不是根据有关自然状态的全部资料测定的，而只是利用现有的材料(主要是历史资料)计算的；后验概率是指在得到“结果”的信息后重新修正的概率，是“执果寻因”问题中的"果"。后验概率使用了有关自然状态更加全面的资料，既有先验概率资料，也有补充资料；先验概率的计算比较简单，没有使用贝叶斯公式；而后验概率的计算，要使用贝叶斯公式，而且在利用样本资料计算逻辑概率时，还要使用理论概率分布，需要更多的数理统计知识。
浙公网安备 33010602011771号