矩阵可以被看成一个表格,每个格里面只能放数字的表格。“矩”的意思是矩形,由数字组成的矩形;“阵”的意思是整齐,这些数字排列起来是非常整齐的,并不会歪歪扭扭;矩阵中,横向的数字是行,竖向的数字是列,行和列都是整数,可以是1或者是\(n\)(\(n\)是整数);矩阵中,通过“第几行、第几列”这种简便的方式来确定某个数字的具体位置。矩阵是一个数据集成的符号,我们可把矩阵\(A\)看成是由若干个行向量组成的,批处理是矩阵运算中很重要的一个观点。
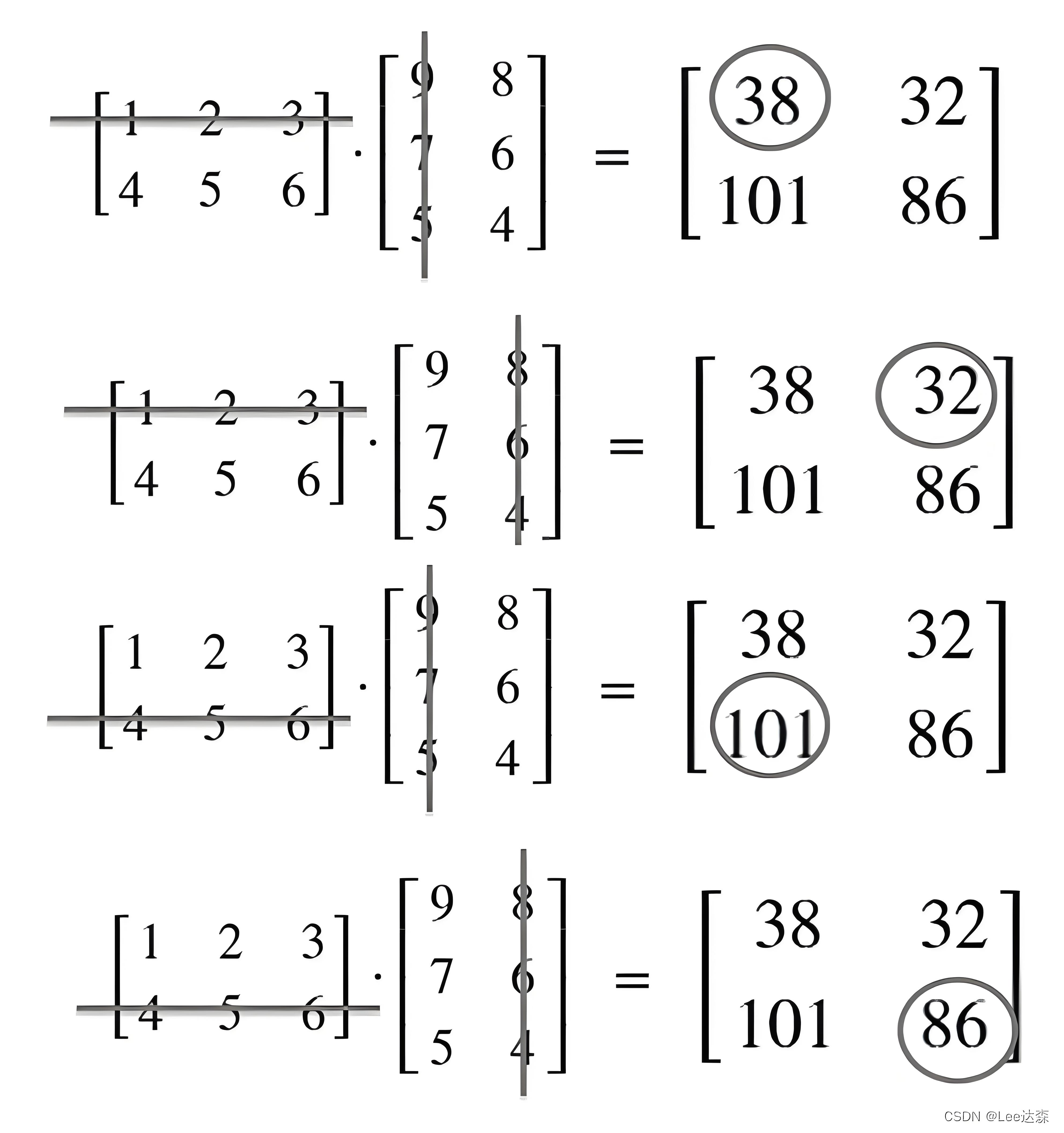
一 矩阵乘法的规则
矩阵乘法(英文:matrix multiplication)是一种根据两个矩阵得到第三个矩阵的二元运算,第三个矩阵即前两者的乘积,称为矩阵积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义。即:
| 矩阵乘法示意1 |
矩阵乘法示意2 |
 |
 |
二 消元法的矩阵实现
消元法(elimination)是求解线性方程组的根本方法。消元法如果奏效了,方程就解出来了。消元法通过对线性方程组施行三种初等变换:
互换两个方程的位置;
把一个方程的倍数加到另一个方程;
用一非零的数乘某一方程。
将原方程组中某方程的某个未知量的系数为零——消去这个元;反复这样做,得到一个化简的线性方程组,这个是阶梯型方程组(系数及常数项均变为0的方程可去掉,因而方程个数未必与原方程个数相等),这样的阶梯型线性方程组容易判断是不是有解;有解时,容易得到所有的解,这就是用消元法求解的过程。
2.1 消元法示例
\[\begin{cases}
2x+4y-2z=2&(1)\\4x+9y-3z=8&(2)\\-2x-3y+7z=10&(3)
\end{cases}
\]
第一步,方程 (2) 减去 2 倍的方程(1),得到$ y+z=4$;
第二步,方程(3) 加上 1 倍的方程 (1),得到 \(y+5z=12\);
第三步,上面得到的两个方程相减,得到 \(4z=8\)。
\begin{alignedat}{2} \boldsymbol 2&x \space+\space&4&y \space-\space&2&z=\space 2 \\ & \space\space&\boldsymbol 1&y \space+\space&1&z=\space 4\\ & \space\space&& \space\space&\boldsymbol 4&z=\space 8 \end{alignedat}
三个主元分别为 2, 1, 4,然后我们就可以用回带法求出方程组的解。
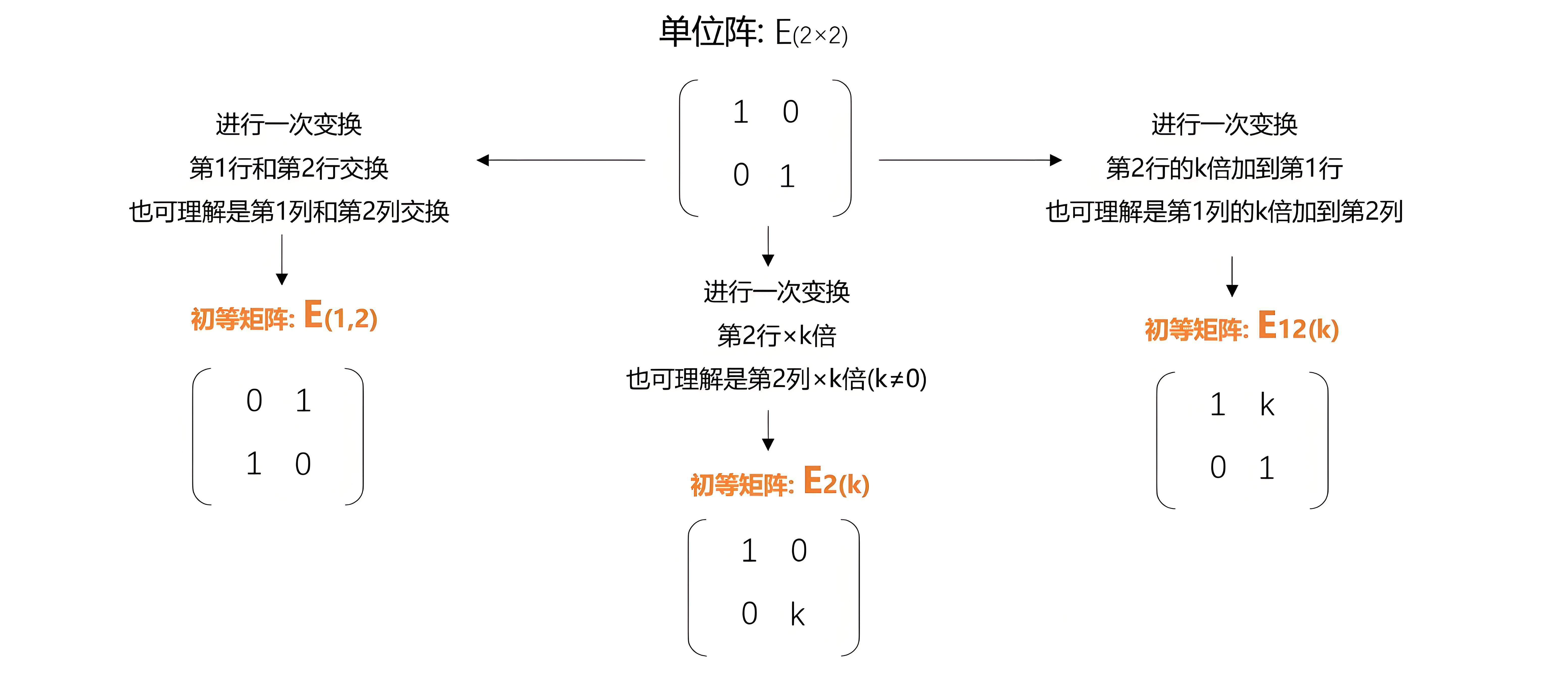
2.2 初等矩阵
初等矩阵(elementary matrix):初等矩阵是指由单位矩阵经过一次初等变换(single elementary row operation)得到的矩阵,共有三种形式:

前面提到每经过一次初等行变换,都是对原矩阵左乘一个初等矩阵。所以我们很容易通过左乘多个初等矩阵来表示一个矩阵通过一些初等行变换后变为另一个矩阵的过程,参看下例:
\[A=\begin{bmatrix} 1 & 0 & 2 \\ 2 & -1 & 3 \\ 1 & 4 & 4\end{bmatrix}B=\begin{bmatrix} 1 & 0 & 2 \\ 0 & -1 & -1 \\ 0 & 0 & -2\end{bmatrix}
\]
我们想将 $\boldsymbol{A} $变换到 $\boldsymbol{B} $的过程写成 $$\boldsymbol{B}=\boldsymbol{E}_{k} \boldsymbol{E}_{k-1} \cdots \boldsymbol{E}_{1} \boldsymbol{A}$$ 形式,进行行变换
\[\boldsymbol{A} = \left(\begin{array}{ccc}
1 & 0 & 2 \\
2 & -1 & 3 \\
1 & 4 & 4
\end{array}\right)\xrightarrow[\boldsymbol{E}_1]{R_2-2 R_1}\left(\begin{array}{ccc}
1 & 0 & 2 \\
0 & -1 & -1 \\
0 & 4 & 2
\end{array}\right) \xrightarrow[\boldsymbol{E}_2]{R_3- R_1}\left(\begin{array}{ccc}
1 & 0 & 2 \\
0 & -1 & -1 \\
0 & 0 & -2
\end{array}\right) \xrightarrow[\boldsymbol{E}_3]{R_3+4 R_2}\left(\begin{array}{ccc}
1 & 0 & 2 \\
0 & -1 & -1 \\
0 & 0 & -2
\end{array}\right) =\boldsymbol{B}
\]
\[\boldsymbol{E}_{\mathbf{1}}=\left(\begin{array}{ccc}
1 & 0 & 0 \\
-2 & 1 & 0 \\
0 & 0 & 1
\end{array}\right) \boldsymbol{E}_2=\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
-1 & 0 & 1
\end{array}\right) \quad E_3=\left(\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 4 & 1
\end{array}\right)
\]
所以 $$E_3E_2E_1A=B$$
我们也可以推出
\[A=E_1^{-1}E_2^{-1}E_3^{-1}B
\]
其中
\[E_1^{-1}=\begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}E_2^{-1}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}E_3^{-1}\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -4 & 1 \end{bmatrix}
\]
2.3 消元法的矩阵表示
\[\begin{cases}
2x_1+4x_2-2x_3=2\\4x_1+9x_2-3x_3=8\\-2x_1-3x_2+7x_3=10
\end{cases}
\leftrightarrow
\begin{bmatrix} 2&4&-2 \\ 4&9&-3\\-2&-3&7\end{bmatrix} \begin{bmatrix} x_1 \\ x_2\\x_3 \end{bmatrix} = \begin{bmatrix} 2 \\ 8\\10 \end{bmatrix}
\]
互换两个方程的位置
比如交换一个方程和第二个方程,考虑方程的增广矩阵,引入相应的初等矩阵左乘,即
\[\begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0\end{bmatrix}\begin{bmatrix}2&4&-2&2 \\ 4&9&-3&8\\-2&-3&7& 10\end{bmatrix}=\begin{bmatrix} 4&9&-3&8\\2&4&-2&2 \\-2&-3&7& 10\end{bmatrix}
\]
把一个方程的倍数加到另一个方程
第 (2) 个方程减去第(1)个方程的 2 倍,可以得到:
\[\begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 1 & 0 & 0\end{bmatrix}\begin{bmatrix}2&4&-2&2 \\ 4&9&-3&8\\-2&-3&7& 10\end{bmatrix}=\begin{bmatrix} 2&4&-2&2 \\0&1&1&4 \\-2&-3&7& 10\end{bmatrix}
\]
用一非零的数乘某一方程
将第 (1)个方程乘以\(1/2\) ,可以得到:
\[\begin{bmatrix} 1/2 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0\end{bmatrix}\begin{bmatrix}2&4&-2&2 \\ 4&9&-3&8\\-2&-3&7& 10\end{bmatrix}=\begin{bmatrix} 1&2&-1&1 \\0&1&1&4 \\-2&-3&7& 10\end{bmatrix}
\]
从上面过程可知,你想如何消元就可以用同样的初等矩阵左乘线性方程组的增广矩阵,这样初等矩阵可以实现消元法的各个步骤,从而矩阵可以用来求解线性方程组,得到线性方程组的基础解系。因此我们可以用结构化的程序算法,实现计算机迭代求解线性方程组,这是线性方程组求解的时代要求与发展,给矩阵在各个领域的应用打开了窗口。
三 矩阵乘法在管理中的实践
3.1 农场产量汇总
假设有这样一个问题。东郊农场、西郊农场和北郊农场都种植土豆、萝卜、红薯和花生。你在了解了今年这3个农场所有作物的产量(吨)后,想将产量情况汇报给你的上级。你会怎么做呢?你很可能会想到用一个表格来直观地表示:
|
土豆 |
萝卜 |
红薯 |
花生 |
| 东郊 |
45 |
37 |
29 |
18 |
| 西郊 |
22 |
26 |
37 |
15 |
| 北郊 |
34 |
27 |
21 |
41 |
如果只看数字部分的话,我们刚刚做出的表格就可以看作是一个矩阵。而当你从市场上得知了今年这四种作物的价格(万元/吨)后,土豆 3、萝卜 4、红薯 2、花生 5,你估算出了这几个农场今年的收益(万元)。从这几个农场每种产品的产量和单价到各个农场的总收入,这中间是怎么计算的呢?只需把每个农场每种作物的产量分别乘以单价,再求和即可。这个过程就是矩阵乘法的应用,写成矩阵的形式就是:
\[\begin{bmatrix} 45 & 37 & 29&18\\ 22 & 26 & 37&15\\ 34&27&21&41 \end{bmatrix} \times
\begin{bmatrix} 3\\ 4\\ 2\\ 5 \end{bmatrix} = \begin{bmatrix} 431\\ 319\\457 \end{bmatrix}
\]
矩阵的乘法中需要注意的是,由于是表格相乘,所以并不满足乘法交换律。且第一个表格的列数要等于第二个表格的行数才行,因为结果表格中第\(m\)行\(n\)列的元素是由第一个表格中的\(m\)行和第二个表格中\(n\)列中的元素对应相乘并求和得到的。如上例中的3行4列矩阵×4行1列矩阵=3行1列矩阵。同时可以发现所得的矩阵的行列数等于第一个矩阵的行数和第二个矩阵的列数。
有了矩阵的乘法的计算方式之后,一些复杂繁琐的线性关系就可以方便地用矩阵来表示了。如:
\[y_1=a_{11}x_1+a_{12}x_2+a_{13}x_3\\
y_2=a_{21}x_1+a_{22}x_2+a_{23}x_3\\
y_3=a_{31}x_1+a_{32}x_2+a_{33}x_3
\]
就可以表示为 $Y=AX $,其中
\[Y= \begin{bmatrix} y_1\\ y_2\\ y_3 \end{bmatrix}
X=\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}
\]
\[A= \begin{bmatrix} a_{11}& a_{12} & a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{bmatrix}
\]
再如
\[y_1=b_{11} x_1+b_{12} x_2+b_{13} x_3+b_{14} x_4\\
y_2=b_{21} x_1+b_{22} x_2+b_{23} x_3+b_{24} x_4\\
y_3=b_{31} x_1+b_{32} x_2+b_{33} x_3+b_{34} x_4\\
y_4=b_{41} x_1+b_{42} x_2+b_{43} x_3+b_{44} x_4
\]
可以表示为 $ Y=BX $,其中
\[Y= \begin{bmatrix} y_1\\ y_2\\ y_3 \end{bmatrix}; X= \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix}
\]
\[B= \begin{bmatrix} b_{11}&b_{12}&b_{13}&b_{14}\\ b_{21}&b_{22}&b_{23}&b_{24}\\ b_{31}&b_{32}&b_{33}&b_{34}\end{bmatrix}
\]
反过来讲,矩阵\(A\)和\(B\)都可以写成\(y\)和\(x\)组成的方程组的形式,而方程组代表着从\((x_1,x_2,x_3)\)或\((x_1,x_2,x_3,x_4)\)到\((y_1,y_2,y_3)\) 的线性变换。也就是说,矩阵和线性变换存在着一一对应的关系,那么矩阵就可以作为一种研究线性变换的工具使用了。
3.2 生产计划与资源分配
在制造企业中,常常面临这样的问题:如何合理安排多种产品的生产计划,才能最大化利用资源? 这正是线性代数和矩阵乘法能发挥作用的地方。设某公司生产三种产品:A、B 和 C。它们分别需要三种资源:原料、水、电。每种产品的单位产出所需资源如下(单位:单位资源/件):
|
原料 |
水 |
电 |
| 产品A |
2 |
1 |
3 |
| 产品B |
1 |
2 |
2 |
| 产品C |
4 |
1 |
1 |
如果本月计划生产产品A 100 件、B 150 件、C 200 件,问应准备多少资源?
我们可以将资源消耗矩阵表示为:
\[M = \begin{bmatrix} 2 & 1 & 3 \\ 1 & 2 & 2 \\ 4 & 1 & 1 \end{bmatrix}
\]
生产计划表示为列向量:
\[P = \begin{bmatrix} 100 \\ 150 \\ 200 \end{bmatrix}
\]
则资源总需求为:
\[R = M^T \cdot P = \begin{bmatrix} 2 & 1 & 4 \\ 1 & 2 & 1 \\ 3 & 2 & 1 \end{bmatrix} \cdot \begin{bmatrix} 100 \\ 150 \\ 200 \end{bmatrix} = \begin{bmatrix} 2 \times 100 + 1 \times 150 + 4 \times 200 \\ 1 \times 100 + 2 \times 150 + 1 \times 200 \\ 3 \times 100 + 2 \times 150 + 1 \times 200 \end{bmatrix} = \begin{bmatrix} 1050 \\ 600 \\ 850 \end{bmatrix}
\]
也就是说,本月需准备原料 1050 单位、水 600 单位、电 850 单位。
✅ 管理意义:通过矩阵乘法,不仅可快速计算资源总需求,还能在资源受限时进行反向推算(即给定资源总量,反推可生产数量),提高计划的科学性和透明度。
3.3 投资组合收益预测
在金融管理中,矩阵乘法也有广泛的应用,特别是在投资组合分析与收益预测中。一位投资经理配置了四种金融资产:股票、债券、货币基金和房地产基金。在未来一个季度内,这些资产的预期收益率为:
- 股票:8%
- 债券:5%
- 货币基金:3%
- 房地产基金:6%
现有三位客户分别选择了不同的投资组合方案(单位:万元):
|
股票 |
债券 |
货币基金 |
房地产基金 |
| 客户A |
20 |
30 |
10 |
40 |
| 客户B |
50 |
10 |
20 |
20 |
| 客户C |
10 |
20 |
50 |
20 |
我们用一个 \(3 \times 4\) 的投资矩阵表示:
\[I = \begin{bmatrix} 20 & 30 & 10 & 40 \\ 50 & 10 & 20 & 20 \\ 10 & 20 & 50 & 20 \end{bmatrix}
\]
收益率列向量:
\[r = \begin{bmatrix} 0.08 \\ 0.05 \\ 0.03 \\ 0.06 \end{bmatrix}
\]
则三位客户的预期收益(万元)为:
\[E = I \cdot r = \begin{bmatrix} 20 \times 0.08 + 30 \times 0.05 + 10 \times 0.03 + 40 \times 0.06 \\ 50 \times 0.08 + 10 \times 0.05 + 20 \times 0.03 + 20 \times 0.06 \\ 10 \times 0.08 + 20 \times 0.05 + 50 \times 0.03 + 20 \times 0.06 \end{bmatrix} = \begin{bmatrix} 1.6 + 1.5 + 0.3 + 2.4 \\ 4.0 + 0.5 + 0.6 + 1.2 \\ 0.8 + 1.0 + 1.5 + 1.2 \end{bmatrix} = \begin{bmatrix} 5.8 \\ 6.3 \\ 4.5 \end{bmatrix}
\]
也就是说,客户A、B、C的季度预期收益分别为 5.8 万元、6.3 万元和 4.5 万元。
✅ 管理意义:矩阵乘法使得面对成百上千客户时,也能轻松、批量地计算投资预期回报;并可用于灵敏度分析、风险评估等高级分析。
四 矩阵其他乘法——内积和外积
4.1 矩阵内积
两个矩阵A、B对应分量乘积之和,结果为一个标量,记作<A,B>(与向量的内积/点积/数量积的定义相似),所以A、B的行数列数都应相同,\(<A,B>=tr(A^T*B)\)。例如:
\[A=\begin{bmatrix} a_{11}& a_{12} \\ a_{21} & a_{22} \end{bmatrix}B=\begin{bmatrix} b_{11}& b_{12} \\ b_{21} & b_{22} \end{bmatrix}
\]
则
\[ <A,B> =a_{11} b_{11}+a_{12}b_{12}+a_{21} b_{21}+a_{22} b_{22}
\]
4.2 Kronecker积(矩阵外积)
两个矩阵的 Kronecker 积分为右Kronecker 积和左 Kronecker 积。鉴于通常多采用右 Kronecker积,通常所说的 Kronecker 积多指右 Kronecker 积。
右 Kronecker 积定义: \(m \times n\) 矩阵$ A=[a_{1},\cdot\cdot\cdot,a_{n}]$ 和$ p \times q$ 矩阵\(B\) 的右 Kronecker 积记作
\[A⊗B
\]
,是一个$mp \times nq $矩阵
\[A⊗B=[a_{1}B,\cdot\cdot\cdot,a_{n}B] =[a_{ij}B]_{i=1,j=1}^{m,n}\\
\]
其中 \(a_{ij}B\)代表的不是一个标量,而是一个$ p\times q$ 矩阵。将上式展开如下图所示:
\[\begin{aligned}
& \left[
\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}\\
a_{31} & a_{32}
\end{array}
\right]
\otimes
\left[
\begin{array}{lll}
b_{11} & b_{12} & b_{13} \\
b_{21} & b_{22} & b_{23}
\end{array}
\right]
=
\left[
\begin{array}{llllll}
a_{11}b_{11} & a_{11}b_{12} & a_{11}b_{13} & a_{12}b_{11} & a_{12}b_{12} & a_{12}b_{13} \\
a_{11}b_{21} & a_{11}b_{22} & a_{11}b_{23} & a_{12}b_{21} & a_{12}b_{22} & a_{12}b_{23} \\
a_{21}b_{11} & a_{21}b_{12} & a_{21}b_{13} & a_{22}b_{11} & a_{22}b_{12} & a_{22}b_{13} \\
a_{21}b_{21} & a_{21}b_{22} & a_{21}b_{23} & a_{22}b_{21} & a_{22}b_{22} & a_{22}b_{23}\\
a_{31}b_{11} & a_{31}b_{12} & a_{31}b_{13} & a_{32}b_{11} & a_{32}b_{12} & a_{32}b_{13} \\
a_{31}b_{21} & a_{31}b_{22} & a_{31}b_{23} & a_{32}b_{21} & a_{32}b_{22} & a_{32}b_{23}
\end{array}
\right]
\end{aligned}
\]
\[\begin{aligned}& {\left[\begin{array}{ll}
1 & 2 \\
3 & 1
\end{array}\right] \otimes\left[\begin{array}{ll}
0 & 3 \\
2 & 1
\end{array}\right]=\left[\begin{array}{llll}
1 \cdot 0 & 1 \cdot 3 & 2 \cdot 0 & 2 \cdot 3 \\
1 \cdot 2 & 1 \cdot 1 & 2 \cdot 2 & 2 \cdot 1 \\
3 \cdot 0 & 3 \cdot 3 & 1 \cdot 0 & 1 \cdot 3 \\
3 \cdot 2 & 3 \cdot 1 & 1 \cdot 2 & 1 \cdot 1
\end{array}\right]=\left[\begin{array}{llll}
0 & 3 & 0 & 6 \\
2 & 1 & 4 & 2 \\
0 & 9 & 0 & 3 \\
6 & 3 & 2 & 1
\end{array}\right] }
\end{aligned}
\]
左Kronecker 积定义:
\[[A⊗B]_{left}=[Ab_{1},\cdot\cdot\cdot,Ab_{q}]=[b_{ij}A]_{i=1,j=1}^{p,q}
\]
如果我们用右Kronecker 积的形式来表示左 Kronecker 积,则
\[[A⊗B]_{left}=B \otimes A
\]
这也是为什么通常我们所说的Kronecker 积是指右 Kronecker 积。该积也称直积或张量积。
在信号处理中,Kronecker积有几个重要的应用方面:
多维信号的混叠矩阵构建: 当处理多维信号时,通常需要将其表示为一个向量形式以方便处理。然而,多维信号的混叠问题会导致信号在转换为向量时失去原有的结构信息。为了解决这个问题,可以使用Kronecker积构建混叠矩阵。假设有多个信号,每个信号都是一个二维矩阵,将它们通过Kronecker积叠加到一个大的混叠矩阵中,使得原始信号的结构在向量化后能够被保留。
滤波器设计: 在数字信号处理中,滤波器是一种常用的工具,用于去除噪声、提取特定频率成分等。Kronecker积可以用于设计多维信号的滤波器。通过将滤波器的参数表示为Kronecker积形式,可以更灵活地设计各种类型的滤波器,并且可以方便地应用于不同维度的信号。
卷积编码器设计: 卷积编码是一种常见的信号编码方法,通常用于通信系统中的误码控制。Kronecker积可以用于设计卷积编码器的生成矩阵。通过使用Kronecker积构建生成矩阵,可以设计出具有良好性能的卷积编码器,同时能够适应不同信号空间的需求。
4.3 Hadamard积
\(m\times n\) 矩阵 $A=[a_{ij}] $和 \(B=[b_{ij}]\) 的 Hadamard 积记作$ A∗B$,它仍然是一个 \(m \times n\) 矩阵,其元素定义为两个矩阵对应元素的乘积。
与矩阵的直和运算类似,矩阵直和定义为两个矩阵矩阵对应元素的和。但要注意,Hadamard 积并不称为直积,直积是我们上面看到的 Kronecker 积。
Hadamard 积公式表示如下:
\[(A∗B)_{ij}=a_{ij}*b_{ij}
\]
\[\begin{aligned}
& \left(\begin{array}{lll}
1 & 3 & 2 \\
1 & 0 & 0 \\
1 & 2 & 2
\end{array}\right) *\left(\begin{array}{lll}
0 & 0 & 2 \\
7 & 5 & 0 \\
2 & 1 & 1
\end{array}\right)=\left(\begin{array}{cccc}
1 \cdot 0 & 3 \cdot 0 & 2 \cdot 2 \\
1 \cdot 7 & 0 \cdot 5 & 0 \cdot 0 \\
1 \cdot 2 & 2 \cdot 1 & 2 \cdot 1
\end{array}\right)=\left(\begin{array}{lll}
0 & 0 & 4 \\
7 & 0 & 0 \\
2 & 2 & 2
\end{array}\right)
\end{aligned}
\]
矩阵的Hadamard 积在有损压缩算法(例如JPEG)中被使用。
| 内核(kernel,即3x3矩阵) |
卷积神经网络 |
 |
 |
总结
矩阵是天才的数学语言符号。线性代数是一种人为设计的领域特定语言(DSL),它建立了一套模型并通过符号系统完成语法和语义的映射,实际上,向量、矩阵、运算规则的语法和语义都是人为的设计,这和一门语言中的各种概念性质相同,它是一种创造,但是前提是必须满足语言契约。可能有人对把线性代数当成一门DSL不放心,我给你一个矩阵,你就把我的图形旋转了60度沿x轴拉伸了2倍,我都不知道你“底 层”是怎么做!建立新模型肯定依赖于现有的模型,但这是建模的手段而不是目的,任何一种新模型的目的都为了更简单地分析和解决某一类问题。线性代数在建立的时候,它的各种概念和运算规则依赖于初等数学的知识,但是一旦建立起来这层抽象模型之后,我们就应该习惯于直接利用高层次的抽象模型去分析和解决问题。
参考资料
1.矩阵乘法核心思想(5):内积与外积
2.矩阵的乘法
3. 矩阵基础 | 矩阵特殊乘积运算










 浙公网安备 33010602011771号
浙公网安备 33010602011771号