数据挖掘神经网络—R实现

生物神经网络主要是指人脑的神经网络，它是人工神经网络的技术原型。人脑是人类思维的物质基础，思维的功能定位在大脑皮层，后者含有大约10^11个神经元，每个神经元又通过神经突触与大约103个其它神经元相连，形成一个高度复杂高度灵活的动态网络。作为一门学科，生物神经网络主要研究人脑神经网络的结构、功能及其工作机制，意在探索人脑思维和智能活动的规律。人工神经网络是生物神经网络在某种简化意义下的技术复现，作为一门学科，它的主要任务是根据生物神经网络的原理和实际应用的需要建造实用的人工神经网络模型，设计相应的学习算法，模拟人脑的某种智能活动，然后在技术上实现出来用以解决实际问题。因此，生物神经网络主要研究智能的机理；人工神经网络主要研究智能机理的实现，两者相辅相成。

一、神经网络概述

人工神经网络以并行分布的处理能力、高容错性、智能化和自学习等能力为特征，将信息的加工和存储结合在一起，以其独特的知识表示方式和智能化的自适应学习能力，引起各学科领域的关注。它实际上是一个有大量简单元件相互连接而成的复杂网络，具有高度的非线性，能够进行复杂的逻辑操作和非线性关系实现的系统。后来随着人们对感知机兴趣的衰退，神经网络的研究沉寂了相当长的时间。80年代初期，模拟与数字混合的超大规模集成电路制作技术提高到新的水平，完全付诸实用化，此外，数字计算机的发展在若干应用领域遇到困难。这一背景预示，向人工神经网络寻求出路的时机已经成熟。美国的物理学家Hopfield于1982年和1984年在美国科学院院刊上发表了两篇关于人工神经网络研究的论文，引起了巨大的反响。人们重新认识到神经网络的威力以及付诸应用的现实性。随即，一大批学者和研究人员围绕着 Hopfield提出的方法展开了进一步的工作，形成了80年代中期以来人工神经网络的研究热潮。

1. 神经网络算法思想

在生物神经网络中，每个神经元的树突接受来自之前多个神经元输出的电信号，将其组合成更强的信号。如果组合后的信号足够强，超过阀值，这个神经元就会被激活并且也会发射信号，信号则会沿着轴突到达这个神经元的终端，再传递给接下来更多的神经元的树突，如下图所示。

仿照生物神经网络，构建多层人工神经网络，每一层的人工神经元都与其前后层的神经元相互连接，如下图所示。在每个连接上显示了相关的连接权重，较小的权重将弱化信号，而较大的权重将放大信号。对于神经网络中的单个神经元而言， 人工神经元的前半端（图3中红色虚线框）相当于生物神经元的树突，是输入端，用来接受多个神经元输出的信号并进行组合；人工神经元的后半端（图3中绿色虚线框）相当于生物神经元的轴突，是输出端，用来输出信号给接下来更多的神经元；前后端中间的分界线是激活函数，相当于生物神经元的阀值函数，用来对输入的组合信号判断是否达到阀值，如果达到阀值则该神经元激活，向输出端输出信号，否则抑制信号，不进行输出。

因此，神经网络的基本原理是将神经网络的输出值y与训练样本中标定的真实输出值进行比较，计算出输出误差，之后再使用这个误差值来指导前后两层中每两个神经元之间连接权重的调整，进而逐步改善神经网络的输出值，直至与训练样本的真实输出值之间的误差达到很小，在设定的可容忍范围内为止。可以看出，前后两层中每两个神经元之间的连接权重就是神经网络需要进行学习的内容，对这些连接权重持续进行优化，才能使神经网络的输出越来越好，达到我们满意的结果。

如上图所示，输入信号从第一层（也就是输入层）进入神经网络后，不管自输入层以后到底有多少层，都可以使用以下两步来计算经过各层后的输出信号：一是利用连接权重来调节从前一层中各神经元输入的信号并进行组合；二是对组合之后的信号应用激活函数，生成该层的输出信号。而对于第一层的输入层而言，仅仅表示输入层中每个神经元的输入而已，对输入层中每个神经元不使用激活函数。

2. 人工神经元模型

人工神经元是人工神经网络的基本单元。模拟生物神经元，人工神经元有1个或者多个输入（模拟多个树突或者多个神经元向该神经元传递神经冲动）；对输入进行加权求和（模拟细胞体将神经信号进行积累和树突强度不同）；对输入之和使用激活函数计算活性值（模拟细胞体产生兴奋或者抑制）；输出活性值并传递到下一个人工神经元（模拟生物神经元通过轴突将神经冲动输入到下一个神经元）。

图中人工神经元有\(n\)个输入 \(x_{1}\),\(x_{2}\),...,\(x_{n}\)，是从其它神经元传入的输入信号，\(W_{i1}\)-\(W_{in}\)分别是传入信号的权重，\(\theta\)表示阈值，或称为偏置（bias），偏置的设置是为了正确分类样本，是模型中一个重要的参数。神经元综合的输入信号和偏置（符号为-1~1）相加之后产生当前神经元最终的处理信号net，该信号称为净激活或净激励（net activation），激活信号作为上图中圆圈的右半部分\(f(*)\)函数的输入，即\(f(net)\)； \(f\)称为激活函数或激励函数（Activation Function），激活函数的主要作用是加入非线性因素，解决线性模型的表达、分类能力不足的问题。上图中\(y_i\)是当前神经元的输出。

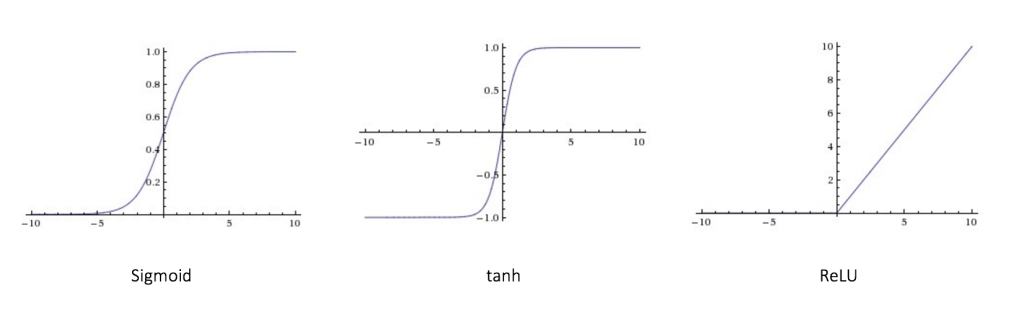
一些比较常见的激活函数。

Sigmoid

输出范围是[0,1]

[公式]

tanh

输出范围是[-1,1]

[公式]

ReLU

[公式]

激活函数的图像

3. 神经网络的计算步骤

三层神经网络的代码框架

第一步，建立神经网络模型：设定输入层、中间层和输出层节点的数目，设置学习率的大小， 随机初始化输入层和中间层以及中间层和输出层之间的连接权重矩阵。
第二步，训练神经网络：训练函数——给定训练集样本后，正向计算输出值并根据样本标定的真实值算出误差值，再反向传播误差算出中间层的误差值，最后计算出误差函数相对于连接权重的斜率并利用梯度下降法更新输入层和中间层以及中间层和输出层之间的连接权重矩阵。
第三步，泛化外推预测：应用神经网络,计算出自输入层以后每一层神经网络的正向输出值并输出神经网络的最终值。

4. B-P神经网络

如下图所示，这个神经网络分为3个网络层，分别是输入层，隐藏层和输出层，每个网络层都包含有多个神经元，每个神经元都会跟相邻的前一个层的神经元有连接，这些连接其实也是该神经元的输入。根据神经元所在层的不同，前向神经网络的神经元也分为三种，分别为：

3.1输入神经元

位于输入层，主要是传递来自外界的信息进入神经网络中，比如图片信息，文本信息等，这些神经元不需要执行任何计算，只是作为传递信息，或者说是数据进入隐藏层。

3.2隐藏神经元

位于隐藏层，隐藏层的神经元不与外界有直接的连接，它都是通过前面的输入层和后面的输出层与外界有间接的联系，因此称之为隐藏层，上图只是有1个网络层，但实际上隐藏层的数量是可以有很多的，远多于1个，当然也可以没有，那就是只有输入层和输出层的情况了。隐藏层的神经元会执行计算，将输入层的输入信息通过计算进行转换，然后输出到输出层。

3.3输出神经元

位于输出层，输出神经元就是将来自隐藏层的信息输出到外界中，也就是输出最终的结果，如分类结果等。
前向网络中，信息是从输入层传递到输出层，只有前向这一个方向，没有反向传播，也不会循环（不同于RNN，它的神经元间的连接形成了一个循环）。

二、 BP神经网络的R实现

1. 神经网络的数据结构

神经网络用到的数据结构如下图所示。

   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1           5.1         3.5          1.4         0.2  setosa
2           4.9         3.0          1.4         0.2  setosa
3           4.7         3.2          1.3         0.2  setosa
4           4.6         3.1          1.5         0.2  setosa
5           5.0         3.6          1.4         0.2  setosa
6           5.4         3.9          1.7         0.4  setosa
7           4.6         3.4          1.4         0.3  setosa
8           5.0         3.4          1.5         0.2  setosa
9           4.4         2.9          1.4         0.2  setosa
10          4.9         3.1          1.5         0.1  setosa

2. R处理程序

rm(list = ls())
install.packages("neuralnet")
library(neuralnet)            #加载神经网络计算包

data("iris")
ind<-sample(2,nrow(iris),replace = T,prob = c(0.7,0.3))
trainset<-iris[ind==1,]          #训练样本
testset<-iris[ind==2,]           #测试样本 

#建构神经网络模型
trainset$setosa<-trainset$Species=="setosa"
trainset$virginica<-trainset$Species=="virginica"
trainset$versicolor<-trainset$Species=="versicolor"     #训练数据处理

attach(iris)
network<-neuralnet(versicolor+virginica+setosa~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,trainset,hidden = 3)  #神经网络建模

3. 计算结果

plot(network)
network$result.matrix
head(network$generalized.weights[[1]])


net.predict<-compute(network,testset[-5])$net.result
net.prediction<-c("versicolor","virginica","setosa")[apply(net.predict,1,which.max)]

predict.table<-table(testset$Species,net.prediction)
predict.table                                                #神经网络模型的评估

           net.prediction
             setosa versicolor virginica
  setosa         14          0         0
  versicolor      0         15         0
  virginica       0          2        14                     #神经网络模型的评估

4.泛化外推预测

{r setup, include=FALSE}
predict.table<-table(testset$Species,net.prediction)

三、总结

神经网络技术在模式识别与分类、识别滤波、自动控制、预测等方面已展示了其非凡的优越性。神经网络的结构由一个输入层、若干个中间隐含层和一个输出层组成。神经网络分析法通过不断学习，能够从未知模式的大量的复杂数据中发现其规律。神经网络方法克服了传统分析过程的复杂性及选择适当模型函数形式的困难，它是一种自然的非线性建模过程，毋需分清存在何种非线性关系，给建模与分析带来极大的方便。2021年6月9日，英国《自然》杂志发表一项人工智能突破性成就，美国科学家团队报告机器学习工具已可以极大地加速计算机芯片设计。研究显示，该方法能给出可行的芯片设计，且芯片性能不亚于人类工程师的设计，而整个设计过程只要几个小时，而不是几个月，这为今后的每一代计算机芯片设计节省数千小时的人力。这种方法已经被谷歌用来设计下一代人工智能计算机系统。研究团队将芯片布局规划设计成一个强化学习问题，并开发了一种能给出可行芯片设计的神经网络。

参考文献

1.(神经网络的基本原理)[https://zhuanlan.zhihu.com/p/68624851]
2.(第五章 人工神经网络)[https://blog.csdn.net/AuroraLLL/article/details/122211469]
3.(神经网络计算过程详细分析)[https://zhuanlan.zhihu.com/p/350050035]
4.(神经网络分类总结)[https://blog.csdn.net/qq_36623595/article/details/115580918]

posted @ 2022-05-02 18:19  郝hai  阅读(358)  评论(0)  编辑  收藏  举报