深度学习系列1-逻辑回归分类
目录
1. 基本框架理论
1.1. Forward propagation
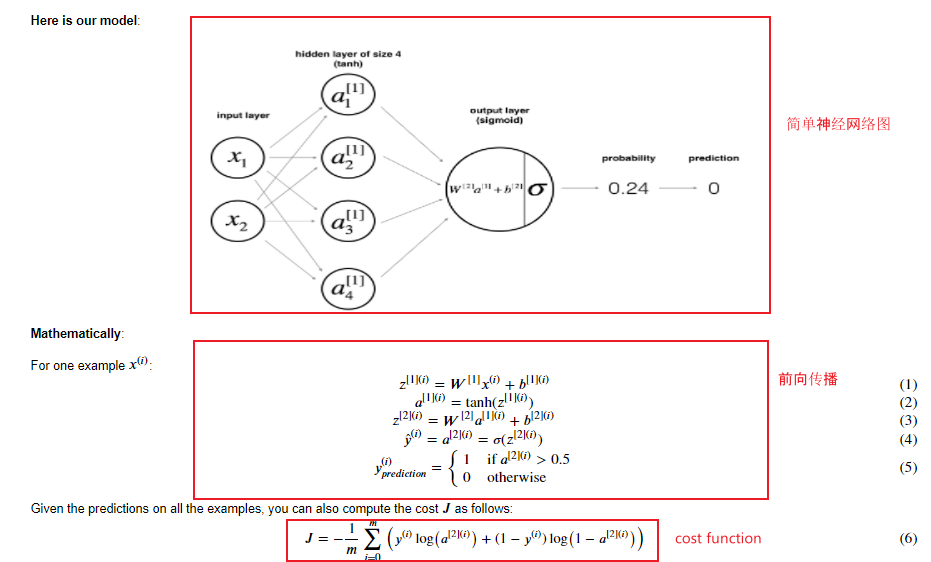
1.2. Backward Propagation

2. 代码流程
前提:
- 输入的X维度是(No.feature,No.sample)
- 输出的Y维度是(1,No.sample)
2.1. 初始化参数
- weight用
np.random.randn(a,b)*0.01来初始化 - bias用
np.zeros((a,b))来初始化
def initiate_parameter(self,n_x,n_h,n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
params -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
np.random.seed(2)
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros((n_y,1))
parameters = {"W1": W1,
"b1":b1,
"W2":W2,
"b2":b2}
return parameters
2.2. 前向传播
- 隐层使用
tanh,输出层使用sigmoid - 计算激活函数
def sigmoid(Z):
A = 1/(1+np.exp(-Z))
cache = Z
return A, cache
def relu(Z):
A = np.maximum(0,Z)
cache = Z
return A, cache
- 构造单个前向函数
def linear_forward(self, A_prev, W, b):
Z = np.dot(W,A_prev) + b
cache = (A_prev, W, b)
return Z, cache
- 前向传播激活函数选择器
def linear_activation_forward(self,A_prev, W, b, activation="relu"):
"""
Implement the forward propagation for the LINEAR->ACTIVATION layer
Arguments:
A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
b -- bias vector, numpy array of shape (size of the current layer, 1)
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
A -- the output of the activation function, also called the post-activation value
cache -- a python dictionary containing "linear_cache" and "activation_cache";
stored for computing the backward pass efficiently
"""
if activation == "sigmoid":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
if activation == "relu":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
cache = (linear_cache, activation_cache)
return A, cache
2.3. 计算损失函数
- 计算网络算出来的y值和真实y的差距
def compute_cost(AL, Y):
"""
Implement the cost function defined by equation (7).
Arguments:
AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)
Returns:
cost -- cross-entropy cost
"""
m = Y.shape[1]
# Compute loss from aL and y.
cost = (1./m) * (-np.dot(Y,np.log(AL).T) - np.dot(1-Y, np.log(1-AL).T))
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
assert(cost.shape == ())
return cost
2.4. 反向传播:梯度下降
- 计算出激活函数的导数
def relu_backward(dA, cache):
Z = cache
dZ = np.array(dA, copy=True) # just converting dz to a correct object.
# When z <= 0, you should set dz to 0 as well.
dZ[Z <= 0] = 0
assert (dZ.shape == Z.shape)
return dZ
def sigmoid_backward(dA, cache):
Z = cache
s = 1/(1+np.exp(-Z))
dZ = dA * s * (1-s)
assert (dZ.shape == Z.shape)
return dZ
- 构造单个反向传播的函数
def linear_backward(dZ, cache):
"""
Implement the linear portion of backward propagation for a single layer (layer l)
Arguments:
dZ -- Gradient of the cost with respect to the linear output (of current layer l)
cache -- tuple of values (A_prev, W, b) coming from the forward propagation in the current layer
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
A_prev, W, b = cache
m = A_prev.shape[1]
dW = 1./m * np.dot(dZ,A_prev.T)
db = 1./m * np.sum(dZ, axis = 1, keepdims = True)
dA_prev = np.dot(W.T,dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
- 设置反向传播的激活函数选择器
def linear_activation_backward(dA, cache, activation):
"""
Implement the backward propagation for the LINEAR->ACTIVATION layer.
Arguments:
dA -- post-activation gradient for current layer l
cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
linear_cache, activation_cache = cache
if activation == "relu":
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
return dA_prev, dW, db
2.5 更新参数
def update_parameters(parameters, grads, learning_rate):
"""
Update parameters using gradient descent
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients, output of L_model_backward
Returns:
parameters -- python dictionary containing your updated parameters
parameters["W" + str(l)] = ...
parameters["b" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural network
# Update rule for each parameter. Use a for loop.
for l in range(L):
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]
return parameters
3.6. 预测
def predict(X, y, parameters):
"""
This function is used to predict the results of a L-layer neural network.
Arguments:
X -- data set of examples you would like to label
parameters -- parameters of the trained model
Returns:
p -- predictions for the given dataset X
"""
m = X.shape[1]
n = len(parameters) // 2 # number of layers in the neural network
p = np.zeros((1,m))
# Forward propagation
probas, caches = L_model_forward(X, parameters)
# convert probas to 0/1 predictions
for i in range(0, probas.shape[1]):
if probas[0,i] > 0.5:
p[0,i] = 1
else:
p[0,i] = 0
#print results
#print ("predictions: " + str(p))
#print ("true labels: " + str(y))
print("Accuracy: " + str(np.sum((p == y)/m)))
return p
3. 应用
3.1. 构建一个两层神经网络
Question: Use the helper functions you have implemented in the previous assignment to build a 2-layer neural network with the following structure: LINEAR -> RELU -> LINEAR -> SIGMOID. The functions you may need and their inputs are:
def initialize_parameters(n_x, n_h, n_y):
...
return parameters
def linear_activation_forward(A_prev, W, b, activation):
...
return A, cache
def compute_cost(AL, Y):
...
return cost
def linear_activation_backward(dA, cache, activation):
...
return dA_prev, dW, db
def update_parameters(parameters, grads, learning_rate):
...
return parameters
- 完全的代码是
# GRADED FUNCTION: two_layer_model
def two_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
"""
Implements a two-layer neural network: LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (n_x, number of examples)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
layers_dims -- dimensions of the layers (n_x, n_h, n_y)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- If set to True, this will print the cost every 100 iterations
Returns:
parameters -- a dictionary containing W1, W2, b1, and b2
"""
np.random.seed(1)
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
(n_x, n_h, n_y) = layers_dims
# Initialize parameters dictionary, by calling one of the functions you'd previously implemented
### START CODE HERE ### (≈ 1 line of code)
parameters = initialize_parameters(n_x, n_h, n_y)
### END CODE HERE ###
# Get W1, b1, W2 and b2 from the dictionary parameters.
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> SIGMOID. Inputs: "X, W1, b1". Output: "A1, cache1, A2, cache2".
### START CODE HERE ### (≈ 2 lines of code)
A1, cache1 = linear_activation_forward(X, W1, b1, "relu")
A2, cache2 = linear_activation_forward(A1, W2, b2, "sigmoid")
### END CODE HERE ###
# Compute cost
### START CODE HERE ### (≈ 1 line of code)
cost = compute_cost(A2, Y)
### END CODE HERE ###
# Initializing backward propagation
dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
# Backward propagation. Inputs: "dA2, cache2, cache1". Outputs: "dA1, dW2, db2; also dA0 (not used), dW1, db1".
### START CODE HERE ### (≈ 2 lines of code)
dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
### END CODE HERE ###
# Set grads['dWl'] to dW1, grads['db1'] to db1, grads['dW2'] to dW2, grads['db2'] to db2
grads['dW1'] = dW1
grads['db1'] = db1
grads['dW2'] = dW2
grads['db2'] = db2
# Update parameters.
### START CODE HERE ### (approx. 1 line of code)
parameters = update_parameters(parameters, grads, learning_rate)
### END CODE HERE ###
# Retrieve W1, b1, W2, b2 from parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
3.2. 构建一个N层的深度神经网络
Question: Use the helper functions you have implemented previously to build an \(L\)-layer neural network with the following structure: [LINEAR -> RELU]\(\times\)(L-1) -> LINEAR -> SIGMOID. The functions you may need and their inputs are:
def initialize_parameters_deep(layer_dims):
...
return parameters
def L_model_forward(X, parameters):
...
return AL, caches
def compute_cost(AL, Y): # same to above
...
return cost
def L_model_backward(AL, Y, caches): #
...
return grads
def update_parameters(parameters, grads, learning_rate): # same to above
...
return parameters
DNN参数初始化
def initialize_parameters_deep(layer_dims):
"""
Arguments:
layer_dims -- python array (list) containing the dimensions of each layer in our network
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
bl -- bias vector of shape (layer_dims[l], 1)
"""
np.random.seed(1)
parameters = {}
L = len(layer_dims) # number of layers in the network
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) / np.sqrt(layer_dims[l-1]) #*0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parameters
DNN 前向传播
def L_model_forward(X, parameters):
"""
Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation
Arguments:
X -- data, numpy array of shape (input size, number of examples)
parameters -- output of initialize_parameters_deep()
Returns:
AL -- last post-activation value
caches -- list of caches containing:
every cache of linear_relu_forward() (there are L-1 of them, indexed from 0 to L-2)
the cache of linear_sigmoid_forward() (there is one, indexed L-1)
"""
caches = []
A = X
L = len(parameters) // 2 # number of layers in the neural network
# Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
for l in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation = "relu")
caches.append(cache)
# Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation = "sigmoid")
caches.append(cache)
assert(AL.shape == (1,X.shape[1]))
return AL, caches
DNN 损失函数
和之前的一样
DNN 后向传播
def L_model_backward(AL, Y, caches):
"""
Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group
Arguments:
AL -- probability vector, output of the forward propagation (L_model_forward())
Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
caches -- list of caches containing:
every cache of linear_activation_forward() with "relu" (there are (L-1) or them, indexes from 0 to L-2)
the cache of linear_activation_forward() with "sigmoid" (there is one, index L-1)
Returns:
grads -- A dictionary with the gradients
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
# Initializing the backpropagation
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
# Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "AL, Y, caches". Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
current_cache = caches[L-1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation = "sigmoid")
for l in reversed(range(L-1)):
# lth layer: (RELU -> LINEAR) gradients.
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, activation = "relu")
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
DNN 参数更新
和之前的一样



