有向无环图
Time Limit: 5 Sec Memory Limit: 128 Mb Submitted: 751 Solved: 313
Description
Bobo 有一个 n 个点，m 条边的有向无环图（即对于任意点 v，不存在从点 v 开始、点 v 结束的路径）。
为了方便，点用 1,2,…,n 编号。 设 count(x,y) 表示点 x 到点 y 不同的路径数量（规定 count(x,x)=0），Bobo 想知道
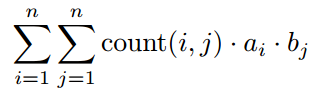
除以 (109+7) 的余数。
其中，ai,bj 是给定的数列。
Input
输入包含不超过 15 组数据。
每组数据的第一行包含两个整数 n,m (1≤n,m≤105).
接下来 n 行的第 i 行包含两个整数 ai,bi (0≤ai,bi≤109).
最后 m 行的第 i 行包含两个整数 ui,vi，代表一条从点 ui 到 vi 的边 (1≤ui,vi≤n)。
Output
对于每组数据，输出一个整数表示要求的值。
Sample Input
3 3
1 1
1 1
1 1
1 2
1 3
2 3
2 2
1 0
0 2
1 2
1 2
2 1
500000000 0
0 500000000
1 2
Sample Output
4
4
250000014
Hint
Source
湖南省第十二届大学生计算机程序设计竞
//叉姐还是厉害啊，水题都比较考思维，有向无环图，要是把入度为零的点提起来，其实挺像树的。。。(图论渣渣的想法)
先小范围想想，很简单，用该点的 a[i] 乘所有子节点 b[i] 即可，再把子节点的所有所有 b[i] 累加
这样，又可以把这个当做新节点，同上处理
1 # include <cstdio> 2 # include <cstring> 3 # include <cstdlib> 4 # include <iostream> 5 # include <vector> 6 # include <queue> 7 # include <stack> 8 # include <map> 9 # include <bitset> 10 # include <sstream> 11 # include <set> 12 # include <cmath> 13 # include <algorithm> 14 #pragma comment(linker,"/STACK:102400000,102400000") 15 using namespace std; 16 #define LL long long 17 #define lowbit(x) ((x)&(-x)) 18 #define PI acos(-1.0) 19 #define INF 0x3f3f3f3f 20 #define eps 1e-8 21 #define MOD 1000000007 22 23 inline int scan() { 24 int x=0,f=1; char ch=getchar(); 25 while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();} 26 while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();} 27 return x*f; 28 } 29 inline void Out(int a) { 30 if(a<0) {putchar('-'); a=-a;} 31 if(a>=10) Out(a/10); 32 putchar(a%10+'0'); 33 } 34 #define MX 100005 35 /**************************/ 36 int n,m; 37 LL ans; 38 int a[MX]; 39 int b[MX]; 40 vector<int> G[MX]; 41 bool vis[MX]; 42 int w[MX]; 43 44 void dfs(int x) 45 { 46 vis[x]=1; 47 w[x]=b[x]; 48 for (int i=0;i<G[x].size();i++) 49 { 50 if (!vis[G[x][i]]) dfs(G[x][i]); 51 52 w[x]= (w[x] + w[G[x][i]])%MOD; 53 ans = ((ans + (LL)a[x]*w[G[x][i]])%MOD)%MOD; 54 } 55 } 56 57 int main() 58 { 59 while (scanf("%d%d",&n,&m)!=EOF) 60 { 61 for (int i=1;i<=n;i++) 62 { 63 a[i] = scan(); 64 b[i] = scan(); 65 } 66 for (int i=1;i<=m;i++) G[i].clear(); 67 for (int i=1;i<=m;i++) 68 { 69 int u,v; 70 u = scan(); v = scan(); 71 G[u].push_back(v); 72 } 73 memset(vis,0,sizeof(vis)); 74 75 ans = 0; 76 for (int i=1;i<=n;i++) 77 { 78 if (!vis[i]) dfs(i); 79 } 80 printf("%lld\n",ans); 81 } 82 return 0; 83 }
