算法竞赛进阶指南0.2 递推与递归
目录
1. 实现指数型枚举 3
2. 递归实现组合型枚举 3
3. 递归实现排列型枚举 4
4. 费解的开关 5
5. Strange Towers of Hanoi 6
6. Sumdiv 8
7. 分型之城 10
递推与递归
1. 实现指数型枚举
从n个数中选任意多个数 并输出
#include <iostream>
using namespace std;
int n;
void dfs(int cur,int state){
if(cur==n){
for(int i=0;i<n;i++){
if(state >> i & 1)
cout<<i+1<<" ";
}
cout<<endl;
return;
}
dfs(cur+1,state);
dfs(cur+1,state | 1 << cur);
}
int main(){
cin>>n;
dfs(0,0);
return 0;
};
2. 递归实现组合型枚举
从n个数中选择m个 要求按字典序输出所有情况
#include <iostream>
using namespace std;
int n,m;
void dfs(int cur,int sum , int state){
if(sum + n - cur < m) return;
if(sum==m){
for(int i=0;i<n;i++){
if(state >> i & 1)
cout<< i+1 << ' ';
}
cout<<endl;
return;
}
if(cur==n) return;
dfs(cur+1, sum+1, state | 1<<cur); //要保证先选小的所以这条语句在前
dfs(cur+1,sum ,state);
}
int main(){
cin>>n>>m;
dfs(0,0,0);
return 0;
};
3. 递归实现排列型枚举
n个数的全排列
#include <iostream>
#include <vector>
using namespace std;
int n;
vector<int> v;
void dfs(int cur,int state){
if(cur==n){
for(auto x : v)
cout<< x <<' ';
cout<<endl;
return;
}
for(int i = 0; i < n; i ++ ){
if(!(state >> i & 1)){
v.push_back(i+1);
dfs(cur+1 , state | 1 << i);
v.pop_back();
}
}
}
int main(){
cin>>n;
dfs(0,0);
return 0;
}
4. 费解的开关
枚举第一行按的状态 一共32种状态(全不按 到全按)
对于每一种状态 按过第一行之后锁定第一行 如果要修改第一行的灯的状态
只能通过按下面一行的对应位置来更改
那么我们就要看第一行哪个位置是0
就通过更改第二行的这一列 使得第一行这个位置变为1
然后像处理第一行这样处理完倒数第二行
如果这种状态是可以的话 处理完倒数第二行后 最后一行应该是全1 否则不符合
(整体思想就是 确定第一行的状态 然后根据第一行的状态确定第二行的状态 然后确定第二行 根据第二行的状态确定第三行 以此类推 然后根据最后一行判断)
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
char Map[6][10];
int now[6][6];
void init(){
for(int i=0;i<5;i++)
for(int j=0;j<5;j++)
now[i][j] = Map[i][j]-'0';
}
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
void fun(int x,int y){
now[x][y] ^= 1;
for(int i=0;i<4;i++){
int nowx = x+dx[i],nowy = y+dy[i];
if(nowx>=0&&nowx<5&&nowy>=0&&nowy<5)
now[nowx][nowy]^=1;
}
}
int main(){
int T;
scanf("%d",&T);
while(T--){
for(int i=0;i<5;i++)
scanf("%s",Map[i]);
int ans = 0x3f3f3f3f;
for(int i=0;i<1<<5;i++) {
init();
int cnt = 0;
for (int j = 0; j < 5; j++) //处理第一行
if (i >> j & 1) {
cnt++;
fun(0,4-j);
}
int flag = 0;
for(int j=0 ; j<4 ; j++){ //根据当前行 操作后一行
if(flag) break;
for(int k=0;k<5;k++){
if(!now[j][k]){
cnt++;
if(cnt>6){
flag = 1;
break;
}
fun(j+1,k);
}
}
}
if(flag) continue;
for(int i=0;i<5;i++){
if(!now[4][i]){
flag = 1;
break;
}
}
if(flag) continue;
ans = min(ans,cnt);
}
if(ans==0x3f3f3f3f) printf("-1\n");
else printf("%d\n",ans);
}
return 0;
}
5. Strange Towers of Hanoi
要求输出四个塔 1~12个盘子分别最小需要几步
3个塔n个盘子的hanoi塔的步数 d[n] = d[n-1] * 2 + 1
4个塔n个盘子的hanoi塔的步数 f[n] = min( 2 * f[n-i] + d[i] , f[n] ) 【i从1到 n遍历】
5个塔n个盘子的hanoi塔的步数 five[n] = min( 2 * five[n-i] + f[i] , five[n] ) 【i从1到 n遍历】
........
#include <iostream>
#include <cstring>
#include <cstdlib>
using namespace std;
const int maxn = 15;
int d[maxn],f[maxn];
int main(){
d[1] = 1;
for(int i=2;i<=12;i++)
d[i] = 2 * d[i-1] + 1;
memset(f , 0x3f , sizeof f);
f[1] = 1;
for(int i=2;i<=12;i++)
for(int j=1;j<=i;j++)
f[i] =min( f[i] , f[i-j]*2 + d[j]);
for(int i=1;i<=12;i++)
cout<<f[i]<<endl;
return 0;
}
推广到 n个 盘子 m个塔的最小步数
类比只有三个柱子的汉诺塔, 设f[i][j]f[i][j]为有ii个盘子jj个柱子时的最少步数. 那么肯定是把一些上面盘子移动到某根不是jj的柱子上, 然后把剩下的盘子移动到jj, 然后再把上面的盘子移动到jj. 于是就有递推式f[i][j]=minf[k][j]∗2+f[i−k][j−1]f[i][j]=minf[k][j]∗2+f[i−k][j−1]
代码如下:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<climits>
using namespace std;
#define min(a,b) ((a)<(b))?(a):(b)
#define LL long long
#define N 65
int n,m;
LL dp[N][N];
int main()
{
scanf("%d%d",&n,&m); //n个盘子 m个塔
for(int i=0;i<N;++i)
for(int j=0;j<N;++j) dp[i][j]=LLONG_MAX;
dp[3][0]=0;
for(int i=1;i<=n;++i) dp[3][i]=dp[3][i-1]*2 + 1; //计算3塔的步数
for(int i=4;i<=m;++i) dp[i][0]=0,dp[i][1]=1; //预处理
for(int i=4;i<=m;++i) //i个塔
for(int j=2;j<=n;++j) //j个盘子
for(int k=1;k<j;++k) dp[i][j]=min(dp[i][j],dp[i][j-k]*2+dp[i-1][k]);
printf("%lld\n",dp[m][n]);
return 0;
}
6. Sumdiv
求的所有约数之和mod 9901
A = p1^k1 * p2^k2 * p3^k3 * ....... * pn^kn
A^B = p1^k1B * p2^k2B * ...... * pn^knB
A的因子个数 = (k1 + 1) * (k2 + 1) * .... * (kn + 1) =
A的约数之和
= (p1^0 + p1^1 + ... + p1^k1) * (p2^0 + p2^1 + ... + p2^k2 ) * ... * (pn^0 + pn^1 + ... +pn^kn )
=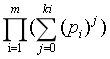
【原理很简单:将多项式展开 每一项为一个约数】
【对于A^B来说只需要将上式的ki 换成 ki * B即可】
对于每一个括号内的等比数列求和过程中,如果使用等比数列求和公式,需要做除法,但是mod操作对除没有分配律,不能直接操作。所以这里采用分治的方法
sum(p,c) = p^0 + P^1 + ... + p^k;
1) k为奇数,也就是有偶数项
sum(p,k) = (p^0 + p^1 + ... + p^(k/2) ) + (p^(k/2 + 1) + ... + p^k)
= (p^0 + p^1 + ... + p^(k/2) ) + (p^(k/2 + 1)) * (p^0 + p^1 + ... + p^(k/2) )
= [1+ p^(k/2 + 1)] * sum(p , k/2);
=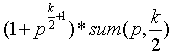
2) k为偶数,也就是有奇数项
Sum(p,k) =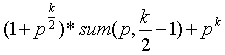
例 : 1) p^0 + p^1 + p^2 + p^3 + p^4 + p^5 (k = 5)
= p^0 + p^1 + p^2 + p^3*(p^0 + p^1 + p^2)
= (1 + p^3) * (p^0 + p^1 + p^2)
2) p^0 + p^1 + p^2 + p^3 + p^4 + p^5 + p^6 (k = 6)
= p^0 + p^1 + p^2 + p^3*(p^0 + p^1 + p^2) + p^61
= (1 + p^3) * (p^0 + p^1 + p^2) + p^6
#include <bits/stdc++.h>
using namespace std;
const int mod = 9901;
int qpow(int a, int b){
int res = 1;
a %= mod;
while(b){
if(b & 1){
res = res * a % mod;
}
a = a * a % mod;
b >>= 1;
}
return res % mod;
}
int sum(int p, int k){
if(k == 0) return 1;
if(k % 2 == 0) return (p % mod * sum(p , k - 1 ) + 1)%mod;
else return (1 + qpow(p , (k + 1) / 2)) % mod * sum(p , (k - 1) / 2) % mod;
}
int main(){
int A,B;
cin >> A >> B;
int ans = 1;
for(int i = 2 ; i <= A ; i++){
int cnt = 0;
while(A % i == 0){
cnt ++;
A /= i;
}
if(cnt){
ans = ans * sum(i , cnt * B) % mod;
}
}
if(!A) ans = 0;
cout << ans << endl;
return 0;
}
7. 分型之城
如何旋转一个坐标???
我们正常的坐标系:
(x,y)逆时针旋转θ角度:
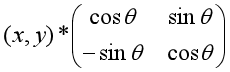
(x,y)顺时针旋转θ角度: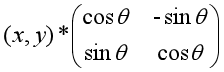
例如:顺时针旋转90° (1 , 2) -> ( 2 , -1 ) 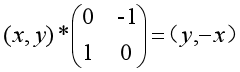
我们程序中常用的坐标系
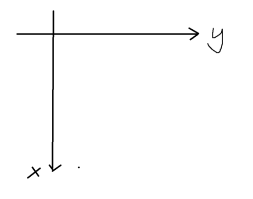
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
pll calc(ll n , ll m){
if(n == 0) return {0 , 0};
ll len = 1ll << (n - 1) , cnt = 1ll << (2 * n - 2);
// cnt为子问题点的数量 len代表等级为n时的图形长度的一半 用于平移坐标
auto pos = calc(n - 1 , m % cnt); //计算出m点在子问题中的位置
auto x = pos.first ;
auto y = pos.second;
auto z = m / cnt; // z = 0 1 2 3 分别代表 m在左上 右上 右下 左下
if(z == 0) return {y , x}; // 如果在第一部分的坐标变换 (旋转 -> 翻转 -> 平移)
else if(z == 1) return {x , y + len}; // 二
else if(z == 2) return {x + len , y + len}; //三
else return {2 * len - 1 - y , len - 1 - x}; //四
}
int main(){
int T;
scanf("%d",&T);
while(T--){
ll n , a, b;
scanf("%lld %lld %lld",&n , &a , &b);
auto ac = calc(n , a - 1);
auto bc = calc(n , b - 1);
double x = ac.first - bc.first , y = ac.second - bc.second;
printf("%.0lf\n", sqrt(x * x + y * y) * 10);
}
return 0;
}




