H - Second Large Rectangle 牛客第二场训练赛

H - Second Large Rectangle

 

 

 

 

 

题目分析 ：给你一个 N * M 的 01 矩阵 让你求出第二大的包含的全部都是”1”的矩阵的大小。 要求使用O(n^2)的方法找出第二大的矩阵

第二大的矩阵有两种情况：1.第二大的全1的矩阵  2.最大的矩阵的最大子矩阵

例：1.

0111

0111

1111

1111

1111

1111    它的答案就是16   

2.

111111

111111 它的答案是2*5的长方形 10

 

所以我们只需要构建一个答案序列，这个序列里有最大的矩形的大小和其最大的子矩阵的大小，然后将这个答案序列排序，第二大的就是答案

那么如何O(n^2)找最大的矩阵 ：

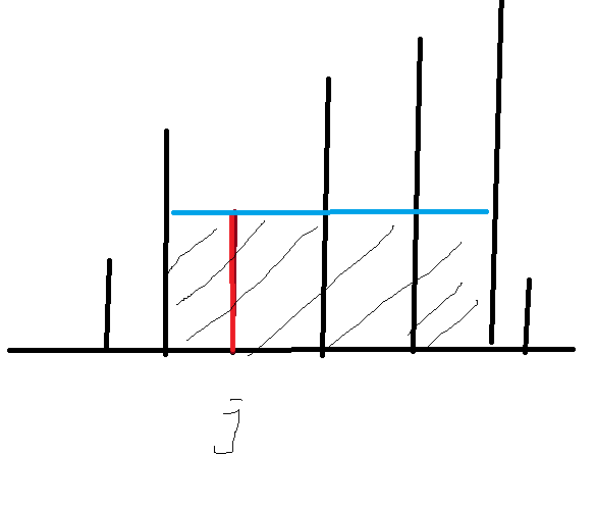
我们需要对遍历到的当前行的每个元素记录一个h[j],记录到这一行的这一列向上有多少个连续的1。然后记录一个l[j] , r[j]分别记录这个元素可以构成的矩形向左，向右最多可以到哪里。如图：高度为h[j]的矩形只能使用比它更高的。处理l[],r[]的复杂度为O(m)

 

 

 

代码:

#include <bits/stdc++.h>

using namespace std;
int c[1006][1006];
int l[1006],r[1006],h[1006];
int n,m;
int tot,p[4006000];
char str[1006];
set<pair<int,int> > s[1005];
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%s",str+1);
        for(int j=1;j<=m;j++){
            c[i][j]=str[j]-'0';
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){  //h[]
            if(c[i][j])h[j]++;
            else h[j]=0;
        }
        for(int j=1;j<=m;j++){ //l[]
            l[j]=j;
            while(l[j]>1&&h[j]<=h[l[j]-1]){
                l[j]=l[l[j]-1];
            }
        }
        for(int j=m;j>=1;j--){ //r[]
            r[j]=j;
            while(r[j]<m&&h[j]<=h[r[j]+1]){
                r[j]=r[r[j]+1];
            }
        }
        for(int j=1;j<=m;j++){
            if(s[i].find(make_pair(l[j],r[j]))==s[i].end()){
                p[++tot] = h[j]*(r[j]-l[j]+1);
                s[i].insert(make_pair(l[j],r[j]));
                if(r[j]-l[j]+1 > h[j]){  //如果矩形的横边 大于竖边 那么它最大的子矩阵是（横边-1）*竖边
                    p[++tot] = h[j] * (r[j] - l[j]);
                }
            }
        }
    }
    sort(p+1,p+1+tot);
    if(tot<=1)printf("0\n");
    else printf("%d\n",p[tot-1]);
    return 0;
}