轮回 dp

问题 G: 轮回

时间限制: 1 Sec  内存限制: 256 MB
提交: 46  解决: 19
[提交] [状态] [命题人:admin]

题目描述

孤独者的唯一救赎就是绝对而永恒的孤独。
北斗是一个喜欢玩游戏的女孩子。
今天她蒯来一部叫《CROSS†CHANNEL》的游戏准备玩，但是没玩几下就发现，这个游戏的章节并不是按照剧情发展顺序来排的！这太糟糕了！北斗准备把这个游戏的所有章节重新排序，然后再开始玩。现在北斗想要知道她最快还要多久才能玩到游戏，你能帮帮她吗？
这款游戏共有n个章节，按照剧情顺序以1~n标号。初始时这些章节是乱序的。
北斗可以执行如下两种操作。
1.选择一个章节并向前挪到任意位置。这一步需要消耗时间b。

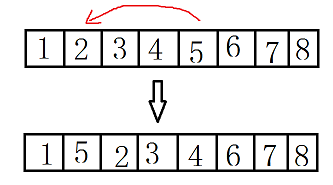
2.选择一个章节并向后挪到任意位置。这一步需要消耗时间a。

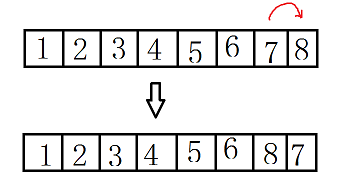
北斗的目标是把这些章节按照升序排好。

 

输入

第一行三个正整数n,a,b。
接下来一行是一个1~n的排列，表示初始时章节的顺序。

 

输出

输出一行一个数，表示把所有章节按顺序排好所花费的最少时间。

 

样例输入

复制样例数据

2 50 100 
2 1

样例输出

50

 

提示

 

题意：给你一段序列 你可以对其中的一个数进行两种操作 使得这个序列成为升序的

1.选一个数插到右边任意位置 花费a

2.选一个数插到左边任意位置 花费b

求最小的花费

 

思路 ：dp

dp[i][j] 表示遍历到 i 位置的数 最大没有移动的数为 j 的最小花费

这样可以确定当前比j小的都没有移动

当遇到比j大的数a[i] 有两种选择 ： 1. 移动它到它的最终位置 （一旦移动 最小花费一定会将它移动到它最终的位置）dp[i][j] = min(dp[i][j] , dp[i-1][j] + a)

　　　　　　　　　　　　　　　 2. 不移动它 这样当前的j就变成了a[i]   dp[i][a[i]] = min(dp[i][a[i]] , dp[i - 1][j]) 

当遇到比j小的数a[i] 只能将它移动到j前面 最大的没有移动的数还是j     dp[i][j] = min(dp[i][j] , dp[i - 1][j] + b)

#include <iostream>
#include <cstdio>
 
using namespace std;
typedef long long  ll;
const int maxn = 5005;
const long long inf = 1e18;
int n;
ll A, B, a[maxn],dp[maxn][maxn];
void init(){
    for(int i = 0 ; i <= n ; i++)
        for(int j = 0 ; j <= n ; j++)
            dp[i][j] = inf;
}
 
int main(){
    scanf("%d%d%d",&n,&A,&B);
    init();
    for(int i = 1 ; i <= n; i++)
        scanf("%d",&a[i]);
    dp[0][0] = 0;
    for(int i = 1 ; i <= n ; i++){
        for(int j = 0 ; j <= n ; j++){
            if(dp[i - 1][j]==inf) continue;
            if(a[i] > j){
                dp[i][a[i]] = min(dp[i][a[i]] , dp[i - 1][j]);//a[i] 不动
                dp[i][j] = min(dp[i][j] , dp[i - 1][j] + A);
            }else{
                dp[i][j] = min(dp[i][j] , dp[i - 1][j] + B);
            }
        }
    }
    ll ans = inf;
    for(int i = 0 ; i <= n ; i++){
        ans = min(dp[n][i],ans);
    }
    printf("%lld\n",ans);
    return 0;
}