矩阵快速幂【模板】

题目描述

给定一个n*n的矩阵A以及一个正整数k，计算S=A1+A2+A3+⋯+Ak

 

输入

输入只有一组测试数据。输入的第一行包括三个正整数 n，k，m。接下来的 n 行每行包括 n 个非负整数(在[0,32768)之间)，按照行优先的顺序输入矩阵 A 的元素。 

 

输出

输出 S 中每一个元素 mod(%)m 以后的值 

 

样例输入

1 998 1007
11

样例输出

360

提示

 

 

1.矩阵乘法

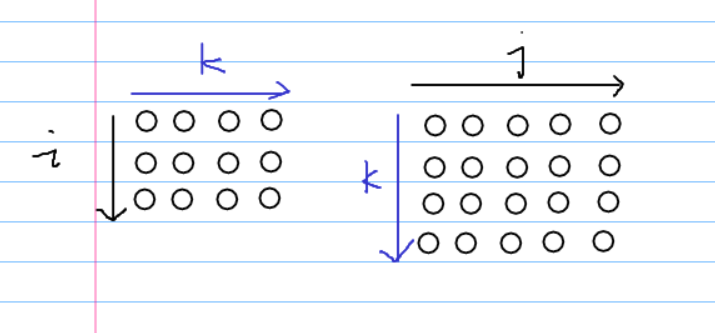
struct matrix{
    int mat[maxn][maxn];
}res,ans;

matrix mat_mul(matrix a,matrix b)
{
    matrix tmp={0};
    for(int i=1;i<=2*n;i++)
        for(int j=1;j<=n*2;j++)
            for(int k=1;k<=2*n;k++)
                tmp.mat[i][j] = (tmp.mat[i][j]%m+((a.mat[i][k]%m)*(b.mat[k][j]%m))%m)%m;
    return tmp;
}

2.快速幂

void qpow(int t)
{
    for(int i=1;i<=2*n;i++)
        for(int j=1;j<=2*n;j++)
        {
            if(i==j)
                ans.mat[i][j] = 1;
            else
                ans.mat[i][j] = 0;
        }
        
    while(t)
    {
        if(t&1)
        {
            ans = mat_mul(ans,res);
        }
        res = mat_mul(res,res);
        t>>=1;
    }
}

方法：构造矩阵 + 矩阵快速幂

有两种构造的矩阵的方法

1. （较为麻烦，最后注意减的是单位矩阵，不是全一矩阵，我在这错了好多发）

 

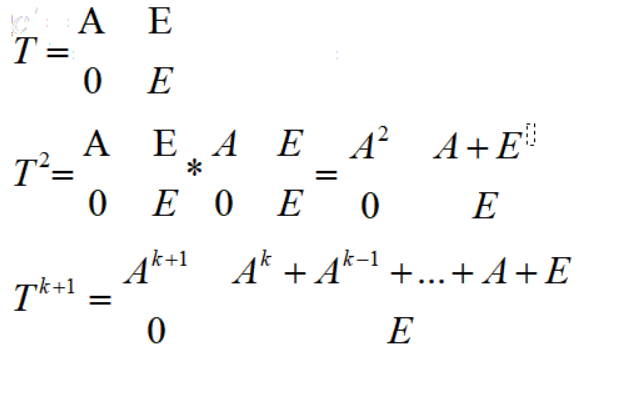
代码：

#include <bits/stdc++.h>
 
using namespace std;
 
int n,k,m;
const int maxn = 105;
struct matrix{
    int mat[maxn][maxn];
}res,ans;
 
matrix mat_mul(matrix a,matrix b)
{
    matrix tmp={0};
    for(int i=1;i<=2*n;i++)
        for(int j=1;j<=n*2;j++)
            for(int k=1;k<=2*n;k++)
                tmp.mat[i][j] = (tmp.mat[i][j]%m+((a.mat[i][k]%m)*(b.mat[k][j]%m))%m)%m;
    return tmp;
}
void qpow(int t)
{
    for(int i=1;i<=2*n;i++)
        for(int j=1;j<=2*n;j++)
        {
            if(i==j)
                ans.mat[i][j] = 1;
            else
                ans.mat[i][j] = 0;
        }
         
    while(t)
    {
        if(t&1)
        {
            ans = mat_mul(ans,res);
        }
        res = mat_mul(res,res);
        t>>=1;
    }
}
 
int main(){
    scanf("%d%d%d",&n,&k,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            scanf("%d",&res.mat[i][j]);
    for(int i=1;i<=n;i++)
        res.mat[i][i+n] = 1;
    for(int i=1+n;i<=2*n;i++)
        res.mat[i][i] = 1;
 
    qpow(k+1);
    for(int i=1;i<=n;i++)
        ans.mat[i][i+n] = (ans.mat[i][i+n]-1+m)%m;
    for(int i=1;i<=n;i++)
    {
        for(int j=1+n;j<=2*n;j++)
        {
            printf("%d ",ans.mat[i][j]);
        }
        printf("\n");
    }
    return 0;
} 

 

2.

 

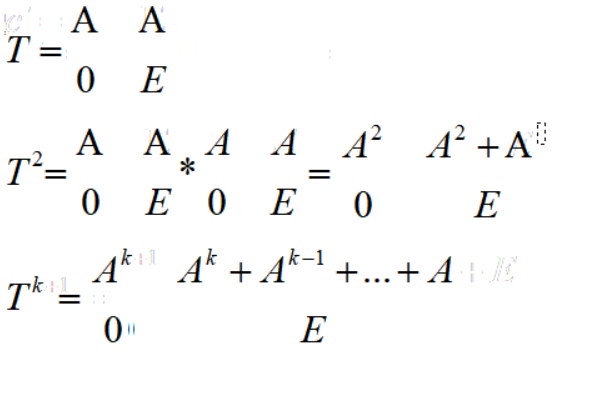
代码：

#include <bits/stdc++.h>
 
using namespace std;
 
int n,k,m;
const int maxn = 105;
struct matrix{
    int mat[maxn][maxn];
}res,ans;
 
matrix mat_mul(matrix a,matrix b)
{
    matrix tmp={0};
    for(int i=1;i<=2*n;i++)
        for(int j=1;j<=n*2;j++)
            for(int k=1;k<=2*n;k++)
                tmp.mat[i][j] = (tmp.mat[i][j]%m+((a.mat[i][k]%m)*(b.mat[k][j]%m))%m)%m;
    return tmp;
}
void qpow(int t)
{
    for(int i=1;i<=2*n;i++)
        for(int j=1;j<=2*n;j++)
        {
            if(i==j)
                ans.mat[i][j] = 1;
            else
                ans.mat[i][j] = 0;
        }
         
    while(t)
    {
        if(t&1)
        {
            ans = mat_mul(ans,res);
        }
        res = mat_mul(res,res);
        t>>=1;
    }
}
 
int main(){
    scanf("%d%d%d",&n,&k,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            scanf("%d",&res.mat[i][j]),res.mat[i][j+n]=res.mat[i][j]; 
    for(int i=1+n;i<=2*n;i++)
        res.mat[i][i] = 1;
    qpow(k);
    for(int i=1;i<=n;i++)
    {
        for(int j=1+n;j<=2*n;j++)
        {
            printf("%d ",ans.mat[i][j]);
        }
        printf("\n");
    }
    return 0;
}