哇塞 今天是数论专场呢 我要爆炸了
问题 B: 数论number
题目描述
给定正整数a,b,c和一个素数p,求

输入
一行,四个整数a,b,c,p(a,b,c,p≤2×109)
输出
一行,表示 的值。
的值。
 的值。
的值。样例输入
3 2 2 5
样例输出
1
应用:费马小定理
#include <bits/stdc++.h> using namespace std; typedef long long ll; ll poww(ll a,ll b,ll p) { ll ans=1,base = a; while(b!=0) { if(b&1!=0) { ans*=base; ans%=p; } base*=base; base%=p; b>>=1; } return ans; } int main() { ll a,b,c,p; while(cin>>a>>b>>c>>p) { // ll aa = a; // ll tmp = poww(a,b%(p-1)+(p-1),p); // tmp%=p; ll tmp = poww(b,c,p-1)+p-1; ll ans = poww(a,tmp,p); cout<<ans<<endl; // ll tt = pow(b,c); // ll ans2 = poww(aa,tt,p)%p; // cout<<" "<<ans2<<endl; } }
问题 C: 约数的平方和
题目描述
记f(n)为n的所有正约数的平方和,输入n和P,只需要输出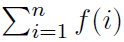 模P的值即可,保证P是素数。
模P的值即可,保证P是素数。
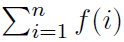 模P的值即可,保证P是素数。
模P的值即可,保证P是素数。
输入
一行,两个数n和P(n≤1012,P≤109)。
输出
一行,表示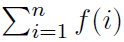 模P的值。
模P的值。
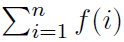 模P的值。
模P的值。
样例输入
3 20101009
样例输出
16
根据该公式:
其中,。
using namespace std; typedef long long ll; ll poww(ll a,ll b,ll p) { ll ans=1,base = a; while(b!=0) { if(b&1!=0) { ans*=base; ans%=p; } base*=base; base%=p; b>>=1; } return ans; } ll f(ll a,ll p) { ll now = 0; ll t1 = a%p; ll t2 = (a+1)%p; ll t3 = (2*a+1)%p; now = (((t1*t2)%p)*t3)%p; now= (now*poww(6,p-2,p))%p; return now; } int main() { ll n,p; scanf("%lld%lld",&n,&p); ll t1 = sqrt(n)+1; ll t2 = n/t1; ll ans = 0; for(ll i=1;i<=t2;i++) { ll tmp = ((i%p)*(i%p))%p; ll t3 = (((n/i)%p)*tmp)%p; ans += t3; ans%=p; } ll a1 = sqrt(n); for(ll i=1;i<=a1;i++) { ll a2 = (f(n/i,p)%p-f(n/(i+1),p)+p)%p; ans = (ans+((i%p)*(a2%p))%p)%p; } printf("%lld\n",ans%p); return 0; }
问题 B: 阿卡吃馅饼
题目描述
阿卡这天走在路上,被天上掉下来的一个巨大的馅饼给砸到了。他对自己的遭遇很疑惑,心想这次应该不是什么单纯的好运气了,一定是上天想要交给他一个任务!
阿卡果然猜对了。幻想世界的馅饼是一个可以膨胀的大馅饼,而它伸缩的幅度和我们平常容易见到的方式很不同,假设这个馅饼刚掉下来的时候有P单位大,这里保证(0<p<10)。那么膨胀一次,它就会变成lOP+P单位大,膨胀两次,就会变成lOOP+lOP+P单位大.以此类推。
举个例子,刚开始这个馅饼为1单位,膨胀一次它变成11,膨胀两次它变成111,膨胀三次变成llll。
阿卡想要把这个馅饼带回家,而家里一共有R个人,他为了公平起见觉得每个人吃到的馅饼单位数一定要一样而且一定要是个整数。
他想要让你帮忙计算最小的膨胀次数,是的膨胀完后的馅饼能平分给R个人,且每个人分到的是整数单位的馅饼。
阿卡果然猜对了。幻想世界的馅饼是一个可以膨胀的大馅饼,而它伸缩的幅度和我们平常容易见到的方式很不同,假设这个馅饼刚掉下来的时候有P单位大,这里保证(0<p<10)。那么膨胀一次,它就会变成lOP+P单位大,膨胀两次,就会变成lOOP+lOP+P单位大.以此类推。
举个例子,刚开始这个馅饼为1单位,膨胀一次它变成11,膨胀两次它变成111,膨胀三次变成llll。
阿卡想要把这个馅饼带回家,而家里一共有R个人,他为了公平起见觉得每个人吃到的馅饼单位数一定要一样而且一定要是个整数。
他想要让你帮忙计算最小的膨胀次数,是的膨胀完后的馅饼能平分给R个人,且每个人分到的是整数单位的馅饼。
输入
第一行一个数T,表示数据组数.
接下来T行,每行有两个数P,R。意义如题面中所示。
接下来T行,每行有两个数P,R。意义如题面中所示。
输出
输出T行,每行输出一组数据的答案。
输出每一组数据的最小膨胀次数,如果无论怎么膨胀都无法平分,在这组数据对应的输出中,输出一行“GG”(不包含引号)。
输出每一组数据的最小膨胀次数,如果无论怎么膨胀都无法平分,在这组数据对应的输出中,输出一行“GG”(不包含引号)。
样例输入
3
7 5
6 8
1 3
样例输出
GG
GG
2
提示
对于100%的数据,T≤103,R≤103
判断pp是否被r整除
p%r+(p%r*ksm(10,1,r)) //ksm为快速幂
#include <bits/stdc++.h> using namespace std; int poww(int a,int b,int p) { int ans=1,base = a; while(b!=0) { if(b&1!=0) { ans*=base; ans%=p; } base*=base; base%=p; b>>=1; } return ans; } int main() { int T; scanf("%d",&T); while(T--) { int p,r; scanf("%d%d",&p,&r); int pp = p; int flag = 0; int ans; for(int i=1;i<=1000;i++) { if(p%r==0) { flag = 1; ans = i-1; break; } int tmp = ((pp%r)*poww(10,i,r))%r; // cout<<tmp<<endl; p = (p%r+tmp%r)%r; } if(flag){ printf("%d\n",ans); } else { printf("GG\n"); } } return 0; }





