Cross-entropy loss多分类与二分类

看了好几次这个loss了，每次都容易忘，其他的博客还总是不合我的心意，所以打算记一下：

先说二值loss吧，即二分类问题

 

一、二分类

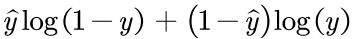
直接解释：

假设有两个类0，1。我们需要做的就是，使得属于0类的训练样本x经过网络M(x)之后的输出y尽可能的靠近0，相反则使得属于1类的训练样本x经过网络M(x)之后的输出y尽可能的靠近1。

分析上面这个公式，我们训练网络的直接手段当然是采用梯度下降法使得Loss函数越小越好(采用梯度上升则相反)。我们假设M(x)最后一层是有sigmoid()函数的，也就是输出y是在0到1之间的。

1、对于属于0类的x，标签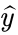应该是0，那么第一项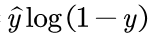就等于0了，第二项变为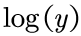，网络的输出y越靠近0，loss函数越小，符合我们的期望。 

2、对于属于1类的x，标签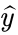应该是1，此时第二项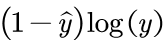就等于0了，第一项就变为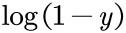，网络的输出y越靠近1，loss函数越小，符合我们的期望。

以上就是二分类问题了。

 

二、多分类

对于多分类问题，假设有6个类吧，Loss函数会变：

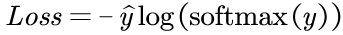
这个解释一下是这样的：

假设属于第三类的样本通过网络N(x)之后的输出是这样的：y=[0.23,0.12,0.4,0.05,0.09,0.11]

对应的标签当然是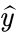：=[0,0,1,0,0,0,]

我们希望的是对应第三类的数字接近1，而其他类接近0。一个最简单的思想是输出向量y的每个值都和标签做差，这样loss越小肯定是效果越好。但是据前辈们的实践，没这个必要，我们只需要使得我们关心的这个类的对应位置靠近1即可，这样子还可以解决训练慢，overfitting等等一堆问题(有点类似dropout的思想，因为一些类的loss不用管的话，对应的神经元也就不用训练了)。这么一说，大家就都懂怎么“秀”了吧？

我们将输出与对应的标签乘起来，即上面那个公式。我们重写一遍如下：

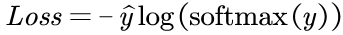
 这里的softmax() 函数一是可以让输出非负，二是可以让所有的输出是以概率的形式呈现出来，即所有的输出加起来等于1。如果不这样做，而用sigmoid()函数的话，就会出现即使目标类对应的位置等于0，但我们还是不能确定除了目标类之外的其他类是否接近0。

简单的例子，还是上面那个例子，简单一点说，如果输出的向量y，所有值加起来等于1，第三类接近1的话，那其他类肯定接近0了，这正是我们想要的效果。而如果向量y的所有值加起来不等于1，即使第三类位置上是1，你也不能确定其他类的位置上是不是还有比1更大的数，也就是不能确定第三类对应位置的概率是不是最大的。

softmax()配交叉熵，天长地久，欧耶！