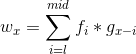洛谷4721 【模板】分治 FFT
传送门
久违的多项式全家桶= =+
分治NTT 用的就是cdq分治的思想 对于当前递归到的区间[l,r] 我们处理出[l,mid]对[mid+1,r]答案的贡献
然后分治递归求解就可以啦qwq
这个贡献是前一半卷积的答案加过去就可以啦
对于x的贡献
附代码。
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cmath>
#define ll long long
#define mdn 998244353
#define G 3
#define mxn 200010
using namespace std;
int ksm(int bs,int mi)
{
int ans=1;
while(mi)
{
if(mi&1) ans=(ll)ans*bs%mdn;
bs=(ll)bs*bs%mdn; mi>>=1;
}
return ans;
}
int rev[mxn],inv;
int init(int n)
{
int lim=1,l=0;
while(lim<n) lim<<=1,l++;
for(int i=1;i<lim;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
inv=ksm(lim,mdn-2);
return lim;
}
void NTT(int *a,int n,int f)
{
for(int i=0;i<n;i++) if(rev[i]>i) swap(a[rev[i]],a[i]);
for(int k=2;k<=n;k<<=1)
{
int Wn=ksm(G,(mdn-1)/k),mid=k>>1;
if(f) Wn=ksm(Wn,mdn-2);
for(int w=1,i=0;i<n;i+=k,w=1)
for(int j=0;j<mid;j++,w=(ll)w*Wn%mdn)
{
int x=a[i+j],y=(ll)w*a[i+mid+j]%mdn;
a[i+j]=(x+y)%mdn;
a[i+mid+j]=(x-y+mdn)%mdn;
}
}
if(f) for(int i=0;i<n;i++) a[i]=(ll)a[i]*inv%mdn;
}
int f[mxn],g[mxn],h[mxn],a[mxn],b[mxn];
void cdq(int l,int r)
{
if(l==r) return;
int mid=(l+r)>>1;
cdq(l,mid); int lim = init(r-l+1);
for(int i=0;i<=mid-l;i++) a[i]=f[l+i];
for(int i=mid-l+1;i<=lim;i++) a[i]=0;
for(int i=0;i<=r-l;i++) b[i]=g[i];
for(int i=r-l+1;i<=lim;i++) b[i]=0;
NTT(a,lim,0); NTT(b,lim,0);
for(int i=0;i<lim;i++) a[i]=(ll)a[i]*b[i]%mdn;
NTT(a,lim,1);
//for(int i=0;i<lim;i++) printf("%d ",a[i]);
for(int i=mid+1;i<=r;i++) f[i]=(ll)(f[i]+a[i-l])%mdn;
cdq(mid+1,r);
}
int n;
int main()
{
scanf("%d",&n);
for(int i=1;i<n;i++) scanf("%d",&g[i]);
f[0]=1;
cdq(0,n);
for(int i=0;i<n;i++) printf("%d ",f[i]);
return 0;
}