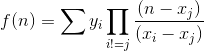CF622F The Sum of the k-th Powers
传送门
自然数幂和的拉格朗日插值求法
列出柿子
然后带一下值就可以了qwq
预处理分子分母啥的 见代码吧。
附代码。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define inf 20021225
#define ll long long
#define mdn 1000000007
#define mxk 1000010
using namespace std;
int n,k,tot,fm,fac[mxk],y,ans;
int ksm(int bs,int mi)
{
int ans=1;
while(mi)
{
if(mi&1) ans=(ll)ans*bs%mdn;
bs=(ll)bs*bs%mdn; mi>>=1;
}
return ans;
}
void solve(int x)
{
int s1=fac[x-1],s2=fac[k+2-x];
if((k+2-x)&1) s2=mdn-s2;
int tmp=(ll)tot*ksm(n-x,mdn-2)%mdn;
fm = (ll)s1*s2%mdn;
fm = (ll)ksm(fm,mdn-2)*tmp%mdn;
ans= (ans + (ll)y*fm%mdn)%mdn;
}
int main()
{
scanf("%d%d",&n,&k);
if(n<=k+2)
{
int ans=0;
for(int i=1;i<=n;i++) ans=(ans+ksm(i,k))%mdn;
printf("%d\n",ans);
return 0;
}
tot=fm=fac[0]=1;
for(int i=1;i<=k+2;i++) tot=(ll)tot*(n-i)%mdn,fac[i]=(ll)fac[i-1]*i%mdn;
for(int i=1;i<=k+2;i++) y=(y+ksm(i,k))%mdn,solve(i);
printf("%d\n",ans);
return 0;
}