2021年13届蓝桥杯B组C++省赛第一场题解
A 空间
主要考察计算机的基础知识计算机内部存储的换算如下
于是有
所以可装入256*1024*1024*8 / 32 = 67108864个
答案:
67108864
B 卡片
简单模拟
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N = 20;
int a[N];
int main()
{
for (int i = 0; i < 10; i ++) a[i] = 2021;
int flag = 0;
for (int i = 1; ; i ++) {
int k = i;
while (k) {
int x = k % 10;
if (!a[x]) flag = 1;
a[x] --;
k /= 10;
}
if (flag) { cout << i - 1; break; }
}
return 0;
}
答案:
3181
C 直线
问题描述

暴力低精度解法
考虑double的精度,本题最小的斜率为\(\frac{1} {20} = 0.05\)显然对于double来说精度足够。
根据直线方程\(y=kx+b\)可以通过两个点来求出对应的\(k\)和\(b\),只要加入到set去重即可。特别要注意的是,斜率和截距应该使用double本题数据量较小,所以不用考虑精度问题可能过
#include<bits/stdc++.h>
#define x first
#define y second
#define INF 0x3f3f3f3f
using namespace std;
typedef pair<double, double> PII;
set<PII> se;
int main ()
{
int n, m;
double t, c;
n = 20, m = 21;
for (int i = 0; i < n; i ++) {
for (int j = 0; j < m; j ++) {
PII a = {i, j};
for (int k = 0; k < n; k ++)
for (int l = 0; l < m; l ++) {
PII b = {k, l};
if (a.x == b.x && a.y == b.y) continue;
if (!(b.x-a.x)) { t = INF; c = a.x; se.insert({t, c}); }
else {
t = (b.y-a.y)*1.0 / (b.x-a.x)*1.0;
c = (b.x*a.y - a.x*b.y)*1.0 / (b.x-a.x)*1.0;
se.insert({t, c});
}
}
}
}
cout << se.size() << endl;
return 0;
}
答案:
40257
D货物摆放
问题描述

解答
先分析一下\(n\)含有多少个因子
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
vector<LL> vec;
int main()
{
LL n = 2021041820210418;
for (LL i = 1; i * i <= n; i ++) {
if (n % i == 0) {
vec.push_back(i);
LL k = n / i;
if (k != i) vec.push_back(k);
}
}
cout << vec.size();
return 0;
}
可以得出\(n\)仅有128个因子,所以直接枚举即可
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
vector<LL> vec;
int main()
{
LL n = 2021041820210418;
for (LL i = 1; i * i <= n; i ++) {
if (n % i == 0) {
vec.push_back(i);
LL k = n / i;
if (k != i) vec.push_back(k);
}
}
LL ans = 0;
for (auto a : vec)
for (auto b : vec)
for (auto c : vec)
if (a * b * c == n) ans ++;
cout << ans;
return 0;
}
答案:
2430
E 路径
问题描述

题解
欧几里得算法
解决这道题会用到最小公约数所以先来复习一下求最大公约数的欧几里德算法,欧几里得算法的核心其实是\(gcd(a, b) = gcd(b, a\ mod\ b)\)下面进行证明
-
对\(a\ mod \ b\)进行变换
\[\begin{align*} a\ mod\ b &= a - \left \lfloor \frac{a}{b} \right \rfloor \times b\\ &=a - c\times b \end{align*} \] -
证明对于\(a\)和\(b\)的任意公约数\(k\),都是\(b\)和\(a\ mod\ b\)的公约数
是\(b\)的公约数,同时也是\(a-c\times b\) 的公约数 -
证明对于\(b\)和\(a\ mod\ b\)的任意公约数\(m\),都是\(a\)和\(b\)的公约数
即证明\(m\)是\(a\)的公约数,\(m\)可以整除\(a\ mod\ b\),则\(m\)可以整除\(a-c\times b\)所以\(m\)可以整除\(a\)
综上所述,集合\(cd(a, b)\)等于集合\(cd(b, a\ mod\ b)\),则\(gcd(a, b) = gcd(b, a\ mod\ b)\),该过程的实现如下
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
根据题目描述用\(dijkstra\)算法求最短路即可。由于题中边数\(21\times 2021 = 42441\)点数为\(2021\)所以用朴素版的\(dijkstra\)算法即可时间复杂度为\(O(n^2)\)
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
using namespace std;
const int N = 3000;
int g[N][N], d[N];
bool st[N];
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
int dijkstra(int n) {
memset(d, INF, sizeof d);
d[1] = 0;
for (int i = 0; i < n; i ++) {
int k = INF, x;
for (int y = 1; y <= n; y ++) if (!st[y] && d[y] < k) k = d[x = y];
st[x] = true;
for (int y = 1; y <= n; y ++) d[y] = min(d[y], d[x] + g[x][y]);
}
if (d[n] == INF) return -1;
return d[n];
}
int main()
{
memset(g, INF, sizeof g);
for (int i = 1; i <= 2021; i ++)
for (int j = i + 1; j <= i + 21 && j <= 2021; j ++) {
g[i][j] = g[j][i] = i*j / gcd(i, j);
}
cout << dijkstra(2021);
return 0;
}
答案:
10266837
杨辉三角
暴力解法
由于题目中\(N\)的最大值为\(10^9\)暴力解法的时间复杂度为\(O(n^2)\)所以必然超时,结果只能过\(40\%\)
#include<bits/stdc++.h>
using namespace std;
const int N = 65000000;
int c[N];
int main ()
{
int ans = 0, t;
int flag = 0;
cin >> t;
for (int m = 1; m < N; m ++) {
c[0] = 1;
ans ++;
if (c[0] == t) break;
for (int i = 1; i <= m; i ++) {
ans ++;
c[i] = c[i-1] * (m-i+1) / i;
if (c[i] == t) { ans ++; flag = 1; break; }
}
if (flag) break;
}
cout << ans << endl;
return 0;
}
AC解法
组合数求法
LL C(int a, int b) {
int res = 1;
for (int i = a, j = 1; j <= b; j ++, i--) {
res = res * i / j;
if (res > n) return res; // 防止数值过大
}
return res;
}
分析
以中间为分割线,由于是从上至下从左至右进行计数,又由于杨辉三角是左右对称的所以第一次出现\(N\)只有可能是在左侧所以我们只考虑左侧的数。进一步通过观察发现,杨辉三角的每一行是递增的如果斜着观察如下图所示。
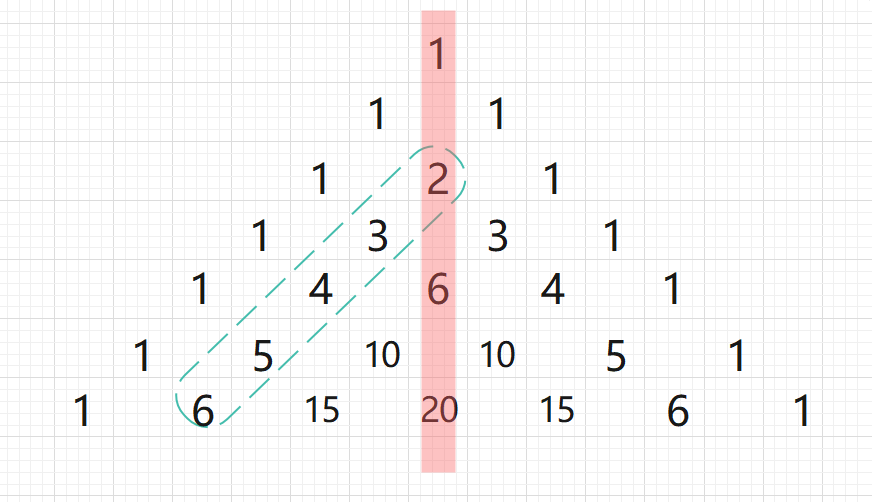
结果是递增的。右下角的数值应该是最大值,所以我们从内向外斜着枚举。观察到\(C^{17}_{34} > 10^9\)而\(C^{16}_{32}<10^9\)所以只需要从第16层斜着枚举即可,最后时间复杂度为\(16\times O(logN)\)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n;
LL C(int a, int b) {
LL res = 1;
for (int i = a, j = 1; j <= b; j ++, i --) {
res = res * i / j;
if (res > n) return res;
}
return res;
}
int main()
{
cin >> n;
for (int k = 16; ; k --) {
LL l = 2 * k, r = n;
while (l < r) {
int mid = l + r >> 1;
if (C(mid, k) >= n) r = mid;
else l = mid + 1;
}
if (C(l, k) == n) { cout << (1 + l) * l / 2 + k + 1 << endl; break; }
}
return 0;
}
砝码称重
暴力解法
直接爆搜枚举出所有的可能,当然只能过掉\(40\%\)的数据。
#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int w[N], n, ans;
set<int> st;
void dfs(int u, int weight) {
if (u == n) {
st.insert(weight);
return;
}
dfs(u + 1, abs(weight - w[u])); // 右边放w[u]的砝码
dfs(u + 1, weight); // 不放左右两边都不放
dfs(u + 1, abs(weight + w[u])); // 左边放w[u]的砝码
}
int main()
{
cin >> n;
for (int i = 0; i < n; i ++) scanf("%d", &w[i]);
dfs(0, 0);
cout << st.size() - 1 << endl;
return 0;
}


