后验概率最大化推导

李航统计学习方法第四章61页，后验概率最大化推到不太懂，参考了一些文章，懂了一丢丢（参考其他大佬的博客的，大部分都是大佬写的哈哈哈哈，我是搬运工，原文链接以放出）

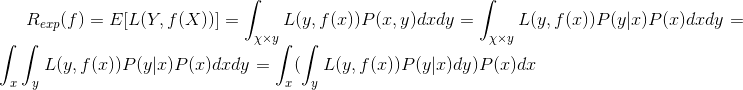
在这里，设:

 

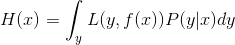
那么上式可以改为:

 

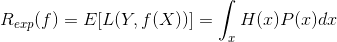
对于上式的期望风险求最小化，可以发现这是一个积分，积分中的中的各项以及都大于0，所以积分过程中不存在积分域内的两块积分相减的情况，因此求最小值就是求的最小值。对于任意的一个，为常数，那么最小值一定是在取最小值的时候取到。因此对期望风险函数的求解可以转为所谓的求条件期望的最小值：

 

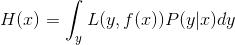
对于离散型随机变量，可以变换为：（这里不太懂是什么意思）

 

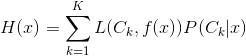
在书中还有一句就是对逐个极小化，还是由于和都是大于0的，那么要求的最小化就要使其中的每一项取最小值。

随后的化简过程就比较简单了，这里不再赘述

原文链接：https://blog.csdn.net/yaokun2012/article/details/81913129