java排序算法（三）：堆排序

java排序算法（三）堆排序

堆积排序（HeapSort）是指利用堆积树这种结构所设计的排序算法，可以利用数组的特点快速定位指定索引的元素。堆排序是不稳定的排序方法。辅助空间为O(1).最坏时间复杂度为O(nlog2n)

堆排序的堆序的平均性能较接近于最坏性能

堆排序利用大根堆（或者小根堆）堆顶记录的关键字最大（或者最小）这一特征。使得在当前无序区中选中最大（或者最小）关键字的记录变的简单

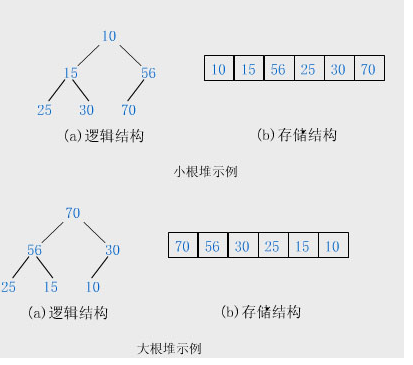
（1）最大堆的排序思想

·　　1、先将初始文件R[1..n]建成一个大根堆，此堆为初始的无序区

　　 2、再将关键字最大的记录R[1]即堆顶和无序区的最后一个记录R[n]交换。由此得到新的无序区R[1..n-1]和有序区R[n].且满足R[1..n-1].keys <=R[n].key

　　3、由于交换后新的根R[1]可能违反堆性质，故应将当前无序区R[1..n-1]调整为堆，然后再次将R[1..n-1]和该区的最后一个记录R[n+1]交换。由此得到新的无序区R[1,n-2]和有序区

　　　R[1,n-2].keys<=R[n,n-1].keys,同样将R[1..n-2]调整为堆

　　直接无序区只有一个元素为止

（2）大根堆排序的基本操作

　　1、初始化操作；将R[1.n]构造为初始堆

　　2、每一趟排序的基本操作，将当前无序区的堆顶记录R[1]和该区间的最后一个记录交换。然后将新的无序区调整为堆

　　注意：

　　1、只需做n-1趟排序，选出较大的n-1个关键字即可以使得文件递增有序

　　2、小根堆排序和大根堆排序类似。只不过排序结果是递减有序的。堆排序和直接选择排序相反。在任何时刻堆排序中无序区总是在有序区之前。且有序区是在原向量的尾部右后往前逐步扩大到整个向量为止。

代码实现

package com.spring.test;

import java.util.zip.DataFormatException;

/**
 * 堆排序
 */
public class HeapSortTest {
    public static void main(String[] args) {
        int[] data5 = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };
        print(data5);
        heapSort(data5);
        System.out.println("排序后的数组");
        print(data5);

    }

    public static void heapSort(int[] data){
        for(int i=0;i<data.length;i++){
            createMaxdHeap(data,data.length-1-i);
            swap(data,0,data.length-1-i);
            print(data);
        }
    }


    /**
     * 交换数据
     */
    public static void swap(int[] data,int i,int j){
        if(i==j){
            return;
        }
        data[i] = data[i]+data[j];
        data[j] = data[i]-data[j];
        data[i] = data[i]-data[j];
    }

    /**
     * 打印输出
     */
    public static void print(int[] data){
        for(int i=0;i<data.length;i++){
            System.out.print(data[i]+"\t");
        }
        System.out.println();
    }

    /**
     * 大根堆进行判断
     */
    public static void createMaxdHeap(int[] data,int lastIndex){
        for(int i =(lastIndex-1)/2;i >=0;i--){
            //保存当前正在判断的节点
            int k = i;
            //若当前节点的子节点存在
            while(2*k+1 <= lastIndex){
                //biggerIndex总是记录较大节点的值，先赋值当前判断节点的左子节点
                int biggerIndex = 2*k +1;
                if(biggerIndex < lastIndex){
                    //若右子节点存在，否则此时biggerIndex应该等于lastIndex
                    if(data[biggerIndex] < data[biggerIndex + 1]){
                        //若右子节点值比左子节点值大，则biggerIndex记录的是右子节点的值
                        biggerIndex++;
                    }
                }
                if(data[k] < data[biggerIndex]){
                    /**
                     * 若当前节点的值比子节点的最大值小，则交换两者的值，，交换后将biggerIndex赋值给K
                     *
                     */
                    swap(data,k,biggerIndex);
                    k = biggerIndex;
                }else{
                    break;
                }
            }
        }
    }

}

排序结果