堆排序，C++模板编程

明天就要去参加百度的笔试了，现在来抱抱佛教。

 

理论来自：简明现代魔法

在程序设计相关领域，堆(Heap)的概念主要涉及到两个方面：

• 一种数据结构，逻辑上是一颗完全二叉树，存储上是一个数组对象（二叉堆）。
• 垃圾收集存储区，是软件系统可以编程的内存区域。

本文所说的堆，指的是前者。

堆排序的时间复杂度是O(nlgN)，与快速排序达到相同的时间复杂度。但是在实际应用中，我们往往采用快速排序而不是堆排序。这是因为快速排序的一个好的实现，往往比堆排序具有更好的表现。堆排序的主要用途，是在形成和处理优先级队列方面。另外，如果计算要求是类优先级队列（比如，只要返回最大或者最小元素，只有有限的插入要求等），堆同样是很适合的数据结构。

基础知识

堆一般用数组表示，比如数组A数组的长度Length(A)，堆在数组中的元素个数HeapSize(A)。一般说来，HeapSize(A) <= Length(A)，因为数组A当中可能有一些元素不在堆中。

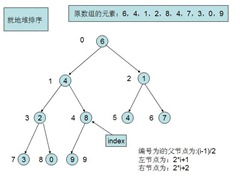
假设节点I是数组A中下标为i的节点。

• Parent(i) : return Floor(i/2); //I的父节点下标，Floor(i)表示比i小的最大整数。
• Left(i) : return 2*i; //I的左子节点
• Right(i) : return 2*i+1; //I的右子节点

含有n个元素的堆A的高度是: Floor(lgn)。

堆的基本操作

• MaxHeapify( A, i ):

  保持堆的性质。假设数组A和下标i，假定以Left(i)和Right(i)为根结点的左右两棵子树都已经是最大堆，节点i的值可能小于其子节点。调整节点i的位置。

• BuildMaxHeap( A ):

  从一个给定的数组建立最大堆。子数组A[ floor(n/2)+1 .... ... n]中的元素都是树的叶节点(完全二叉树的基本性质)。从索引 ceiling(n/2)开始一直到1，对每一个元素都执行MaxHeapify，最终得到一个最大堆。

• 堆排序 HeapSort( A ):

  堆排序算法的基本思想是，将数组A创建为一个最大堆，然后交换堆的根(最大元素)和最后一个叶节点x，将x从堆中去掉形成新的堆A1，然后重复以上动作，直到堆中只有一个节点。

• 优先级队列算法-增加某元素的值(优先级) : HeapIncreaseKey( A, i, key )

  增加某一个元素的优先级后（元素的值），该元素应该向上移动，才能保持堆的性质。

• 优先级队列算法-插入一个元素: Insert( S, x ) 将x元素插入到优先级队列S中。

  主要思路是，将堆的最后一个叶节点之后，扩展一个为无穷小的新叶节点，然后增大它的值为x的值。

 

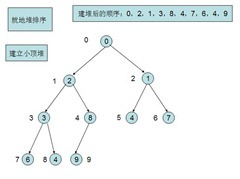
本来我只打算随便写个小程序的，但是发现，可以写个更通用的程序。以最小堆为例，说下建堆和排序的过程。

经过上面两个步骤，就成功的建立了一个最小堆。排序的过程就是取出堆顶元素push到临时数组，然后将堆顶元素和最后一个元素交换，再pop掉最后一个元素，直到堆中没有元素。这样就获得了一个有序的数组，然后在复制到堆中。

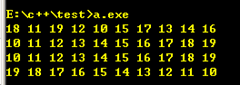
完整程序如下：

//最小堆排序和最大堆排序

#include <algorithm>
#include <functional>
#include <vector>
#include <iostream>
using namespace std;

template<typename Type>
class Heap
{
public:
    Heap(const vector<Type>& a_array)
    {
        m_array.assign(a_array.begin(),a_array.end());
    }

    template<typename Compare>
    void sort(Compare comp);

    void printArray(const vector<Type>& a_array);

private:
    vector<Type> m_array;

    //comp 为less<Type> 则大数下沉，创建最小堆，从小到大排序
    //comp 为greater<Type> 则小数下沉，创建最大堆，从大到小排序
    template<typename Compare>
    void creatHeap(Compare comp);                //创建堆

    template<typename Compare>
    void downElement(int a_elem, Compare comp);    //下沉元素
};

template<typename Type>
template<typename Compare>
void Heap<Type>::sort(Compare comp)
{
    printArray(m_array);
    creatHeap(comp);                    //建堆
    vector<Type> array;
    for (int i = m_array.size() - 1; i >= 0; i--)
    {
        array.push_back(m_array[0]);    //保留堆顶
        swap(m_array[0], m_array[i]);    //交换
        m_array.pop_back();                //去掉最后一个元素
        downElement(0,comp);            //将新的首元素下沉
    }
    printArray(array);
    m_array.assign(array.begin(),array.end());
}

template<typename Type>
template<typename Compare>
void Heap<Type>::creatHeap(Compare comp)
{
    //从最后一个非叶子节点开始，将每个父节点都调整为最小堆
    for (int i=m_array.size()/2-1; i>=0; i--)
    {
        downElement(i, comp);
    }
}

template<typename Type>
template<typename Compare>
void Heap<Type>::downElement(int a_elem, Compare comp)    //下沉元素
{
    int min;            //设置最小元素下标
    int index = a_elem;    //当前下沉的元素下标
    while (index*2+1 < m_array.size())//存在左节点
    {
        min = index*2+1;
        if (index*2+2 < m_array.size())//存在右节点
        {
            //左右节点比较，选出最小的
            if (comp(m_array[index*2+2],m_array[min]))
            {
                min = index*2+2;
            }
        }
        //同子节点比较，若父节点最小则结束
        if (comp(m_array[index],m_array[min]))
        {
            break;
        }
        else//选最小元素到父节点
        {
            swap(m_array[min],m_array[index]);
            index = min;
        }
    }
}

template<typename Type>
void Heap<Type>::printArray(const vector<Type>& a_array)
{
    for (int i=0; i<a_array.size(); i++)
    {
        cout << a_array[i] << " ";
    }
    cout << endl;
}


int main()
{
    vector<int> array;
    for (int i=10; i<20; i++)
    {
        array.push_back(i);
    }
    random_shuffle(array.begin(), array.end());//打乱顺序
    Heap<int> heap(array);
    heap.sort(less<int>());
    heap.sort(greater<int>());
    return 0;
}