CF1039D You Are Given a Tree
You Are Given a Tree
题面翻译
有一棵 \(n\) 个节点的树。
其中一个简单路径的集合被称为 \(k\) 合法当且仅当：
树的每个节点至多属于其中一条路径，且每条路径恰好包含 \(k\) 个点。
对于 \(k\in [1,n]\)，求出 \(k\) 合法路径集合的最多路径数
即：设 \(k\) 合法路径集合为 \(S\)，求最大的 \(|S|\)。
\(n \leq 10^5\)。
题目描述
A tree is an undirected graph with exactly one simple path between each pair of vertices. We call a set of simple paths $ k $ -valid if each vertex of the tree belongs to no more than one of these paths (including endpoints) and each path consists of exactly $ k $ vertices.
You are given a tree with $ n $ vertices. For each $ k $ from $ 1 $ to $ n $ inclusive find what is the maximum possible size of a $ k $ -valid set of simple paths.
输入格式
The first line of the input contains a single integer $ n $ ( $ 2 \le n \le 100,000 $ ) — the number of vertices in the tree.
Then following $ n - 1 $ lines describe the tree, each of them contains two integers $ v $ , $ u $ ( $ 1 \le v, u \le n $ ) — endpoints of the corresponding edge.
It is guaranteed, that the given graph is a tree.
输出格式
Output $ n $ numbers, the $ i $ -th of which is the maximum possible number of paths in an $ i $ -valid set of paths.
样例 #1
样例输入 #1
7
1 2
2 3
3 4
4 5
5 6
6 7
样例输出 #1
7
3
2
1
1
1
1
样例 #2
样例输入 #2
6
1 2
2 3
2 4
1 5
5 6
样例输出 #2
6
2
2
1
1
0
提示
One way to achieve the optimal number of paths for the second sample is illustrated in the following picture:
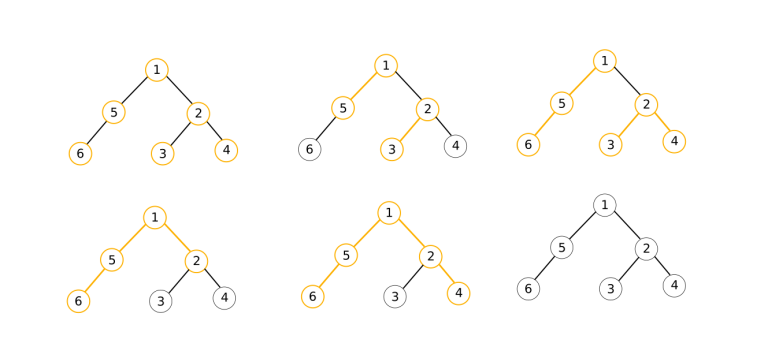
Solution
学习根号分治的好题。
首先可以知道的是，确定 \(k\) 过后，答案最多是 \(\dfrac{n}{k}\)，根据整除分块的思想可以得知这个答案的值只会有 \(\mathcal O(\sqrt n)\) 种取值方法。并且随着 \(k\) 的增大答案在不停减小。
根据这些，可以得知最后的结果应该是类似于整除分块一样的形式，递减并且相等的答案一定是连续的。
会发现，这个答案序列的前半部分的变化幅度很大，后半部分的变化幅度很小，因此可以设置一个阈值 \(siz\)，小于等于 \(siz\) 的部分暴力做，大于的部分暴力做完二分找到答案连续段的右端点。这道题就完成了大半了。
考虑已知 \(k\) 如何计算答案。可以从下往上贪心，如果当前链的长度已经大于等于了 \(k\)，那么就将答案加一。具体写法可以参考代码进行理解。
// Problem: You Are Given a Tree
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF1039D
// Memory Limit: 500 MB
// Time Limit: 7000 ms
// Author: Hanx16QwQ
#include<bits/stdc++.h>
using namespace std;
namespace Hanx16qwq {
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
char buf[1 << 23], *p1 = buf, *p2 = buf;
template<class T> inline void read(T &x) {
x = 0; T flag = 1; char b = getchar();
while (!isdigit(b)) {flag = b == '-' ? -1 : 1; b = getchar();}
while (isdigit(b)) {x = x * 10 + b - 48; b = getchar();}
x *= flag;
}
template<class T, typename... Args> inline void read(T &x, Args&... args) {
read(x), read(args...);
}
template<class T> inline void write(T x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
template<class T> inline void writewith(T x, char c) {
write(x), putchar(c);
}
const int _SIZE = 1e5;
int n;
struct EDGE {
int nxt, to;
}edge[(_SIZE << 1) + 5];
int tot, head[_SIZE + 5];
void AddEdge(int x, int y) {
edge[++tot] = {head[x], y};
head[x] = tot;
}
int dfn[_SIZE + 5], fa[_SIZE + 5], cnt;
int order[_SIZE + 5];
void Dfs(int x, int F) {
dfn[x] = ++cnt, order[cnt] = x, fa[x] = F;
for (int i = head[x]; i; i = edge[i].nxt) {
int twd = edge[i].to;
if (twd == F) continue;
Dfs(twd, x);
}
}
int fm[_SIZE + 5], fs[_SIZE + 5];
int Solve(int k) {
memset(fm, 0, sizeof fm);
memset(fs, 0, sizeof fs);
int res = 0;
for (int i = n; i; --i) {
int x = order[i], y = fa[x];
if (fm[x] + fs[x] + 1 >= k) {
fm[x] = fs[x] = 0;
++res;
} else {
if (fm[y] < fm[x] + 1)
fs[y] = fm[y], fm[y] = fm[x] + 1;
else if (fs[y] < fm[x] + 1)
fs[y] = fm[x] + 1;
}
}
return res;
}
void main() {
read(n);
int siz = sqrt(n * __lg(n));
for (int i = 1, x, y; i < n; ++i) {
read(x, y);
AddEdge(x, y), AddEdge(y, x);
}
Dfs(1, 0);
for (int k = 1; k <= n; ++k) {
if (k <= siz) writewith(Solve(k), '\n');
else {
int ans = Solve(k);
int l = k, r = n;
while (l <= r) {
int mid = (l + r) >> 1;
if (Solve(mid) != ans) r = mid - 1;
else l = mid + 1;
}
for (int i = k; i <= r; ++i)
writewith(ans, '\n');
k = r;
}
}
}
}
signed main() {
Hanx16qwq::main();
return 0;
}
