P4001 [ICPC-Beijing 2006] 狼抓兔子
[ICPC-Beijing 2006] 狼抓兔子
题目描述
现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的,而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个网格的地形:
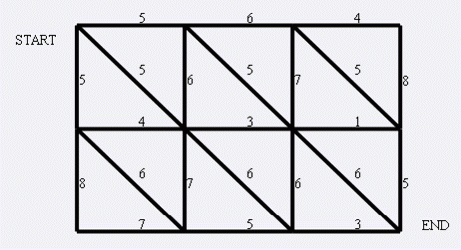
左上角点为 \((1,1)\), 右下角点为 \((N,M)\) (上图中 \(N=3\), \(M=4\)).有以下三种类型的道路:
-
\((x,y)\rightleftharpoons(x+1,y)\)
-
\((x,y)\rightleftharpoons(x,y+1)\)
-
\((x,y)\rightleftharpoons(x+1,y+1)\)
道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的。左上角和右下角为兔子的两个窝,开始时所有的兔子都聚集在左上角 \((1,1)\) 的窝里,现在它们要跑到右下角 \((N,M)\) 的窝中去,狼王开始伏击这些兔子。当然为了保险起见,如果一条道路上最多通过的兔子数为 \(K\),狼王需要安排同样数量的 \(K\) 只狼,才能完全封锁这条道路,你需要帮助狼王安排一个伏击方案,使得在将兔子一网打尽的前提下,参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。
输入格式
第一行两个整数 \(N,M\),表示网格的大小。
接下来分三部分。
第一部分共 \(N\) 行,每行 \(M-1\) 个数,表示横向道路的权值。
第二部分共 \(N-1\) 行,每行 \(M\) 个数,表示纵向道路的权值。
第三部分共 \(N-1\) 行,每行 \(M-1\) 个数,表示斜向道路的权值。
输出格式
输出一个整数,表示参与伏击的狼的最小数量。
样例 #1
样例输入 #1
3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
样例输出 #1
14
提示
数据规模与约定
对于全部的测试点,保证 \(3 \leq N,M \leq 1000\),所有道路的权值均为不超过 \(10^6\) 的正整数。
Solution
第一眼看到这道题,想这不是最小割模板?然后就直接打了一个 dinic 求最小割交上去直接 AC 了。看了一眼讨论区,才发现是因为 dinic 的玄学优化,导致 1e6 的数据完完全全跑不满,所以可以 AC 这道题。实际上这样的数据规模是预流推进都跑不过去的。
那该怎么做这道题呢?这时候就要引入一个东西了:对偶图。
对偶图是将平面图的连通性信息转换为一张图存储的东西。
比如原图长这个样子:

那么它的对偶图就长这个样子:

对偶图上每条边的边权就等于它穿过的原图上的边的边权。
可以发现,对偶图上一条从源点到汇点的路径刚好可以将原图切割成为两半。也就是说,对偶图上 \(S\rightarrow T\) 的最短路就是原图的最小割。
所以建出对偶图过后直接用 DIJ 跑个最短路就行了。
至于建图,自己画一画,想一想怎么建就行了,具体建图方式也不好说。
#include<bits/stdc++.h>
using namespace std;
namespace Hanx16qwq {
constexpr int _SIZE = 2e6;
int n, m, temp;
struct EDGE{
int nxt, to, l;
}edge[(_SIZE << 4) + 5];
int tot, head[_SIZE + 5];
void AddEdge(int x, int y, int l) {
edge[++tot] = {head[x], y, l}; head[x] = tot;
edge[++tot] = {head[y], x, l}; head[y] = tot;
}
int Num(int x, int y) {
return (x - 1) * (m - 1) + y;
}
int S, T;
int dist[_SIZE + 5];
bool vis[_SIZE + 5];
void DIJ() {
priority_queue<pair<int, int>> q;
q.emplace(0, S);
memset(dist, 0x3f, sizeof dist); dist[S] = 0;
while (!q.empty()) {
int cur = q.top().second; q.pop();
if (vis[cur]) continue; vis[cur] = 1;
if (cur == T) return;
for (int i = head[cur]; i; i = edge[i].nxt) {
int twd = edge[i].to;
if (dist[twd] > dist[cur] + edge[i].l) {
dist[twd] = dist[cur] + edge[i].l;
q.emplace(-dist[twd], twd);
}
}
}
}
void main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> m; S = 2e6 + 1, T = 2e6 + 2;
for (int i = 1; i <= n; i++)
for (int j = 1; j < m; j++) {
cin >> temp;
if (i == 1) AddEdge(Num(1, j), T, temp);
else if (i == n) AddEdge(S, Num((i - 1) * 2, j), temp);
else AddEdge(Num((i - 1) * 2, j), Num(i * 2 - 1, j), temp);
}
for (int i = 1; i < n; i++)
for (int j = 1; j <= m; j++) {
cin >> temp;
if (j == 1) AddEdge(S, Num(i * 2, j), temp);
else if (j == m) AddEdge(Num(i * 2 - 1, j - 1), T, temp);
else AddEdge(Num(i * 2 - 1, j - 1), Num(i * 2, j), temp);
}
for (int i = 1; i < n; i++)
for (int j = 1; j < m; j++) {
cin >> temp;
AddEdge(Num(i * 2, j), Num(i * 2 - 1, j), temp);
}
DIJ();
cout << dist[T] << '\n';
}
}
signed main() {
Hanx16qwq::main();
return 0;
}


