CSP-S 2022 T1~T3 题解

T1 假期计划

题目描述

小熊的地图上有 \(n\) 个点，其中编号为 \(1\) 的是它的家、编号为 \(2, 3, \ldots, n\) 的都是景点。部分点对之间有双向直达的公交线路。如果点 \(x\) 与 \(z_1\)、\(z_1\) 与 \(z_2\)、……、\(z_{k - 1}\) 与 \(z_k\)、\(z_k\) 与 \(y\) 之间均有直达的线路，那么我们称 \(x\) 与 \(y\) 之间的行程可转车 \(k\) 次通达；特别地，如果点 \(x\) 与 \(y\) 之间有直达的线路，则称可转车 \(0\) 次通达。

很快就要放假了，小熊计划从家出发去 \(4\) 个不同的景点游玩，完成 \(5\) 段行程后回家：家 \(\to\) 景点 A \(\to\) 景点 B \(\to\) 景点 C \(\to\) 景点 D \(\to\) 家且每段行程最多转车 \(k\) 次。转车时经过的点没有任何限制，既可以是家、也可以是景点，还可以重复经过相同的点。例如，在景点 A \(\to\) 景点 B 的这段行程中，转车时经过的点可以是家、也可以是景点 C，还可以是景点 D \(\to\) 家这段行程转车时经过的点。

假设每个景点都有一个分数，请帮小熊规划一个行程，使得小熊访问的四个不同景点的分数之和最大。

输入格式

第一行包含三个正整数 \(n, m, k\)，分别表示地图上点的个数、双向直达的点对数量、每段行程最多的转车次数。

第二行包含 \(n - 1\) 个正整数，分别表示编号为 \(2, 3, \ldots, n\) 的景点的分数。

接下来 \(m\) 行，每行包含两个正整数 \(x, y\)，表示点 \(x\) 和 \(y\) 之间有道路直接相连，保证 \(1 \le x, y \le n\)，且没有重边，自环。

输出格式

输出一个正整数，表示小熊经过的 \(4\) 个不同景点的分数之和的最大值。

样例 #1

样例输入 #1

8 8 1
9 7 1 8 2 3 6
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 1

样例输出 #1

样例 #2

样例输入 #2

7 9 0
1 1 1 2 3 4
1 2
2 3
3 4
1 5
1 6
1 7
5 4
6 4
7 4

样例输出 #2

提示

【样例解释 #1】

当计划的行程为 \(1 \to 2 \to 3 \to 5 \to 7 \to 1\) 时，\(4\) 个景点的分数之和为 \(9 + 7 + 8 + 3 = 27\)，可以证明其为最大值。

行程 \(1 \to 3 \to 5 \to 7 \to 8 \to 1\) 的景点分数之和为 \(24\)、行程 \(1 \to 3 \to 2 \to 8 \to 7 \to 1\) 的景点分数之和为 \(25\)。它们都符合要求，但分数之和不是最大的。

行程 \(1 \to 2 \to 3 \to 5 \to 8 \to 1\) 的景点分数之和为 \(30\)，但其中 \(5 \to 8\) 至少需要转车 \(2\) 次，因此不符合最多转车 \(k = 1\) 次的要求。

行程 \(1 \to 2 \to 3 \to 2 \to 3 \to 1\) 的景点分数之和为 \(32\)，但游玩的并非 \(4\) 个不同的景点，因此也不符合要求。

【样例 #3】

见附件中的 holiday/holiday3.in 与 holiday/holiday3.ans。

【数据范围】

对于所有数据，保证 \(5 \le n \le 2500\)，\(1 \le m \le 10000\)，\(0 \le k \le 100\)，所有景点的分数 \(1 \le s_i \le {10}^{18}\)。保证至少存在一组符合要求的行程。

测试点编号	\(n \le\)	\(m \le\)	\(k \le\)
\(1 \sim 3\)	\(10\)	\(20\)	\(0\)
\(4 \sim 5\)	\(10\)	\(20\)	\(5\)
\(6 \sim 8\)	\(20\)	\(50\)	\(100\)
\(9 \sim 11\)	\(300\)	\(1000\)	\(0\)
\(12 \sim 14\)	\(300\)	\(1000\)	\(100\)
\(15 \sim 17\)	\(2500\)	\(10000\)	\(0\)
\(18 \sim 20\)	\(2500\)	\(10000\)	\(100\)

Solution

感觉 T1 甚至比 T2 还难。

看到数据范围，直接尝试开 \(\mathcal O(n^2)\) 的做法。

先预处理出来每个点在 \(k\) 步之内可以到达哪些点，存储在一个 vector 内，这一步时间复杂度是 \(\mathcal O(n(n+m))\) 的。然后注意到路径可以拆成相同的两半，也就是只计算从起点出发走两个点的最大值，预处理出这个值存在 f[][] 内，然后枚举 \(B,C\) 点，取最大的 \(A,D\) 点即可，注意到可能出现冲突的情况，所以在草稿本上画一下可以知道是取前三大即可。

考场思路是这样的，结果洛谷上挂了一个点，原因是没有判断连通性。解决办法也很简单，就是将 f 的初值赋值为一个极小值，这样就不会对答案产生贡献了。

赛时 95 分。

#include<bits/stdc++.h>
using namespace std;
constexpr int _SIZE = 2.5e3, _ESIZE = 1e4;
struct EDGE{
	int nxt, to;
}edge[(_ESIZE << 1) + 5];
int tot, head[_SIZE + 5];
void AddEdge(int x, int y) {
	edge[++tot] = {head[x], y};
	head[x] = tot;
}
int n, k, m;
long long val[_SIZE + 5], ans = 0xcfcfcfcfcfcfcfcf;
long long f[_SIZE + 5][_SIZE + 5];
int from[_SIZE + 5][_SIZE + 5], cnt[_SIZE + 5];
bool vis[_SIZE + 5];
pair<int, int> q[(_SIZE << 1) + 5];
void bfs(int s) {
	int hed = 1, tal = 1;
	memset(vis, 0, sizeof vis);
	vis[s] = 1;
	q[++tal] = make_pair(s, -1);
	while (hed <= tal) {
		int x = q[hed].first, step = q[hed].second; hed++;
		if (step == k) continue;
		for (int i = head[x]; i; i = edge[i].nxt) {
			int twd = edge[i].to;
			if (vis[twd]) continue;
			vis[twd] = 1;
			q[++tal] = make_pair(twd, step + 1);
			from[s][++cnt[s]] = twd;
		}
	}
}
int maxn[_SIZE + 5][5];
vector<int> sec;
unordered_map<int, bool> H;
void init() {
	memset(f, 0xcf, sizeof f);
	for (int i = 1; i <= cnt[1]; i++) {
		int A = from[1][i];
		for (int j = 1; j <= cnt[A]; j++) {
			int B = from[A][j];
			f[A][B] = val[A] + val[B];
			if (H.find(B) == H.end()) sec.push_back(B), H[B] = 1;
			if (f[A][B] > f[maxn[B][1]][B]) 
				maxn[B][3] = maxn[B][2], maxn[B][2] = maxn[B][1], maxn[B][1] = A;
			else if (f[A][B] > f[maxn[B][2]][B])
				maxn[B][3] = maxn[B][2], maxn[B][2] = A;
			else if (f[A][B] > f[maxn[B][3]][B])
				maxn[B][3] = A;
		}
	}
}
bool check(int T1, int T2, int T3, int T4) {
	return !(T1 == T2 || T2 == T3 || T3 == T4 || T1 == T4 || T2 == T4 || T1 == T3);
}
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> m >> k;
	for (int i = 2; i <= n; i++) cin >> val[i];
	for (int i = 1; i <= m; i++) {
		static int u, v;
		cin >> u >> v;
		AddEdge(u, v), AddEdge(v, u);
	}
	for (int i = 1; i <= n; i++) bfs(i);
	init();
	for (auto B: sec) {
		for (int i = 1; i <= cnt[B]; i++) {
			int C = from[B][i];
			long long fmaxn1 = f[maxn[B][1]][B], fmaxn2 = f[maxn[B][2]][B], fmaxn3 = f[maxn[B][3]][B];
			long long lmaxn1 = f[maxn[C][1]][C], lmaxn2 = f[maxn[C][2]][C], lmaxn3 = f[maxn[C][3]][C];
			if (check(maxn[B][1], B, maxn[C][1], C)) ans = max(fmaxn1 + lmaxn1, ans);
			if (check(maxn[B][1], B, maxn[C][2], C)) ans = max(fmaxn1 + lmaxn2, ans);
			if (check(maxn[B][1], B, maxn[C][3], C)) ans = max(fmaxn1 + lmaxn3, ans);
			if (check(maxn[B][2], B, maxn[C][1], C)) ans = max(fmaxn2 + lmaxn1, ans);
			if (check(maxn[B][2], B, maxn[C][2], C)) ans = max(fmaxn2 + lmaxn2, ans);
			if (check(maxn[B][2], B, maxn[C][3], C)) ans = max(fmaxn2 + lmaxn3, ans);
			if (check(maxn[B][3], B, maxn[C][1], C)) ans = max(fmaxn3 + lmaxn1, ans);
			if (check(maxn[B][3], B, maxn[C][2], C)) ans = max(fmaxn3 + lmaxn2, ans);
			if (check(maxn[B][3], B, maxn[C][3], C)) ans = max(fmaxn3 + lmaxn3, ans);
		}
	}
	cout << ans << '\n';
	return 0;
}

T2 策略游戏

题目描述

小 L 和小 Q 在玩一个策略游戏。

有一个长度为 \(n\) 的数组 \(A\) 和一个长度为 \(m\) 的数组 \(B\)，在此基础上定义一个大小为 \(n \times m\) 的矩阵 \(C\)，满足 \(C_{i j} = A_i \times B_j\)。所有下标均从 \(1\) 开始。

游戏一共会进行 \(q\) 轮，在每一轮游戏中，会事先给出 \(4\) 个参数 \(l_1, r_1, l_2, r_2\)，满足 \(1 \le l_1 \le r_1 \le n\)、\(1 \le l_2 \le r_2 \le m\)。

游戏中，小 L 先选择一个 \(l_1 \sim r_1\) 之间的下标 \(x\)，然后小 Q 选择一个 \(l_2 \sim r_2\) 之间的下标 \(y\)。定义这一轮游戏中二人的得分是 \(C_{x y}\)。

小 L 的目标是使得这个得分尽可能大，小 Q 的目标是使得这个得分尽可能小。同时两人都是足够聪明的玩家，每次都会采用最优的策略。

请问：按照二人的最优策略，每轮游戏的得分分别是多少？

输入格式

第一行输入三个正整数 \(n, m, q\)，分别表示数组 \(A\)，数组 \(B\) 的长度和游戏轮数。

第二行：\(n\) 个整数，表示 \(A_i\)，分别表示数组 \(A\) 的元素。

第三行：\(m\) 个整数，表示 \(B_i\)，分别表示数组 \(B\) 的元素。

接下来 \(q\) 行，每行四个正整数，表示这一次游戏的 \(l_1, r_1, l_2, r_2\)。

输出格式

输出共 \(q\) 行，每行一个整数，分别表示每一轮游戏中，小 L 和小 Q 在最优策略下的得分。

样例 #1

样例输入 #1

样例输出 #1

0
4

样例 #2

样例输入 #2

6 4 5
3 -1 -2 1 2 0
1 2 -1 -3
1 6 1 4
1 5 1 4
1 4 1 2
2 6 3 4
2 5 2 3

样例输出 #2

提示

【样例解释 #1】

这组数据中，矩阵 \(C\) 如下：

\[\begin{bmatrix} 0 & 0 \\ -3 & 4 \\ 6 & -8 \end{bmatrix} \]

在第一轮游戏中，无论小 L 选取的是 \(x = 2\) 还是 \(x = 3\)，小 Q 都有办法选择某个 \(y\) 使得最终的得分为负数。因此小 L 选择 \(x = 1\) 是最优的，因为这样得分一定为 \(0\)。

而在第二轮游戏中，由于小 L 可以选 \(x = 2\)，小 Q 只能选 \(y = 2\)，如此得分为 \(4\)。

【样例 #3】

见附件中的 game/game3.in 与 game/game3.ans。

【样例 #4】

见附件中的 game/game4.in 与 game/game4.ans。

【数据范围】

对于所有数据，\(1 \le n, m, q \le {10}^5\)，\(-{10}^9 \le A_i, B_i \le {10}^9\)。对于每轮游戏而言，\(1 \le l_1 \le r_1 \le n\)，\(1 \le l_2 \le r_2 \le m\)。

测试点编号	\(n, m, q \le\)	特殊条件
\(1\)	\(200\)	1, 2
\(2\)	\(200\)	1
\(3\)	\(200\)	2
\(4 \sim 5\)	\(200\)	无
\(6\)	\(1000\)	1, 2
\(7 \sim 8\)	\(1000\)	1
\(9 \sim 10\)	\(1000\)	2
\(11 \sim 12\)	\(1000\)	无
\(13\)	\({10}^5\)	1, 2
\(14 \sim 15\)	\({10}^5\)	1
\(16 \sim 17\)	\({10}^5\)	2
\(18 \sim 20\)	\({10}^5\)	无

其中，特殊性质 1 为：保证 \(A_i, B_i > 0\)。
特殊性质 2 为：保证对于每轮游戏而言，要么 \(l_1 = r_1\)，要么 \(l_2 = r_2\)。

Solution

第一眼以为要博弈论了，结果发现就是个简单题。

很容易会发现答案肯定与区间最大最小值有关，所以直接先对两个序列维护 \(4\) 个 ST 表。对答案分类讨论，按照两个区间内包含元素的值域进行讨论，每个分为 \([-,+]\)，\([-,-]\)，\([+,+]\) 的情况，总共 \(9\) 类讨论就行了，发现当二者都是 \([-,+]\) 的时候答案不一定与最大最小值相关，所以再维护一个非负数的最小值和非正数的最大值即可。考场实测，推出这些结论不到 \(5\) 分钟。

赛时 AC。

#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int _SIZE = 1e5;
int n, m, q;
int a[_SIZE + 5], b[_SIZE + 5];
int amax[_SIZE + 5][25], amin[_SIZE + 5][25], aex1[_SIZE + 5][25], aex2[_SIZE + 5][25];
int bmax[_SIZE + 5][25], bmin[_SIZE + 5][25];
void init() {
	for (int i = 1; i <= n; i++) {
		amax[i][0] = amin[i][0] = a[i];
		if (a[i] > 0) aex1[i][0] = a[i], aex2[i][0] = INT_MIN;
		else if (a[i] < 0) aex1[i][0] = INT_MAX, aex2[i][0] = a[i];
		else aex1[i][0] = aex2[i][0] = 0;
	}
	for (int i = 1; i <= m; i++) bmax[i][0] = bmin[i][0] = b[i];
	for (int i = 1; i <= 20; i++)
		for (int j = 1; j + (1 << i) - 1 <= n; j++) {
			amax[j][i] = max(amax[j][i - 1], amax[j + (1 << (i - 1))][i - 1]);
			amin[j][i] = min(amin[j][i - 1], amin[j + (1 << (i - 1))][i - 1]);
			aex1[j][i] = min(aex1[j][i - 1], aex1[j + (1 << (i - 1))][i - 1]);
			aex2[j][i] = max(aex2[j][i - 1], aex2[j + (1 << (i - 1))][i - 1]);
		}
	for (int i = 1; i <= 20; i++)
		for (int j = 1; j + (1 << i) - 1 <= m; j++) {
			bmax[j][i] = max(bmax[j][i - 1], bmax[j + (1 << (i - 1))][i - 1]);
			bmin[j][i] = min(bmin[j][i - 1], bmin[j + (1 << (i - 1))][i - 1]);
		}
}
pair<int, int> queryA(int l, int r) {
	int k = __lg(r - l + 1);
	int maxn = max(amax[l][k], amax[r - (1 << k) + 1][k]);
	int minn = min(amin[l][k], amin[r - (1 << k) + 1][k]);
	return make_pair(maxn, minn);
}
pair<int, int> queryB(int l, int r) {
	int k = __lg(r - l + 1);
	int maxn = max(bmax[l][k], bmax[r - (1 << k) + 1][k]);
	int minn = min(bmin[l][k], bmin[r - (1 << k) + 1][k]);
	return make_pair(maxn, minn);
}
int exA1(int l, int r) {
	int k = __lg(r - l + 1);
	return min(aex1[l][k], aex1[r - (1 << k) + 1][k]);
}
int exA2(int l, int r) {
	int k = __lg(r - l + 1);
	return max(aex2[l][k], aex2[r - (1 << k) + 1][k]);
}
int judge(int opt, int l, int r) {
	pair<int, int> res;
	if (opt == 1) res = queryA(l, r);
	else res = queryB(l, r);
	if (res.second < 0 && res.first > 0) return 0; // negative -> positive
	if (res.second <= 0 && res.first <= 0) return 1; // negative
	return 2; // positive
}
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> m >> q;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= m; i++) cin >> b[i];
	init();
	for (int i = 1; i <= q; i++) {
		static int l1, r1, l2, r2, ans;
		cin >> l1 >> r1 >> l2 >> r2;
		int typeA = judge(1, l1, r1);
		int typeB = judge(2, l2, r2);
		int Aex1 = exA1(l1, r1), Aex2 = exA2(l1, r1);
		int Amax = queryA(l1, r1).first, Amin = queryA(l1, r1).second;
		int Bmax = queryB(l2, r2).first, Bmin = queryB(l2, r2).second;
		if (typeA == 0 && typeB == 0) ans = max(Aex1 * Bmin, Aex2 * Bmax);
		if (typeA == 0 && typeB == 1) ans = Amin * Bmax;
		if (typeA == 0 && typeB == 2) ans = Amax * Bmin;
		if (typeA == 1 && typeB == 0) ans = Amax * Bmax;
		if (typeA == 1 && typeB == 1) ans = Amin * Bmax;
		if (typeA == 1 && typeB == 2) ans = Amax * Bmax;
		if (typeA == 2 && typeB == 0) ans = Amin * Bmin;
		if (typeA == 2 && typeB == 1) ans = Amin * Bmin;
		if (typeA == 2 && typeB == 2) ans = Amax * Bmin;
		cout << ans << '\n';
	}
	return 0;
}

T3 星战

题目描述

在这一轮的星际战争中，我方在宇宙中建立了 \(n\) 个据点，以 \(m\) 个单向虫洞连接。我们把终点为据点 \(u\) 的所有虫洞归为据点 \(u\) 的虫洞。

战火纷飞之中这些虫洞很难长久存在，敌人的打击随时可能到来。这些打击中的有效打击可以分为两类：

敌人会摧毁某个虫洞，这会使它连接的两个据点无法再通过这个虫洞直接到达，但这样的打击无法摧毁它连接的两个据点。
敌人会摧毁某个据点，由于虫洞的主要技术集中在出口处，这会导致该据点的所有还未被摧毁的虫洞被一同摧毁。而从这个据点出发的虫洞则不会摧毁。

注意：摧毁只会导致虫洞不可用，而不会消除它的存在。

为了抗击敌人并维护各部队和各据点之间的联系，我方发展出了两种特种部队负责修复虫洞：

A 型特种部队则可以将某个特定的虫洞修复。
B 型特种部队可以将某据点的所有损坏的虫洞修复。

考虑到敌人打击的特点，我方并未在据点上储备过多的战略物资。因此只要这个据点的某一条虫洞被修复，处于可用状态，那么这个据点也是可用的。

我方掌握了一种苛刻的空间特性，利用这一特性我方战舰可以沿着虫洞瞬移到敌方阵营，实现精确打击。

为了把握发动反攻的最佳时机，指挥部必须关注战场上的所有变化，为了寻找一个能够进行反攻的时刻。总指挥认为：

如果从我方的任何据点出发，在选择了合适的路线的前提下，可以进行无限次的虫洞穿梭（可以多次经过同一据点或同一虫洞），那么这个据点就可以实现反击。
为了使虫洞穿梭的过程连续，尽量减少战舰在据点切换虫洞时的质能损耗，当且仅当只有一个从该据点出发的虫洞可用时，这个据点可以实现连续穿梭。
如果我方所有据点都可以实现反击，也都可以实现连续穿梭，那么这个时刻就是一个绝佳的反攻时刻。

总司令为你下达命令，要求你根据战场上实时反馈的信息，迅速告诉他当前的时刻是否能够进行一次反攻。

输入格式

输入的第一行包含两个正整数 \(n,m\)。

接下来 \(m\) 行每行两个数 \(u,v\)，表示一个从据点 \(u\) 出发到据点 \(v\) 的虫洞。保证 \(u \ne v\)，保证不会有两条相同的虫洞。初始时所有的虫洞和据点都是完好的。

接下来一行一个正整数 \(q\) 表示询问个数。

接下来 \(q\) 行每行表示一次询问或操作。首先读入一个正整数 \(t\) 表示指令类型：

若 \(t = 1\)，接下来两个整数 \(u, v\) 表示敌人摧毁了从据点 \(u\) 出发到据点 \(v\) 的虫洞。保证该虫洞存在且未被摧毁。
若 \(t = 2\)，接下来一个整数 \(u\) 表示敌人摧毁了据点 \(u\)。如果该据点的虫洞已全部被摧毁，那么这次袭击不会有任何效果。
若 \(t = 3\)，接下来两个整数 \(u, v\) 表示我方修复了从据点 \(u\) 出发到据点 \(v\) 的虫洞。保证该虫洞存在且被摧毁。
若 \(t = 4\)，接下来一个整数 \(u\) 表示我方修复了据点 \(u\)。如果该据点没有被摧毁的虫洞，那么这次修复不会有任何效果。

在每次指令执行之后，你需要判断能否进行一次反攻。如果能则输出 YES 否则输出 NO。

输出格式

输出一共 \(q\) 行。对于每个指令，输出这个指令执行后能否进行反攻。

样例 #1

样例输入 #1

样例输出 #1

NO
NO
YES
NO
YES
NO
NO
NO
YES
NO
NO

提示

【样例解释 #1】

虫洞状态可以参考下面的图片, 图中的边表示存在且未被摧毁的虫洞：

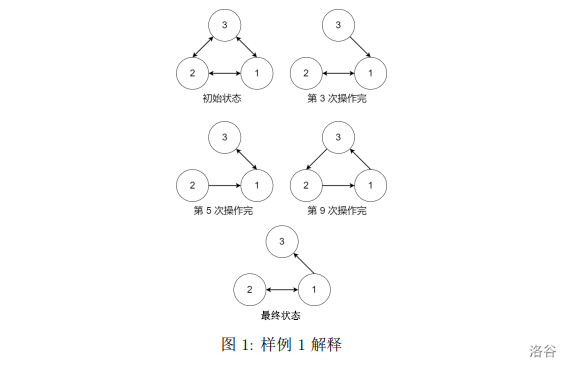
【样例 #2】

见附件中的 galaxy/galaxy2.in 与 galaxy/galaxy2.ans。

【样例 #3】

见附件中的 galaxy/galaxy3.in 与 galaxy/galaxy3.ans。

【样例 #4】

见附件中的 galaxy/galaxy4.in 与 galaxy/galaxy4.ans。

【数据范围】

对于所有数据保证：\(1 \le n \le 5 \times {10}^5\)，\(1 \le m \le 5 \times {10}^5\)，\(1 \le q \le 5 \times {10}^5\)。

测试点	\(n \le\)	\(m \le\)	\(q \le\)	特殊限制
\(1 \sim 3\)	\(10\)	\(20\)	\(50\)	无
\(4 \sim 8\)	\({10}^3\)	\({10}^4\)	\({10}^3\)	无
\(9 \sim 10\)	\(5 \times {10}^5\)	\(5 \times {10}^5\)	\(5 \times {10}^5\)	保证没有 \(t = 2\) 和 \(t = 4\) 的情况
\(11 \sim 12\)	\(5 \times {10}^5\)	\(5 \times {10}^5\)	\(5 \times {10}^5\)	保证没有 \(t = 4\) 的情况
\(13 \sim 16\)	\({10}^5\)	\(5 \times {10}^5\)	\(5 \times {10}^5\)	无
\(17 \sim 20\)	\(5 \times {10}^5\)	\(5\times 10^5\)	\(5 \times {10}^5\)	无

Solution

赛场上感觉脑子被宇宙射线轰了，完全没看出来两个条件其实是相同的。

其实这道题看出来两个条件是相同的过后就离答案不远了。既然两种条件是相同的，那就只维护出度为 \(1\) 即可，一种 60 分的思路是用 set 维护边，对于修改操作的时候暴力操作，然后只要每个出度都为 \(1\) 就是可行的。但是有一个更好的 Trick，叫做 Hash，具体思想就是给每一个点赋一个随机的权值，然后判断 \(\displaystyle\sum\limits_{i=1}^n Deg_i\times val_i=\sum\limits_{i=1}^nval_i\) 即可。对于 \(1,3\) 操作就直接修改就行了，\(2,4\) 操作需要预处理出来所有到达当前点的点的权值和。

这么一看这道题也是一个水题，可惜不知道这个 Trick。。

赛时 40 分。

#include<bits/stdc++.h>
#define ULOOP(i, x, y) for (int i = (x); i <= (y); i++)
#define DLOOP(i, x, y) for (int i = (x); i >= (y); i--)
using namespace std;
constexpr int _SIZE = 5e5;
int n, m, q;
long long val[_SIZE + 5], allHash, eHash[_SIZE + 5], totHash, ori[_SIZE + 5];
mt19937 Random(time(0));
long long destroyed[_SIZE + 5];
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    srand(114514);
    cin >> n >> m;
    ULOOP (i, 1, n) val[i] = Random(), allHash ^= val[i];
    ULOOP (i, 1, m) {
        static int u, v;
        cin >> u >> v;
        eHash[v] ^= val[u];
        totHash ^= val[u];
        ori[v] ^= val[u];
    }
    cin >> q;
    ULOOP (i, 1, q) {
        static int opt, x, y;
        cin >> opt >> x;
        if (opt == 1 || opt == 3) { // 其实不应该用异或，但是这样洛谷上照样可以过就很离谱，因为异或会导致出度为 3 与出度为 1 的情况贡献的权值相同
            cin >> y;
            totHash ^= val[x];
            eHash[y] ^= val[x];
            destroyed[y] ^= val[x];
        } else if (opt == 2) {
            totHash ^= eHash[x];
            eHash[x] = 0, destroyed[x] = ori[x];
        } else {
            totHash ^= destroyed[x];
            destroyed[x] = 0, eHash[x] = ori[x];
        }
        if (totHash == allHash) cout << "YES" << '\n';
        else cout << "NO" << '\n';
    }
    return 0;
}

posted @ 2022-11-01 08:30 Hanx16Msgr 阅读(231) 评论(0) 编辑收藏举报

刷新页面返回顶部

一个蒟蒻的学习笔记

欢迎神犇！！！

CSP-S 2022 T1~T3 题解

T1 假期计划

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

Solution

T2 策略游戏

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

Solution

T3 星战

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

Solution

公告