CF708E Student's Camp

Student's Camp

Codeforces 708E

Luogu CF708E

题面翻译

有一个 $(n+2)\times m$ 的网格。

除了第一行和最后一行，其他每一行每一天最左边和最右边的格子都有 $p$ 的概率消失。

求 $k$ 天后，网格始终保持连通的概率。

$n,m\le 1.5\times {10}^3$，$k\le {10}^5$，答案对 ${10}^9+7$ 取模。

题目描述

Alex studied well and won the trip to student camp Alushta, located on the seashore.

Unfortunately, it's the period of the strong winds now and there is a chance the camp will be destroyed! Camp building can be represented as the rectangle of $n+2$ concrete blocks height and $m$ blocks width.

Every day there is a breeze blowing from the sea. Each block, except for the blocks of the upper and lower levers, such that there is no block to the left of it is destroyed with the probability 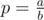. Similarly, each night the breeze blows in the direction to the sea. Thus, each block (again, except for the blocks of the upper and lower levers) such that there is no block to the right of it is destroyed with the same probability $p$ . Note, that blocks of the upper and lower level are indestructible, so there are only $n·m$ blocks that can be destroyed.

The period of the strong winds will last for $k$ days and $k$ nights. If during this period the building will split in at least two connected components, it will collapse and Alex will have to find another place to spend summer.

Find the probability that Alex won't have to look for other opportunities and will be able to spend the summer in this camp.

输入格式

The first line of the input contains two integers $n$ and $m$ ( $1<=n,m<=1500$ ) that define the size of the destructible part of building.

The second line of the input contains two integers $a$ and $b$ ( $1<=a<=b<={10}^9$ ) that define the probability $p$ . It's guaranteed that integers $a$ and $b$ are coprime.

The third line contains a single integer $k$ ( $0<=k<=100000$ ) — the number of days and nights strong wind will blow for.

输出格式

Consider the answer as an irreducible fraction is equal to . Print one integer equal to 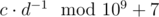. It's guaranteed that within the given constraints .

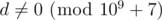样例 #1

样例输入 #1

2 2
1 2
1

样例输出 #1

937500007

样例 #2

样例输入 #2

5 1
3 10
1

样例输出 #2

95964640

样例 #3

样例输入 #3

3 3
1 10
5

样例输出 #3

927188454

提示

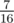In the first sample, each of the four blocks is destroyed with the probability . There are $7$ scenarios that result in building not collapsing, and the probability we are looking for is equal to , so you should print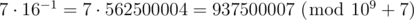

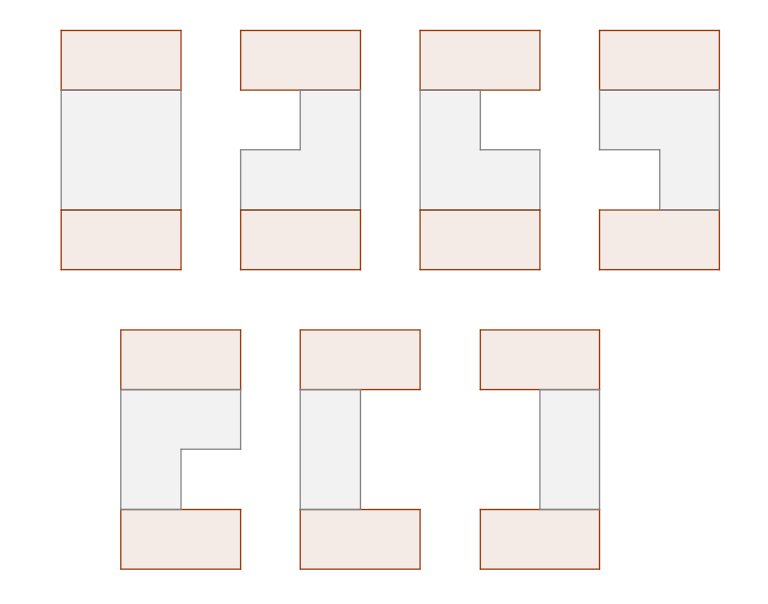
Solution

一道神仙前缀和优化概率 $\mathtt{\text{DP}}$ 题。

先定义 $D(i)$ 表示 $k$ 次吹风中刚好成功了 $i$ 次的概率。那么 $D(i)$ 很好计算：

$$D(i)=\left(\begin{array}{c}k\\ i\end{array}\right)\cdot p^i\cdot (1-p{)}^{k-i}$$

显然 $D(i)$ 是可以预处理出来的。

因为我们要求的东西是与每一层的区间相关的，所以不如再定义一个 $P(l,r)$ 表示一层中吹风吹的只剩 $(l,r)$ 的概率，那么用前面的 $D$ 就很好表示：

$$P(l,r)=D(l-1)\cdot D(m-r)$$

那么由此引出设计的状态：定义 $f(i,l,r)$ 表示第 $i$ 层被吹风吹的只剩下 $[l,r]$ 的概率。因为墙不能悬空，所以转移的时候 $i-1$ 层的区间一定要与 $[l,r]$ 有交，那么推出 $f(i,l,r)$ 的转移方程：

$$f(i,l,r)=P(l,r)\cdot \sum _{[l^{\prime },r^{\prime }]\cap [l,r]\ne \varnothing }f(i-1,l^{\prime },r^{\prime })$$

这样求解的话不难发现转移是 $\mathcal{O}(m^2)$ 的，所以需要优化。

考虑容斥，与 $[l,r]$ 有交的部分就可以表示成为所有区间减去那些没有交的区间。根据这个想法，将原式子变形。

$$f(i,l,r)=P(l,r)\cdot (\sum _{l^{\prime }\le r^{\prime }}f(i-1,l^{\prime },r^{\prime })-\sum _{r^{\prime }<l}f(i-1,l^{\prime },r^{\prime })-\sum _{l^{\prime }>r}f(i-1,l^{\prime },r^{\prime }))$$

将三个带有求和号的部分重新定义一下：

$$F(i)=\sum _{l\le r}f(i,l,r)$$

$$L(i,x)=\sum _{r<x}f(i,l,r)$$

$$R(i,x)=\sum _{l>x}f(i,l,r)$$

那么可以改写一下 $f(i,l,r)$ 的转移：

$$f(i,l,r)=P(l,r)\cdot (F(i-1)-L(i-1,l)-R(i-1,r))$$

现在来看怎么转移 $F,L,R$。容易发现，$L,R$ 其实是对称的，所以可以有 $L(i,x)=R(i,m-x+1)$。为了求出 $L$，再定义一个 $S(i,r)={\displaystyle \sum _{l\le r}f(i,l,r)}$。根据 $S$ 可以计算出 $F,L$：

$$F(i)=\sum _{x\le m}S(i,x)$$

$$L(i,x)=\sum _{r<x}S(i,r)$$

其实可以发现：$F(i)=L(i,m+1)$。

考虑怎么计算 $S$，将上面的定义式进行变形：

$$\begin{array}{lll}S(i,r)& =& {\displaystyle \sum _{l\le r}f(i,l,r)}\\ & =& {\displaystyle \sum _{l\le r}P(l,r)\cdot (F(i-1)-L(i-1,l)-R(i-1,r))}\\ & =& D(m-r)\cdot {\displaystyle \sum _{l\le r}D(l-1)\cdot (F(i-1)-L(i-1)-R(i-1))}\\ & =& D(m-r)\cdot (F(i-1)-R(i-1,r)){\displaystyle \sum _{l\le r}D(l-1)-\sum _{l\le r}D(l-1)\cdot L(i-1,l)}\end{array}$$

发现此时的 ${\displaystyle \sum _{l\le r}D(l-1)}$ 和 ${\displaystyle \sum _{l\le r}D(l-1)\cdot L(i-1,l)}$ 已经独立，所以可以对这两个式子维护前缀和，然后就可以实现对 $S$ 的 $\mathcal{O}(1)$ 转移。

总时间复杂度为 $\mathcal{O}(nm)$。

#include<bits/stdc++.h>
#define int long long
using namespace std;
constexpr int _SIZE = 1.5e3, mod = 1e9 + 7, _MAXN = 1e5;
int Qpow(int x, int y) {
    int res = 1, base = x % mod;
    while (y) {
        if (y & 1) res = res * base % mod;
        y >>= 1, base = base * base % mod;
    }
    return res;
}
int F[2], D[_MAXN + 5], R[2][_SIZE + 5], L[2][_SIZE + 5], S[2][_SIZE + 5];
int sum1[_SIZE + 5], sum2[_SIZE + 5];
int p, fac[_MAXN + 5], inv[_MAXN + 5];
int n, k, m, a, b;
int cur = 1, last = 0;
void init() {
    fac[0] = 1; inv[0] = 1;
    for (int i = 1; i <= k; i++) fac[i] = fac[i - 1] * i % mod, inv[i] = Qpow(fac[i], mod - 2);
}
int C(int x, int y) {
    return fac[x] * inv[y] % mod * inv[x - y] % mod;
}
void initD() {
    for (int i = 0; i <= k; i++) 
        D[i] = C(k, i) * Qpow(p, i) % mod * Qpow(mod + 1 - p, k - i) % mod;
    sum1[0] = D[0];
    for (int i = 1; i <= m; i++) sum1[i] = (sum1[i - 1] + D[i]) % mod;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    cin >> n >> m;
    cin >> a >> b; p = a * Qpow(b, mod - 2) % mod;
    cin >> k;
    init(); initD();
    S[cur][m] = 1; F[cur] = 1;
    for (int i = 1; i <= n; i++) {
        swap(cur, last);
        sum2[0] = 0;
        for (int j = 1; j <= m + 1; j++) (sum2[j] = sum2[j - 1] + D[j - 1] * L[last][j] % mod) %= mod;
        for (int r = 1; r <= m; r++) {
            S[cur][r] = D[m - r] * (((F[last] - R[last][r] + mod) % mod * sum1[r - 1] % mod - sum2[r] + mod) % mod) % mod;
        }
        for (int j = 1; j <= m + 1; j++) (L[cur][j] = L[cur][j - 1] + S[cur][j - 1]) %= mod, R[cur][m - j + 1] = L[cur][j];
        F[cur] = L[cur][m + 1];
    }
    cout << F[cur] << '\n';
    return 0;
}