P1231 教辅的组成
教辅的组成
题目背景
滚粗了的 HansBug 在收拾旧语文书，然而他发现了什么奇妙的东西。
题目描述
蒟蒻 HansBug 在一本语文书里面发现了一本答案，然而他却明明记得这书应该还包含一份练习题。然而出现在他眼前的书多得数不胜数，其中有书，有答案，有练习册。已知一个完整的书册均应该包含且仅包含一本书、一本练习册和一份答案，然而现在全都乱做了一团。许多书上面的字迹都已经模糊了，然而 HansBug 还是可以大致判断这是一本书还是练习册或答案，并且能够大致知道一本书和答案以及一本书和练习册的对应关系（即仅仅知道某书和某答案、某书和某练习册有可能相对应，除此以外的均不可能对应）。既然如此，HansBug 想知道在这样的情况下，最多可能同时组合成多少个完整的书册。
输入格式
第一行包含三个正整数 \(N_1\)、\(N_2\)、\(N_3\)，分别表示书的个数、练习册的个数和答案的个数。
第二行包含一个正整数 \(M_1\)，表示书和练习册可能的对应关系个数。
接下来 \(M_1\) 行每行包含两个正整数 \(x\)、\(y\)，表示第 \(x\) 本书和第 \(y\) 本练习册可能对应。（\(1\)\(\leq\)\(x\)\(\leq\)\(N_1\)，\(1\)\(\leq\)\(y\)\(\leq\)\(N_2\)）
第 \(M_{1+3}\) 行包含一个正整数 \(M_2\)，表述书和答案可能的对应关系个数。
接下来 \(M_2\) 行每行包含两个正整数 \(x\)、\(y\)，表示第 \(x\) 本书和第 \(y\) 本答案可能对应。（\(1\)\(\leq\)\(x\)\(\leq\)\(N_1\)，\(1\)\(\leq\)\(y\)\(\leq\)\(N_3\)）
输出格式
输出包含一个正整数，表示最多可能组成完整书册的数目。
样例 #1
样例输入 #1
5 3 4
5
4 3
2 2
5 2
5 1
5 3
5
1 3
3 1
2 2
3 3
4 3
样例输出 #1
2
提示
样例说明：
如题，\(N_1=5\)，\(N_2=3\)，\(N_3=4\)，表示书有 \(5\) 本、练习册有 \(3\) 本、答案有 \(4\) 本。
\(M_1=5\)，表示书和练习册共有 \(5\) 个可能的对应关系，分别为：书 4 和练习册 3、书 2 和练习册 2、书 5 和练习册 2、书 5 和练习册 1 以及书 5 和练习册 3。
\(M_2=5\)，表示数和答案共有 \(5\) 个可能的对应关系，分别为：书 1 和答案 3、书 3 和答案 1、书 2 和答案 2、书 3 和答案 3 以及书 4 和答案 3。
所以，以上情况的话最多可以同时配成两个书册，分别为：书 2 + 练习册 2 + 答案 2、书 4 + 练习册 3 + 答案 3。
数据规模：
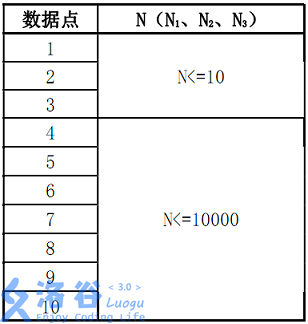
对于数据点 \(1\), \(2\), \(3\)，\(M_1\), \(M_2\leq 20\)
对于数据点 \(4-10\)，\(M_1\), \(M_2 \leq 20000\)
Solution
看到这类的求最大匹配的问题，很容易可以想到建图然后用网络流来解决，可以很轻松地建出这个图（样例）：
但这样不难发现会出现一本书搭配了多本练习册和答案这种情况，与题目条件不符。解决方法就是将中间的书拆点并在中间连一条容量为 \(1\) 的边即可。
最后对这张图跑一个dinic算法即可。
Code
需要注意建图的问题，并且边的数量不止 \(4e4\)，需要开的更大，否则会导致 RE。
#include<bits/stdc++.h>
using namespace std;
template<typename T> void read(T &k)
{
k=0;T flag=1;char b=getchar();
while (!isdigit(b)) {flag=(b=='-')?-1:1;b=getchar();}
while (isdigit(b)) {k=k*10+b-48;b=getchar();}
k*=flag;
}
template<typename T> void write(T k) {if (k<0) putchar('-'),write(-k);if (k>9) write(k/10);putchar(k%10+48);}
template<typename T> void writewith(T k,char c) {write(k);putchar(c);}
const int _SIZE=1e4;
int S,T;
int n1,n2,n3,m1,m2;
struct EDGE{
int nxt,to,len;
}edge[(_SIZE<<5)+5];
int tot=1,head[(_SIZE<<2)+5],cur[(_SIZE<<2)+5],dist[(_SIZE<<2)+5];
int id(int x,int v)
{
int ind[6]={0,0,n2,n2+n1,n2+n1+n1};
return ind[x]+v;
}
void AddEdge(int x,int y,int len)
{
edge[++tot]=(EDGE){head[x],y,len};
head[x]=tot;
edge[++tot]=(EDGE){head[y],x,0};
head[y]=tot;
}
bool bfs()
{
queue<int> q;
q.push(S);
memset(dist,-1,sizeof(dist));
dist[S]=0;
while (!q.empty())
{
int u=q.front();q.pop();
for (int i=head[u];i;i=edge[i].nxt)
{
int twd=edge[i].to;
if (dist[twd]!=-1 || edge[i].len<=0) continue;
q.push(twd);
dist[twd]=dist[u]+1;
if (twd==T) return 1;
}
}
return 0;
}
int dfs(int x,int f)
{
if (f==0 || x==T) return f;
int used=0;
for (int &i=cur[x];i;i=edge[i].nxt)
{
int twd=edge[i].to;
if (edge[i].len && dist[twd]==dist[x]+1)
{
int w=dfs(twd,min(f,edge[i].len));
if (!w) continue;
used+=w,f-=w;
edge[i].len-=w,edge[i^1].len+=w;
if (f==0) break;
}
}
if (!used) dist[x]=-1;
return used;
}
int dinic()
{
int mflow=0;
while (bfs())
{
memcpy(cur,head,sizeof(head));
mflow+=dfs(S,INT_MAX);
}
return mflow;
}
int main()
{
read(n1),read(n2),read(n3);
S=n2+n1*2+n3+1;T=S+1;
read(m1);
for (int i=1;i<=m1;i++)
{
int u,v;read(u),read(v);
AddEdge(id(1,v),id(2,u),1);
}
read(m2);
for (int i=1;i<=m2;i++)
{
int u,v;read(u),read(v);
AddEdge(id(3,u),id(4,v),1);
}
for (int i=1;i<=n1;i++) AddEdge(id(2,i),id(3,i),1);
for (int i=1;i<=n2;i++) AddEdge(S,id(1,i),1);
for (int i=1;i<=n3;i++) AddEdge(id(4,i),T,1);
int ans=dinic();
writewith(ans,'\n');
return 0;
}
