CF722E Research Rover
Research Rover
题面翻译
有一个n*m的网格图,图中有k个特殊点。
初始时你有一个权值s,并且只能向下或向右走,
每经过一个特殊点会使得你的权值/2(向上取整)。
求从(1,1)走到(n,m)时拥有权值的期望(mod 1e9+7)。
题目描述
Unfortunately, the formal description of the task turned out to be too long, so here is the legend.
Research rover finally reached the surface of Mars and is ready to complete its mission. Unfortunately, due to the mistake in the navigation system design, the rover is located in the wrong place.
The rover will operate on the grid consisting of
The rover is currently located at cell
The cargo section of the rover contains the battery required to conduct the research. Initially, the battery charge is equal to
Some of the cells contain anomaly. Each time the rover gets to the cell with anomaly, the battery looses half of its charge rounded down. Formally, if the charge was equal to 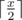 .
.
While the rover picks a random shortest path to proceed, compute the expected value of the battery charge after it reaches cell
输入格式
The first line of the input contains four integers
The follow
输出格式
The answer can always be represented as an irreducible fraction 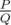 . Print the only integer
. Print the only integer
样例 #1
样例输入 #1
3 3 2 11
2 1
2 3
样例输出 #1
333333342
样例 #2
样例输入 #2
4 5 3 17
1 2
3 3
4 1
样例输出 #2
514285727
样例 #3
样例输入 #3
1 6 2 15
1 1
1 5
样例输出 #3
4
提示
In the first sample, the rover picks one of the following six routes:
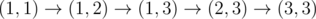 , after passing cell
, after passing cell 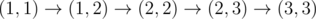 , after passing cell
, after passing cell 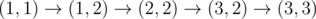 , charge remains unchanged and equals
, charge remains unchanged and equals 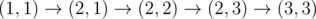 , after passing cells
, after passing cells 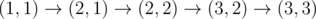 , after passing cell
, after passing cell 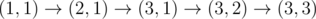 , after passing cell
, after passing cell
Expected value of the battery charge is calculated by the following formula:
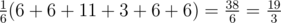 .
.
Thus
Solution
模拟赛的 T4,赛时就写了个
首先先来想一想最基础的东西:在
如果将这张表格顺时针旋转
注意题目的数据范围,因为
先考虑计算从起点出发不经过其他特殊点到达第
解释下方程的含义:先计算出不做任何限制到达第
那么根据这种做法,可以推广到从起点出发恰好经过
同样来解释方程的含义:与上面的方程类似,先计算出不做任何限制到达第
此外需要注意的是,因为需要从起点出发并到达终点,所以在起点和终点不是特殊点的时候将这俩加入特殊点,并且在统计答案的时候还有另外需要注意的(待会代码注释里会讲)。因为
计算组合数和答案的时候要用到除法,所以需要计算逆元,用费马小定理计算即可。需要知道的是,组合数计算的时候用到的逆元都是某个数阶乘的逆元,所以这部分的逆元可以预处理来减多一个
还有一些小细节会在代码中提到。
Code
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof a)
#define int long long
using namespace std;
template<typename T> void read(T &k)
{
k=0;T flag=1;char b=getchar();
while (!isdigit(b)) {flag=(b=='-')?-1:1;b=getchar();}
while (isdigit(b)) {k=k*10+b-48;b=getchar();}
k*=flag;
}
void write(int x) {if (x<0) putchar('-'),write(-x);if (x>9) write(x/10);putchar(x%10+'0');}
void writewith(int x,char c) {write(x);putchar(c);}//快读快输模板
const int barrierSize=2000,mod=1e9+7,mapSize=1e5;
int n,m,k,S;
struct POINT{//存点,按照x,y的顺序排序
int x,y;
bool operator<(const POINT &a) const {return (x!=a.x)?x<a.x:y<a.y;}
}bar[barrierSize+5];
int Fpow(int x,int y)//快速幂,用于求逆元
{
int res=1,base=x%mod;
while (y)
{
if (y&1) res=res*base%mod;
base=base*base%mod,y>>=1;
}
return res;
}
int Inv[(mapSize<<1)+5];
int inv(int x) {return Inv[x];}
int fac[(mapSize<<1)+5];
void preWork()//预处理阶乘和逆元
{
fac[0]=1;
for (int i=1;i<=(mapSize<<1);i++) fac[i]=fac[i-1]*i%mod;//阶乘
Inv[mapSize-1]=Fpow(fac[mapSize-1],mod-2);
for (int i=mapSize-1;i;i--) Inv[i-1]=Inv[i]*i%mod;//用递推的方法求阶乘的逆元,即Inv[i]表示i!的逆元
}
int C(int x,int y) {return fac[x]*inv(y)%mod *inv(x-y)%mod;}//计算组合数,直接调用提前计算好的阶乘和逆元即可
int way(POINT b,POINT a) {return C(a.x-b.x+a.y-b.y,a.x-b.x);}//计算从b到a的路径数
int f[barrierSize+5][barrierSize+5];//存答案,第二维可以只开到25
bool flag1=0,flag2=0;//flag1表示起点是否是特殊点,flag2表示终点是否是特殊点
signed main()
{
preWork();
read(n),read(m),read(k),read(S);
for (int i=1;i<=k;i++)
read(bar[i].x),read(bar[i].y),
flag1=(bar[i].x==1 && bar[i].y==1)?1:flag1,flag2=(bar[i].x==n && bar[i].y==m)?1:flag2;//维护flag1,flag2
if (!flag1) bar[++k]=(POINT){1,1};flag1^=1;//如果起点非特殊点,则加入特殊点内,flag1取反的含义在统计答案的时候会提
if (!flag2) bar[++k]=(POINT){n,m};flag2^=1;//将终点加入特殊点
sort(bar+1,bar+k+1);
int maxBar=ceil(log2(S))+1;//最大可能的j,直接取21也可以
int sum=0;
for (int i=1;i<=k;i++)
{
sum=0;//用于优化掉转移方程中的最后一部分
for (int j=1;j<=maxBar;j++)
{
f[i][j]=C(bar[i].x+bar[i].y-2,bar[i].x-1);//不加限制的总路径
for (int t=1;t<=i-1;t++)
if (bar[t].x<=bar[i].x && bar[t].y<=bar[i].y) f[i][j]=((f[i][j]-f[t][j]*way(bar[t],bar[i]))%mod+mod)%mod;//如果可以从t到i,那么就将这部分重复的减去
f[i][j]=((f[i][j]-sum)%mod+mod)%mod;//减去最后一部分,注意处理负数的情况
sum=(sum+f[i][j])%mod;//更新前缀和
}
}
int all=C(n+m-2,n-1),answer=0;//因为超过了log2(S)的部分的体力值都为1,所以这部分对答案的贡献就是这部分的方案数
for (int i=flag1+flag2;i<=maxBar;i++)//因为f[i][j]表示的是经过了j个特殊点的方案数,而我们将起点和终点给作为了特殊点处理,所以需要减去起点和终点多算的特殊点数量,这部分数量就是flag1+flag2
{
answer=(f[k][i]*S+answer)%mod;//计算总体力值,即方案数*对应体力值
S-=(S/2);//ceil(S/2)
all=((all-f[k][i])%mod+mod)%mod;//all用于统计体力值为1的部分对答案的贡献,所以需要将前面这部分的方案数减去
}
answer=(answer+all)%mod;//加上体力值为1的情况
writewith(answer*Fpow(C(n+m-2,n-1),mod-2)%mod,'\n');//需要注意的是总方案数的逆元是不能调用Inv数组的,因为Inv数组是阶乘的逆元,所以这里用快速幂重新算逆元来记录答案
return 0;
}
一道很有意思的题目,值得多想一想。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步