珂朵莉树/ODT/颜色段均摊
珂朵莉树/ODT/颜色段均摊
诞生于 CF896C (镜像站),最开始叫做老司机树(因为发现此数据结构的用户名叫 (珂朵莉是世界上最幸福的女孩)。
珂朵莉树一般适用于数据随机,且带有区间推平这类操作的问题,可以在快于线段树的时间内跑出正确答案(如果数据不随机的话也可以 T 到飞起)。
珂朵莉树的主要思想是将连续一段值相等的区间用一个三元组
建树
珂朵莉树的建立很简单,只需要用一个结构体 Node 存储三元组 set 中,以左端点为关键字定义
具体代码也很简单:
struct NODE{
int l,r;//左右端点
mutable int v;//区间值,具体根据题目而定
NODE (int l,int r=0,int v=0) : l(l),r(r),v(v) {}
bool operator< (const NODE &a) const {return l<a.l;}//重载<号
};
set <NODE> ctlt;//建树
这里使用了 mutable 这一关键字,使得 const 函数中也强制可以更改。这样就可以方便珂朵莉树的一些操作。
珂朵莉树最基础的操作有两个: split和assign 。
Split 操作
即分裂操作,将原有区间
首先需要在珂朵莉树中二分找到第一个左端点大于等于 set 自带的 lower_bound 函数即可解决。
找到这个区间后,如果
如果 ctlt.end() 即可。分裂时,直接将原区间从珂朵莉树中删除,添加
有一个小技巧, set 中的 insert 操作会返回一个二元组 pair ,这个 pair 的第一项就是插入的这个区间的迭代器,直接用 first 调用即可。
另外,感谢 C++14,现在我们可以用auto来代替set<NODE>::iterator 定义迭代器了。
auto split(int pos)
{
auto it=ctlt.lower_bound(NODE(pos));//找到区间的迭代器
if (it!=ctlt.end() && it->l==pos) return it;//如果pos是区间左端点直接返回当前区间迭代器
--it;//迭代器前移
if (it->r<pos) return ctlt.end();//不符合条件直接返回end()
int l=it->l,r=it->r,v=it->v;
ctlt.erase(it);//删除原区间
ctlt.insert(NODE(l,pos-1,v));//插入左区间
return ctlt.insert(NODE(pos,r,v)).first;//插入右区间并返回迭代器
}
Assign 操作
这一操作是降低珂朵莉树时间复杂度的最重要部分,在数据随机的情况下会出现大量 assign 操作,从而使得区间数量大概大概维持在 (我也不会证明)。
Assign 操作的意思是将一个区间的值直接推平。那么可以得知,如果需要推平的区间 split 操作,所以在 assign 开始时直接 split(l) 和 split(r+1) 。需要注意的是,必须先 split(r+1) 在 split(l) ,否则可能导致 split 操作返回的迭代器在 split(r+1) 失效,导致
实现起来也很简单, set 中提供的 erase 函数支持传入两个迭代器 itl 和 itr ,表示删除迭代器 itl 和 itr 之间的所有元素。所以在 split 操作时获取到 itl 和 itr ,然后直接 ctlt.erase(itl,itr) 即可。此时
代码很短:
void assign(int l,int r,int x)
{
auto itr=split(r+1),itl=split(l);//分裂区间,创造出区间[l,r]
ctlt.erase(itl,itr);//删除[l,r]之间的所有区间
ctlt.insert(NODE(l,r,x));//插入新的区间
}
这些就是珂朵莉树的基本操作,具体查询之类的根据题目来写。
下面结合珂朵莉树的最初题目来理解珂朵莉树的使用。
Willem, Chtholly and Seniorious
题面翻译
【题面】
请你写一种奇怪的数据结构,支持:
【输入格式】
这道题目的输入格式比较特殊,需要选手通过
输入一行四个整数
其中
数据生成的伪代码如下

其中上面的op指题面中提到的四个操作。
【输出格式】
对于每个操作3和4,输出一行仅一个数。
题目描述
— Willem...
— What's the matter?
— It seems that there's something wrong with Seniorious...
— I'll have a look...

Seniorious is made by linking special talismans in particular order.
After over 500 years, the carillon is now in bad condition, so Willem decides to examine it thoroughly.
Seniorious has
In order to maintain it, Willem needs to perform
There are four types of operations:
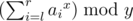 .
.
输入格式
The only line contains four integers
The initial values and operations are generated using following pseudo code:
def rnd():
ret = seed
seed = (seed * 7 + 13) mod 1000000007
return ret
for i = 1 to n:
a[i] = (rnd() mod vmax) + 1
for i = 1 to m:
op = (rnd() mod 4) + 1
l = (rnd() mod n) + 1
r = (rnd() mod n) + 1
if (l > r):
swap(l, r)
if (op == 3):
x = (rnd() mod (r - l + 1)) + 1
else:
x = (rnd() mod vmax) + 1
if (op == 4):
y = (rnd() mod vmax) + 1
Here
输出格式
For each operation of types
样例 #1
样例输入 #1
10 10 7 9
样例输出 #1
2
1
0
3
样例 #2
样例输入 #2
10 10 9 9
样例输出 #2
1
1
3
3
提示
In the first example, the initial array is
The operations are:
Solution
首先可以得知题目的数据是随机分布的,并且出现了区间推平的操作,所以就可以使用珂朵莉树来解决。
2 操作就是珂朵莉树最基础的操作,就不再讲了。
1 操作与 assign 操作类似,先将
void add(int l,int r,int x)
{
auto itr=split(r+1),itl=split(l);//分裂
for (auto it=itl;it!=itr;it++)//遍历[l,r]的所有区间
it->v+=x;//修改v值
}
然后是 3 操作,要求求出区间第 vector 中,然后根据区间值
struct RANK{//用结构体存储区间值以及区间长度
int num,cnt;
bool operator<(const RANK &a) const{
return num<a.num;
}
};
int RankQuery(int l,int r,int x)
{
auto itr=split(r+1),itl=split(l);
vector<RANK> v;
for (auto it=itl;it!=itr;it++)
v.push_back((RANK){it->v,it->r - it->l +1});//将区间值以及区间长度存入vector
sort(v.begin(),v.end());//对vector排序
for (auto it:v)//遍历vector
{
if (it.cnt<x) x-=it.cnt;//总数量不够x
else return it.num;//够了就返回当前区间值
}
}
最后是 4 操作,要求求出区间
int Fpow(int x,int y,int p)//快速幂模板
{
int res=1,base=x%p;
while (y)
{
if (y&1) res=res*base%p;
base=base*base%p;
y>>=1;
}
return res;
}
int PowerQuery(int l,int r,int x,int y)
{
auto itr=split(r+1),itl=split(l);
int res=0;
for (auto it=itl;it!=itr;it++)
res=(res+Fpow(it->v,x,y)*(it->r - it->l +1)%y)%y;//区间[l,r,v]的区间x次幂和为v的x次幂乘上区间长度
return res;
}
最后放上总代码:(各部分具体含义前面已经解释清楚了,所以就没写注释了)
#include<bits/stdc++.h>
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
using namespace std;
template<typename T> void read(T &k)
{
k=0;T flag=1;char b=getchar();
while (!isdigit(b)) {flag=(b=='-')?-1:1;b=getchar();}
while (isdigit(b)) {k=k*10+b-48;b=getchar();}
k*=flag;
}
struct NODE{
int l,r;
mutable int v;
NODE (int l,int r=0,int v=0) : l(l),r(r),v(v) {}
bool operator< (const NODE &a) const {return l<a.l;}
};
set <NODE> ctlt;
auto split(int pos)
{
auto it=ctlt.lower_bound(NODE(pos));
if (it!=ctlt.end() && it->l==pos) return it;
--it;
if (it->r<pos) return ctlt.end();
int l=it->l,r=it->r,v=it->v;
ctlt.erase(it);
ctlt.insert(NODE(l,pos-1,v));
return ctlt.insert(NODE(pos,r,v)).first;
}
void assign(int l,int r,int x)
{
auto itr=split(r+1),itl=split(l);
ctlt.erase(itl,itr);
ctlt.insert(NODE(l,r,x));
}
void add(int l,int r,int x)
{
auto itr=split(r+1),itl=split(l);
for (auto it=itl;it!=itr;it++)
it->v+=x;
}
struct RANK{
int num,cnt;
bool operator<(const RANK &a) const{
return num<a.num;
}
};
int RankQuery(int l,int r,int x)
{
auto itr=split(r+1),itl=split(l);
vector<RANK> v;
for (auto it=itl;it!=itr;it++)
v.push_back((RANK){it->v,it->r - it->l +1});
sort(v.begin(),v.end());
for (auto it:v)
{
if (it.cnt<x) x-=it.cnt;
else return it.num;
}
}
int Fpow(int x,int y,int p)
{
int res=1,base=x%p;
while (y)
{
if (y&1) res=res*base%p;
base=base*base%p;
y>>=1;
}
return res;
}
int PowerQuery(int l,int r,int x,int y)
{
auto itr=split(r+1),itl=split(l);
int res=0;
for (auto it=itl;it!=itr;it++)
res=(res+Fpow(it->v,x,y)*(it->r - it->l +1)%y)%y;
return res;
}
int n,m,seed,vmax;
const int MOD=1e9+7;
int rnd()
{
int ret=seed;
seed=(seed*7+13)%MOD;
return ret;
}
signed main()
{
read(n),read(m),read(seed),read(vmax);
for (int i=1;i<=n;i++)
{
int v=rnd()%vmax+1;
ctlt.insert(NODE(i,i,v));
}
for (int i=1;i<=m;i++)
{
int op=rnd()%4+1,l=rnd()%n+1,r=rnd()%n+1,x,y;
if (l>r) swap(l,r);
if (op==3) x=(rnd()%(r-l+1))+1;
else x=(rnd()%vmax)+1;
if (op==4) y=rnd()%vmax+1;
if (op==1) add(l,r,x);
if (op==2) assign(l,r,x);
if (op==3) printf("%lld\n",RankQuery(l,r,x));
if (op==4) printf("%lld\n",PowerQuery(l,r,x,y));
}
return 0;
}
代码的时间复杂度大概在
说实话我没看出来珂朵莉树与树有什么关系,珂朵莉树算是一种优雅的暴力,在特殊情况下用来骗一骗分还是足够用的。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步