RANSAC的基本原理（最小二乘法拟合的改进版）

转载：https://zhuanlan.zhihu.com/p/62238520

RANSAC简介

RANSAC(RAndom SAmple Consensus,随机采样一致)算法是从一组含有“外点”(outliers)的数据中正确估计数学模型参数的迭代算法。“外点”一般指的的数据中的噪声，比如说匹配中的误匹配和估计曲线中的离群点。所以，RANSAC也是一种“外点”检测算法。RANSAC算法是一种不确定算法，它只能在一种概率下产生结果，并且这个概率会随着迭代次数的增加而加大（之后会解释为什么这个算法是这样的）。RANSAC算最早是由Fischler和Bolles在SRI上提出用来解决LDP(Location Determination Proble)问题的。

对于RANSAC算法来说一个基本的假设就是数据是由“内点”和“外点”组成的。“内点”就是组成模型参数的数据，“外点”就是不适合模型的数据。同时RANSAC假设：在给定一组含有少部分“内点”的数据，存在一个程序可以估计出符合“内点”的模型。

RANSAC 与最小二乘法的区别

从上述的内容我们可以得知其实这两个东西都是用来做拟合的，但是他们之间又有什么关系、有什么区别、应用场景有什么不同呢？

在实际开发或生产实践中，数据都会有一定的偏差，当我们已知两个变量之间的关系是线性回归函数，Y=aX+b，如果我们想知道具体的a和b的值，理论上说我们只需要两个点就能满足需求，但是由于误差的存在，我们任意选取的两个点所求出的a和b可能都不相同，我们最想要的就是最后的理论模型与测试值的误差最小

最小二乘法：通过计算最小均方差关于a和b的偏导数为0时的值，在很多情况下最小二乘法就是线性回归的代名词，但是它只适用于误差较小的情况
RANSAC：在模型已确定且最大迭代次数允许的情况下，RANSAC总是可以找到最优解（对于包含80%误差的数据集，RANSAC的效果远远好过最小二乘法）

综上所述我们可以片面地认为最小二乘法适用于误差小的情况，RANSAC使用与误差稍大且最大迭代次数允许的情况，在图像处理的实际开发中，由于一张图片的像素个数庞大，采用最小二乘法运算量巨大且计算速度很慢

算法基本思想和流程

RANSAC是通过反复选择数据集去估计出模型，一直迭代到估计出认为比较好的模型。
具体的实现步骤可以分为以下几步：

选择出可以估计出模型的最小数据集；(对于直线拟合来说就是两个点，对于计算Homography矩阵就是4个点)
使用这个数据集来计算出数据模型；
将所有数据带入这个模型，计算出“内点”的数目；(累加在一定误差范围内的适合当前迭代推出模型的数据)
比较当前模型和之前推出的最好的模型的“内点“的数量，记录最大“内点”数的模型参数和“内点”数；
重复1-4步，直到迭代结束或者当前模型已经足够好了(“内点数目大于一定数量”)。

迭代次数推导

这里有一点就是迭代的次数我们应该选择多大呢？这个值是否可以事先知道应该设为多少呢？还是只能凭经验决定呢？这个值其实是可以估算出来的。下面我们就来推算一下。

假设“内点”在数据中的占比为

那么我们每次计算模型使用

也就是说，在迭代

通过上式，可以求得

“内点”的概率

用Python实现直线拟合

import numpy as np
import matplotlib.pyplot as plt
import random
import math

# 数据量。
SIZE = 50
# 产生数据。np.linspace 返回一个一维数组，SIZE指定数组长度。
# 数组最小值是0，最大值是10。所有元素间隔相等。
X = np.linspace(0, 10, SIZE)
Y = 3 * X + 10

fig = plt.figure()
# 画图区域分成1行1列。选择第一块区域。
ax1 = fig.add_subplot(1,1, 1)
# 标题
ax1.set_title("RANSAC")


# 让散点图的数据更加随机并且添加一些噪声。
random_x = []
random_y = []
# 添加直线随机噪声
for i in range(SIZE):
    random_x.append(X[i] + random.uniform(-0.5, 0.5)) 
    random_y.append(Y[i] + random.uniform(-0.5, 0.5)) 
# 添加随机噪声
for i in range(SIZE):
    random_x.append(random.uniform(0,10))
    random_y.append(random.uniform(10,40))
RANDOM_X = np.array(random_x) # 散点图的横轴。
RANDOM_Y = np.array(random_y) # 散点图的纵轴。

# 画散点图。
ax1.scatter(RANDOM_X, RANDOM_Y)
# 横轴名称。
ax1.set_xlabel("x")
# 纵轴名称。
ax1.set_ylabel("y")

# 使用RANSAC算法估算模型
# 迭代最大次数，每次得到更好的估计会优化iters的数值
iters = 100000
# 数据和模型之间可接受的差值
sigma = 0.25
# 最好模型的参数估计和内点数目
best_a = 0
best_b = 0
pretotal = 0
# 希望的得到正确模型的概率
P = 0.99
for i in range(iters):
    # 随机在数据中红选出两个点去求解模型
    sample_index = random.sample(range(SIZE * 2),2)
    x_1 = RANDOM_X[sample_index[0]]
    x_2 = RANDOM_X[sample_index[1]]
    y_1 = RANDOM_Y[sample_index[0]]
    y_2 = RANDOM_Y[sample_index[1]]

    # y = ax + b 求解出a，b
    a = (y_2 - y_1) / (x_2 - x_1)
    b = y_1 - a * x_1

    # 算出内点数目
    total_inlier = 0
    for index in range(SIZE * 2):
        y_estimate = a * RANDOM_X[index] + b
        if abs(y_estimate - RANDOM_Y[index]) < sigma:
            total_inlier = total_inlier + 1

    # 判断当前的模型是否比之前估算的模型好
    if total_inlier > pretotal:
        iters = math.log(1 - P) / math.log(1 - pow(total_inlier / (SIZE * 2), 2))
        pretotal = total_inlier
        best_a = a
        best_b = b

    # 判断是否当前模型已经符合超过一半的点
    if total_inlier > SIZE:
        break

# 用我们得到的最佳估计画图
Y = best_a * RANDOM_X + best_b

# 直线图
ax1.plot(RANDOM_X, Y)
text = "best_a = " + str(best_a) + "\nbest_b = " + str(best_b)
plt.text(5,10, text,
         fontdict={'size': 8, 'color': 'r'})
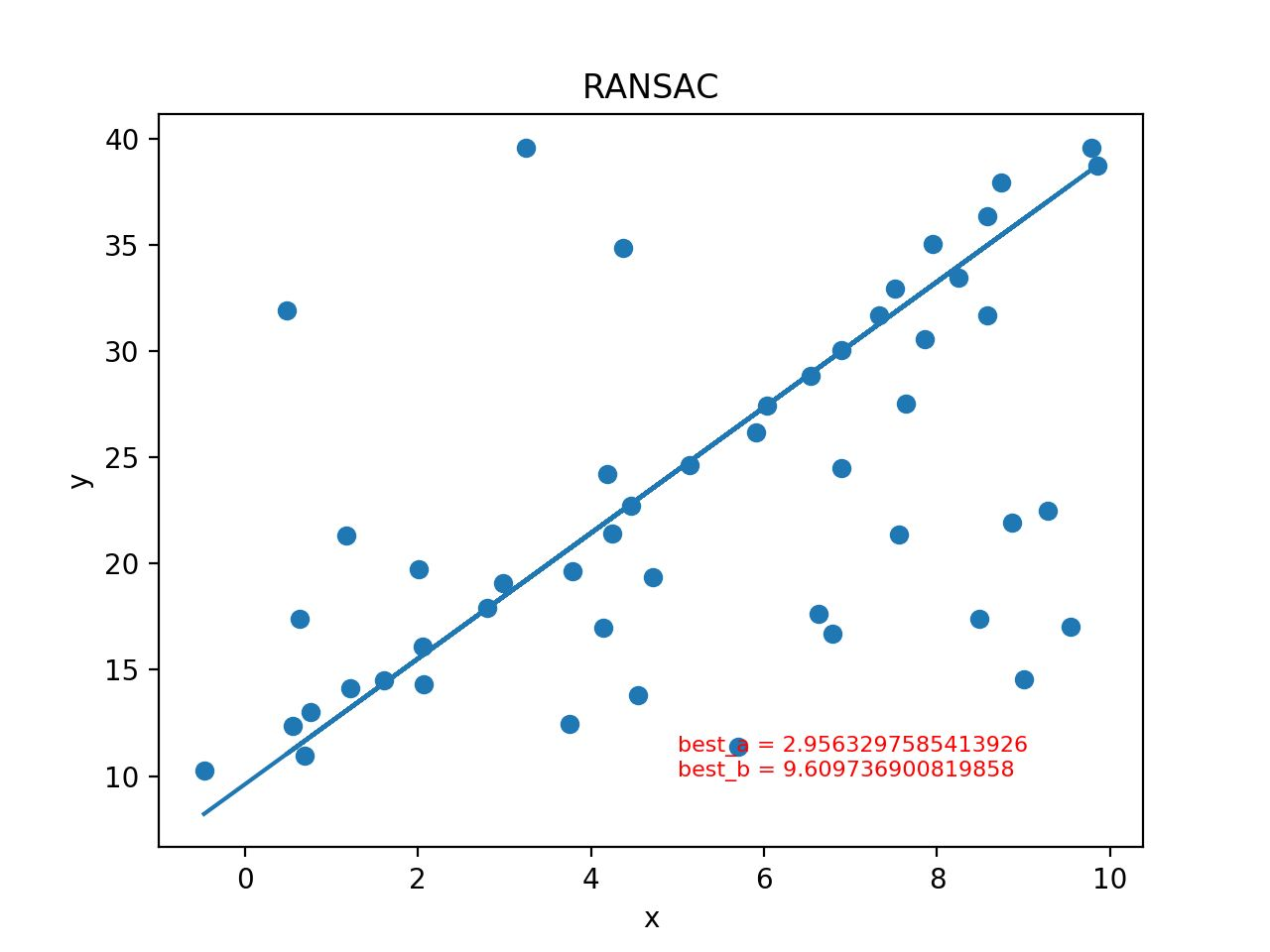
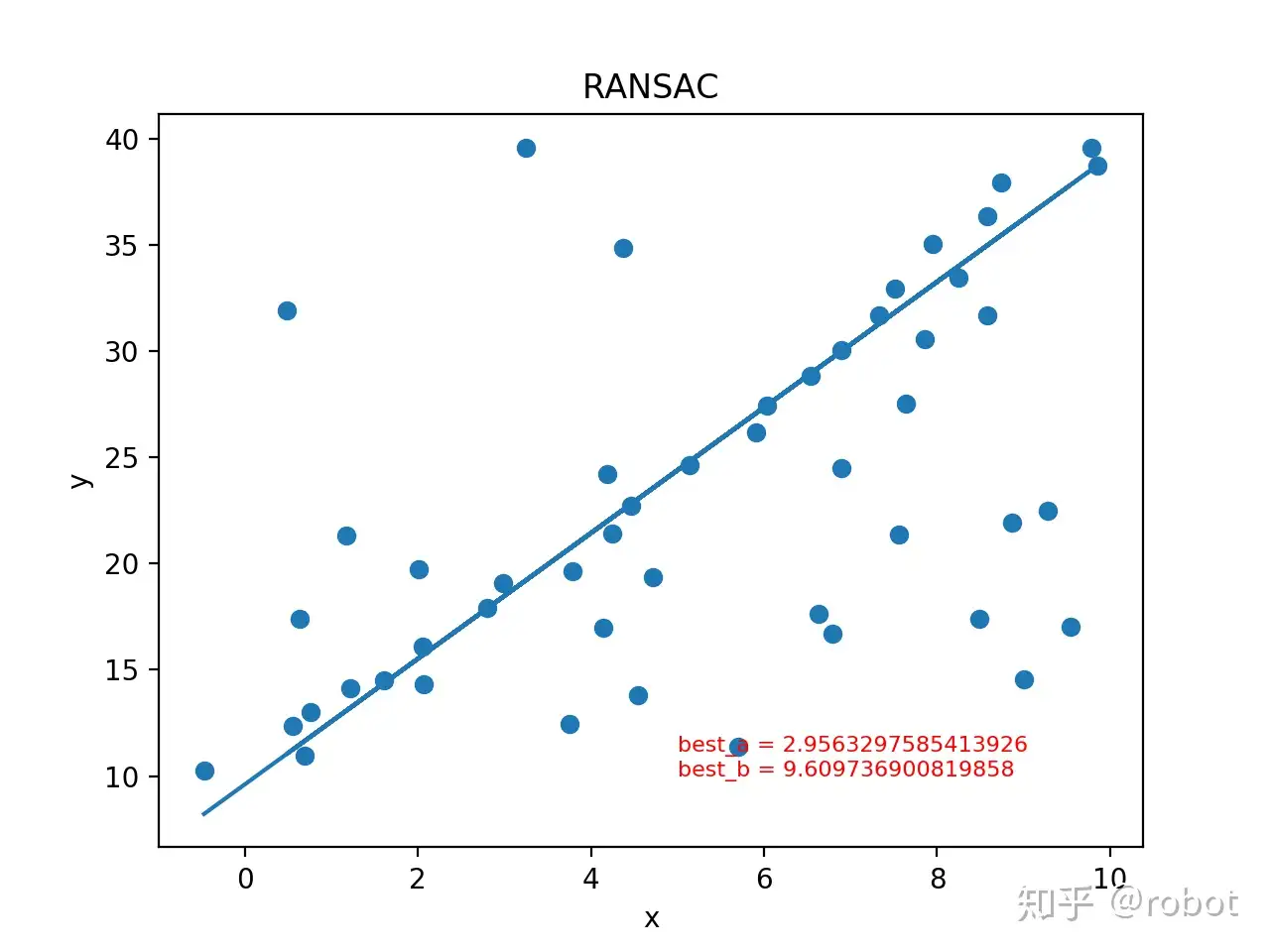
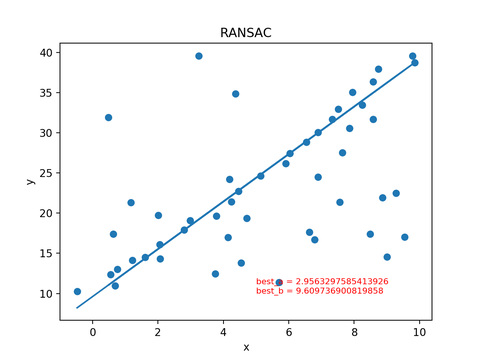
plt.show()

最后得到结果如下图：

RANSAC拟合曲线效果

RANSAC算法详解(附Python拟合曲线和平面)lixin97.com/2019/04/10/RANSAC/

编辑于 2019-04-13 14:50

posted on 2022-10-18 22:41 Sanny.Liu-CV&&ML 阅读(1086) 评论(0) 编辑收藏举报

刷新页面返回顶部

hansjorn