多目标跟踪，REID, JDE跟踪器解析

转载：https://zhuanlan.zhihu.com/p/133678626

转载：https://blog.csdn.net/kittyzc/article/details/107198055

转载：https://zhuanlan.zhihu.com/p/362715251

代码可以参考：https://github.com/xjsxujingsong/FairMOT_TensorRT_C 和 https://github.com/cooparation/JDE_Tracker

多目标跟踪原理解析

 

 

 

 与多目标跟踪（Multiple Object Tracking简称MOT）对应的是单目标跟踪（Single Object Tracking简称SOT），按照字面意思来理解，前者是对连续视频画面中多个目标进行跟踪，后者是对连续视频画面中单个目标进行跟踪。由于大部分应用场景都涉及到多个目标的跟踪，因此多目标跟踪也是目前大家主要研究内容，本文也主要介绍多目标跟踪。跟踪的本质是关联视频前后帧中的同一物体（目标），并赋予唯一TrackID

随着深度学习的兴起，目标检测的准确性越来越高，常见的yolo系列从V1到现在的V5（严格来讲V5不太算），mAP一个比一个高，因此基于深度学习的目标检测算法实际工程落地也越来越广泛，基于目标检测的跟踪我们称为Tracking By Detecting，目标检测算法的输出就是这种跟踪算法的输入，比如left, top,width,right坐标值。这种Tracking By Detecting的跟踪算法是大家讲得比较多、工业界用得也比较广的跟踪算法，我觉得主要还是归功于目标检测的成熟度越来越高。下面这张图描述了Tracking By Detecting的跟踪算法流程：

 

由上图可以看出，这种跟踪算法要求有一种检测算法配合起来使用，可想而知，前面检测算法的稳定性会严重影响后面跟踪算法的效果。图中实线圆形代表上一帧检测到的目标，虚线圆形代表当前帧检测到的目标，如何将前后帧目标正确关联起来就是这类跟踪算法需要解决的问题。目标跟踪是目标检测的后续补充，它是某些视频结构化应用中的必备环节，比如一些行为分析的应用系统中都需要先对检测出来的目标进行跟踪，然后再对跟踪到的轨迹进行分析。

目标关联

文章开头提到过，目标跟踪的本质是关联视频前后帧中的同一物体（目标），第T帧中有M个检测目标，第T+1帧中有N个检测目标，将前一帧中M个目标和后一帧中N个目标一一关联起来，并赋予唯一标识TrackID，这个过程就是Tracking By Detecting跟踪算法的宏观流程。

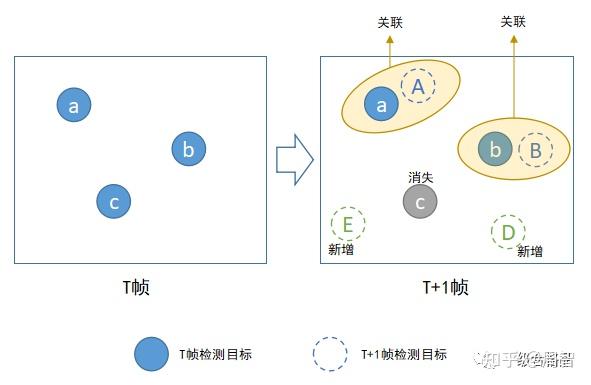
上图描述目标关联的具体流程，在实际目标关联过程中，我们需要考虑的有：

1、如何处理中途出现的新目标

2、如何处理中途消失的目标

3、正确目标关联

理想情况下，同一个物体（目标）在视频画面中从出现到消失，跟踪算法应该能赋予它唯一一个标识（TrackID），不管目标是否被遮挡、目标是否发生严重形变、是否和其他目标相距太近（相互干扰），只要这个目标被正确检测出来，跟踪算法都应该能够正确关联上。但实际上，物体遮挡是跟踪算法最难解决的难题之一，物体被频繁遮挡是TrackID变化的主要原因。原因很简单，物体被遮挡后（或其他原因），检测算法检测不到，跟踪算法无法连续关联到每帧的数据，等该物体再出现时，物体在画面中的位置、物体的外观形状与消失之前相比都发生了很大变化，而跟踪算法恰恰主要是根据物体的位置、外观来进行数据关联的。下面主要介绍目标跟踪中两种方式，一种容易实现、速度快，算法纯粹基于目标在画面中的位置来进行数据关联；另一种相对复杂，速度慢，算法需要提取前后帧中每个目标的图像特征（features），然后根据特征匹配去做数据关联。

 

基于坐标的目标关联

基于坐标（目标中心点+长宽）的目标关联是相对简单的一种目标跟踪方式，算法认为前后帧中挨得近的物体为同一个目标，因为物体移动是平滑缓慢的，具体可以通过IOU（交并比，前后两帧中目标检测方框的重叠程度）来计算，这种算法速度快、实现容易，在前面检测算法相对稳定的前提下，这种跟踪方式能够取得还不错的效果，由于速度快，这种方式一般可以用于对实时性（realtime）要求比较高的场合。缺点也很明显，因为它仅仅是以目标的坐标（检测算法的输出）为依据进行跟踪的，所以受检测算法影响非常大，如果检测算法不稳定，对于一个视频帧序列中的目标，检测算法经常漏检，那么通过这种方式去跟踪效果就非常差。另外如果场景比较复杂，目标比较密集，这种跟踪方式的效果也比不会太好，因为目标密集，相邻目标的坐标（left、top、width、height）重合度比较高，这给基于坐标的目标关联带来困难。

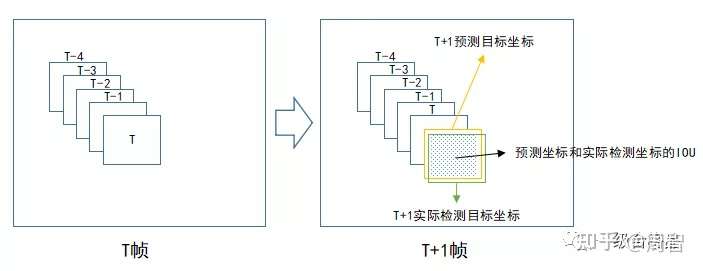
如上图，在T+1帧中，我们根据目标前面若干帧的坐标预测它在本帧中的坐标（预测坐标），然后再将该预测坐标与本帧实际检测的目标坐标进行数据关联。之所以需要先进行预测再关联，是因为为了减少关联过程的误差，常见预测算法可以使用卡尔曼滤波，根据目标前面若干坐标值预测下一坐标值，并且不断地进行自我修正，卡尔曼滤波算法网上有开源代码。IOU（交并比）是衡量两个矩形方框的重叠程度，IOU值越大代表矩形框重叠面积越大，它是目标检测中常见的概念。在这里，我们认为IOU越大，两个目标为同一物体的可能性越大。

 

基于特征的目标关联

纯粹基于坐标的目标跟踪算法有一定的局限性，单靠目标坐标去关联前后帧的同一目标在有些场合下效果比较差。在此基础上，有人提出结合目标外观特征匹配做目标关联，换句话说，在做目标关联的时候，除了依赖目标坐标外，还考虑目标的外观特征，道理很简单：

前后两帧中挨得近的物体且外观长得比较像的物体为同一目标。

这样的跟踪方式准确率更高，但是同时出现了一个问题：如何判断两个物体外观长得像？在计算机视觉中，有一个专门的研究领域叫Target Re-Identification（目标重识别），先通过对两个待比较目标进行特征编码（特征提取），然后再根据两个特征的相似度，来判断这两个目标是否为同一个物体，两个特征越相似代表两个目标为同一个物体的可能性越大。Target Re-Identification常用在图像搜索、轨迹生成（跨摄像机目标重识别）以及今天这里要说的目标跟踪。

熟悉深度学习的童鞋应该很清楚，神经网络的主要作用就是对原始输入数据进行特征编码，尤其在计算机视觉中，卷积神经网络主要用于图像的特征提取（Feature Extraction），从二维图像中提取高维特征，这些特征是对原始输入图像的一种抽象表示，因此训练神经网络的过程也可以称为Representation Learning。相同或者相似的输入图片，神经网络提取到的特征应该也是相同或者相似的。我们只要计算两个特征的相似度，就可以判断原始输入图像的相似性。

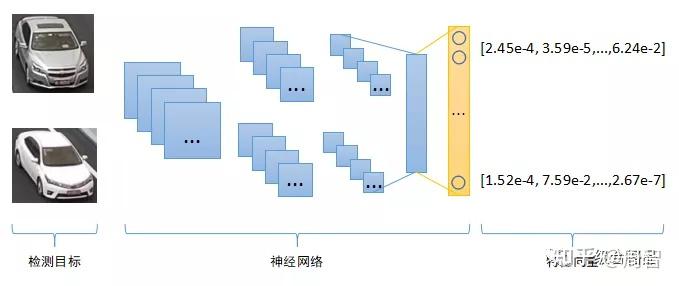
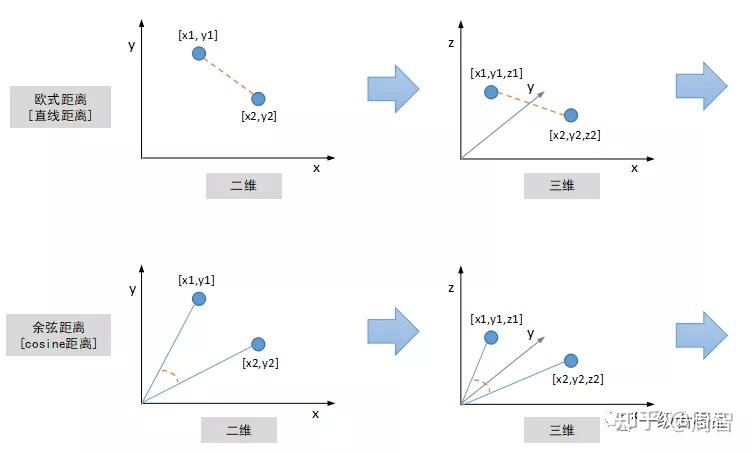
那么如何计算两个图像特征的相似度呢？图像特征的数学表示是一串数字，组合起来就是一个Vector向量，二维向量可以看成是平面坐标系中的点，三维向量可以看成立体空间中的点，依次类推，因此图像特征也被称作为“特征向量”。有很多度量标准来衡量两个特征向量的相似程度，最常见的是“欧式距离”，即计算两点之间的直线距离，二维三维空间中两点之间的直线距离我们都非常熟悉，更高维空间中两点距离计算原理跟二三维空间保持一致。另外除了“欧式距离”之外，还有一种常见距离度量标准叫“余弦距离”，计算两个向量（点到中心原点的射线）之间的夹角，夹角越小，代表两个向量越相似。

外观特征提取是一个耗时过程，因此对实时性要求比较高或者需要同时处理视频路数比较多的场合可能不太适合。但是这种基于外观特征的跟踪方式效果相对更好，对遮挡、目标密集等问题鲁棒性更好，因为目标遮挡再出现后，只要特征提取网络训练得够好，目标尺寸、角度变化对它的外观特征影响不大，因此关联准确性也更高。类似的，这个也适用于目标密集场景。外观特征提取需要定义一个合适的神经网络结构，采用相关素材去训练这个网络，网上有很多公开的Person-ReId数据集可以用来训练行人跟踪的特征提取网络，类似的，还有一些Vehicle-ReId数据集可以用来训练车辆跟踪的特征提取网络，关于这块的内容，也是一个值得深入研究的领域，由于本篇文章主要介绍目标跟踪，所以暂不展开讲述了

本文开头第一张图是基于坐标的跟踪方式效果图，基于外观特征中大部分时候目标ID都比较稳定，同样，人群密集场合中，同一目标ID发生改变的几率也小。实际上，同一目标ID是否发生变化是衡量跟踪算法好坏的一个重要指标，叫IDSwitch，同一目标ID变化次数越少，可以一定程度代表算法跟踪效果越好。

 

Deepsort 和FairMOT这种多目标跟踪的方法的后处理，都用到了这种JDEtracker的方式：

1. MOT主要步骤

在《DEEP LEARNING IN VIDEO MULTI-OBJECT TRACKING: A SURVEY》这篇基于深度学习的多目标跟踪的综述中，描述了MOT问题中四个主要步骤：

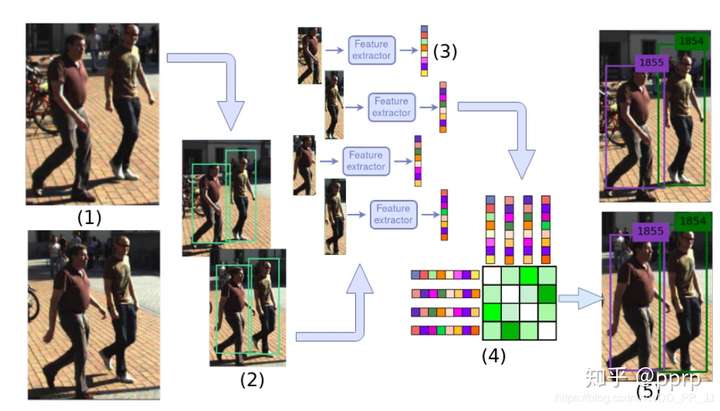
• 给定视频原始帧。
• 运行目标检测器如Faster R-CNN、YOLOv3、SSD等进行检测，获取目标检测框。
• 将所有目标框中对应的目标抠出来，进行特征提取（包括表观特征或者运动特征）。
• 进行相似度计算，计算前后两帧目标之间的匹配程度（前后属于同一个目标的之间的距离比较小，不同目标的距离比较大）
• 数据关联，为每个对象分配目标的ID。

以上就是四个核心步骤，其中核心是检测，SORT论文的摘要中提到，仅仅换一个更好的检测器，就可以将目标跟踪表现提升18.9%。

2. SORT

Deep SORT算法的前身是SORT, 全称是Simple Online and Realtime Tracking。简单介绍一下，SORT最大特点是基于Faster R-CNN的目标检测方法，并利用卡尔曼滤波算法+匈牙利算法，极大提高了多目标跟踪的速度，同时达到了SOTA的准确率。

这个算法确实是在实际应用中使用较为广泛的一个算法，核心就是两个算法：卡尔曼滤波和匈牙利算法。

卡尔曼滤波算法分为两个过程，预测和更新。该算法将目标的运动状态定义为8个正态分布的向量。

预测：当目标经过移动，通过上一帧的目标框和速度等参数，预测出当前帧的目标框位置和速度等参数。

更新：预测值和观测值，两个正态分布的状态进行线性加权，得到目前系统预测的状态。

**匈牙利算法：**解决的是一个分配问题，在MOT主要步骤中的计算相似度的，得到了前后两帧的相似度矩阵。匈牙利算法就是通过求解这个相似度矩阵，从而解决前后两帧真正匹配的目标。这部分sklearn库有对应的函数linear_assignment来进行求解。

SORT算法中是通过前后两帧IOU来构建相似度矩阵，所以SORT计算速度非常快。

下图是一张SORT核心算法流程图：

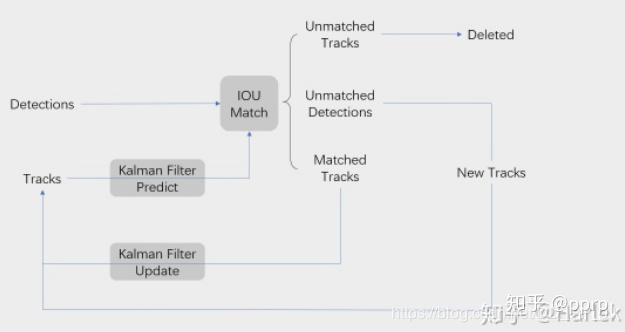
Detections是通过目标检测器得到的目标框，Tracks是一段轨迹。核心是匹配的过程与卡尔曼滤波的预测和更新过程。

流程如下：目标检测器得到目标框Detections，同时卡尔曼滤波器预测当前的帧的Tracks, 然后将Detections和Tracks进行IOU匹配，最终得到的结果分为：

• Unmatched Tracks，这部分被认为是失配，Detection和Track无法匹配，如果失配持续了次，该目标ID将从图片中删除。
• Unmatched Detections, 这部分说明没有任意一个Track能匹配Detection, 所以要为这个detection分配一个新的track。
• Matched Track，这部分说明得到了匹配。

卡尔曼滤波可以根据Tracks状态预测下一帧的目标框状态。

卡尔曼滤波更新是对观测值(匹配上的Track)和估计值更新所有track的状态。

3. Deep SORT

DeepSort中最大的特点是加入外观信息，借用了ReID领域模型来提取特征，减少了ID switch的次数。整体流程图如下：

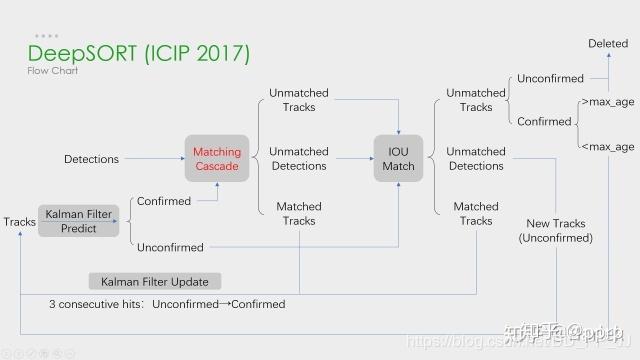
可以看出，Deep SORT算法在SORT算法的基础上增加了级联匹配(Matching Cascade)+新轨迹的确认(confirmed)。总体流程就是：

• 卡尔曼滤波器预测轨迹Tracks
• 使用匈牙利算法将预测得到的轨迹Tracks和当前帧中的detections进行匹配(级联匹配和IOU匹配)
• 卡尔曼滤波更新。

其中上图中的级联匹配展开如下：

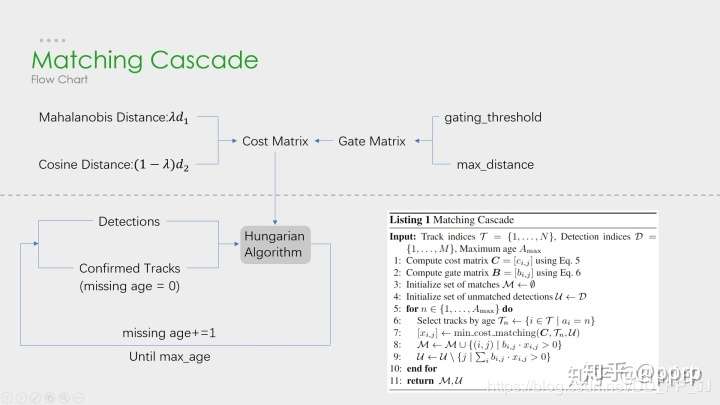
上图非常清晰地解释了如何进行级联匹配，上图由虚线划分为两部分：

上半部分中计算相似度矩阵的方法使用到了外观模型(ReID)和运动模型(马氏距离)来计算相似度，得到代价矩阵，另外一个则是门控矩阵，用于限制代价矩阵中过大的值。

下半部分中是是级联匹配的数据关联步骤，匹配过程是一个循环(max age个迭代，默认为70)，也就是从missing age=0到missing age=70的轨迹和Detections进行匹配，没有丢失过的轨迹优先匹配，丢失较为久远的就靠后匹配。通过这部分处理，可以重新将被遮挡目标找回，降低被遮挡然后再出现的目标发生的ID Switch次数。

将Detection和Track进行匹配，所以出现几种情况

1. Detection和Track匹配，也就是Matched Tracks。普通连续跟踪的目标都属于这种情况，前后两帧都有目标，能够匹配上。
2. Detection没有找到匹配的Track，也就是Unmatched Detections。图像中突然出现新的目标的时候，Detection无法在之前的Track找到匹配的目标。
3. Track没有找到匹配的Detection，也就是Unmatched Tracks。连续追踪的目标超出图像区域，Track无法与当前任意一个Detection匹配。
4. 以上没有涉及一种特殊的情况，就是两个目标遮挡的情况。刚刚被遮挡的目标的Track也无法匹配Detection，目标暂时从图像中消失。之后被遮挡目标再次出现的时候，应该尽量让被遮挡目标分配的ID不发生变动，减少ID Switch出现的次数，这就需要用到级联匹配了。

4. Deep SORT代码解析

论文中提供的代码是如下地址: https://github.com/nwojke/deep_sort

上图是Github库中有关Deep SORT的核心代码，不包括Faster R-CNN检测部分，所以主要将讲解这部分的几个文件，笔者也对其中核心代码进行了部分注释，地址在: https://github.com/pprp/deep_sort_yolov3_pytorch , 将其中的目标检测器换成了U版的yolov3, 将deep_sort文件中的核心进行了调用。

4.1 类图

下图是笔者总结的这几个类调用的类图(不是特别严谨，但是能大概展示各个模块的关系)：

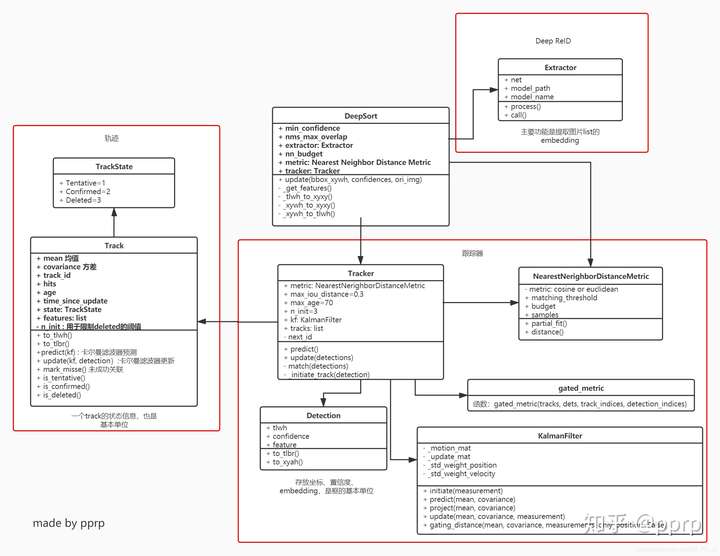
DeepSort是核心类，调用其他模块，大体上可以分为三个模块：

• ReID模块，用于提取表观特征，原论文中是生成了128维的embedding。
• Track模块，轨迹类，用于保存一个Track的状态信息，是一个基本单位。
• Tracker模块，Tracker模块掌握最核心的算法，卡尔曼滤波和匈牙利算法都是通过调用这个模块来完成的。

DeepSort类对外接口非常简单：

self.deepsort = DeepSort(args.deepsort_checkpoint)#实例化
outputs = self.deepsort.update(bbox_xcycwh, cls_conf, im)#通过接收目标检测结果进行更新

在外部调用的时候只需要以上两步即可，非常简单。

通过类图，对整体模块有了框架上理解，下面深入理解一下这些模块。

4.2 核心模块

Detection类

class Detection(object):
    """
    This class represents a bounding box detection in a single image.
 """
    def __init__(self, tlwh, confidence, feature):
        self.tlwh = np.asarray(tlwh, dtype=np.float)
        self.confidence = float(confidence)
        self.feature = np.asarray(feature, dtype=np.float32)
    def to_tlbr(self):
        """Convert bounding box to format `(min x, min y, max x, max y)`, i.e.,
        `(top left, bottom right)`.
        """
        ret = self.tlwh.copy()
        ret[2:] += ret[:2]
        return ret
    def to_xyah(self):
        """Convert bounding box to format `(center x, center y, aspect ratio,
        height)`, where the aspect ratio is `width / height`.
        """
        ret = self.tlwh.copy()
        ret[:2] += ret[2:] / 2
        ret[2] /= ret[3]
        return ret

Detection类用于保存通过目标检测器得到的一个检测框，包含top left坐标+框的宽和高，以及该bbox的置信度还有通过reid获取得到的对应的embedding。除此以外提供了不同bbox位置格式的转换方法：

• tlwh: 代表左上角坐标+宽高
• tlbr: 代表左上角坐标+右下角坐标
• xyah: 代表中心坐标+宽高比+高

Track类

class Track:
    # 一个轨迹的信息，包含(x,y,a,h) & v
    """
    A single target track with state space `(x, y, a, h)` and associated
    velocities, where `(x, y)` is the center of the bounding box, `a` is the
    aspect ratio and `h` is the height.
    """

    def __init__(self, mean, covariance, track_id, n_init, max_age,
                 feature=None):
        # max age是一个存活期限，默认为70帧,在
        self.mean = mean
        self.covariance = covariance
        self.track_id = track_id
        self.hits = 1 
        # hits和n_init进行比较
        # hits每次update的时候进行一次更新（只有match的时候才进行update）
        # hits代表匹配上了多少次，匹配次数超过n_init就会设置为confirmed状态
        self.age = 1 # 没有用到，和time_since_update功能重复
        self.time_since_update = 0
        # 每次调用predict函数的时候就会+1
        # 每次调用update函数的时候就会设置为0

        self.state = TrackState.Tentative
        self.features = []
        # 每个track对应多个features, 每次更新都将最新的feature添加到列表中
        if feature is not None:
            self.features.append(feature)

        self._n_init = n_init  # 如果连续n_init帧都没有出现失配，设置为deleted状态
        self._max_age = max_age  # 上限

Track类主要存储的是轨迹信息，mean和covariance是保存的框的位置和速度信息，track_id代表分配给这个轨迹的ID。state代表框的状态，有三种：

• Tentative: 不确定态，这种状态会在初始化一个Track的时候分配，并且只有在连续匹配上n_init帧才会转变为确定态。如果在处于不确定态的情况下没有匹配上任何detection，那将转变为删除态。
• Confirmed: 确定态，代表该Track确实处于匹配状态。如果当前Track属于确定态，但是失配连续达到max age次数的时候，就会被转变为删除态。
• Deleted: 删除态，说明该Track已经失效。

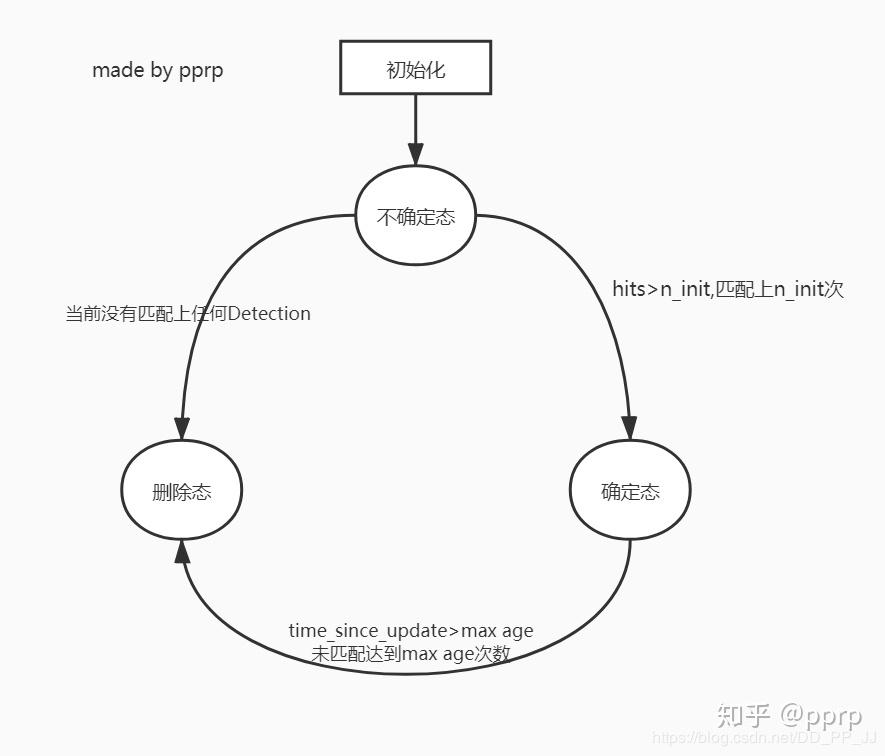
max_age代表一个Track存活期限，他需要和time_since_update变量进行比对。time_since_update是每次轨迹调用predict函数的时候就会+1，每次调用predict的时候就会重置为0，也就是说如果一个轨迹长时间没有update(没有匹配上)的时候，就会不断增加，直到time_since_update超过max age(默认70)，将这个Track从Tracker中的列表删除。

hits代表连续确认多少次，用在从不确定态转为确定态的时候。每次Track进行update的时候，hits就会+1, 如果hits>n_init(默认为3)，也就是连续三帧的该轨迹都得到了匹配，这时候才将不确定态转为确定态。

需要说明的是每个轨迹还有一个重要的变量，features列表，存储该轨迹在不同帧对应位置通过ReID提取到的特征。为何要保存这个列表，而不是将其更新为当前最新的特征呢？这是为了解决目标被遮挡后再次出现的问题，需要从以往帧对应的特征进行匹配。另外，如果特征过多会严重拖慢计算速度，所以有一个参数budget用来控制特征列表的长度，取最新的budget个features,将旧的删除掉。

ReID特征提取部分

ReID网络是独立于目标检测和跟踪器的模块，功能是提取对应bounding box中的feature,得到一个固定维度的embedding作为该bbox的代表，供计算相似度时使用。

class Extractor(object):
    def __init__(self, model_name, model_path, use_cuda=True):
        self.net = build_model(name=model_name,
                               num_classes=96)
        self.device = "cuda" if torch.cuda.is_available(
        ) and use_cuda else "cpu"
        state_dict = torch.load(model_path)['net_dict']
        self.net.load_state_dict(state_dict)
        print("Loading weights from {}... Done!".format(model_path))
        self.net.to(self.device)
        self.size = (128,128)
        self.norm = transforms.Compose([
            transforms.ToTensor(),
            transforms.Normalize([0.3568, 0.3141, 0.2781],
                                 [0.1752, 0.1857, 0.1879])
        ])

    def _preprocess(self, im_crops):
        """
        TODO:
            1. to float with scale from 0 to 1
            2. resize to (64, 128) as Market1501 dataset did
            3. concatenate to a numpy array
            3. to torch Tensor
            4. normalize
        """
        def _resize(im, size):
            return cv2.resize(im.astype(np.float32) / 255., size)

        im_batch = torch.cat([
            self.norm(_resize(im, self.size)).unsqueeze(0) for im in im_crops
        ],dim=0).float()
        return im_batch

    def __call__(self, im_crops):
        im_batch = self._preprocess(im_crops)
        with torch.no_grad():
            im_batch = im_batch.to(self.device)
            features = self.net(im_batch)
        return features.cpu().numpy()

模型训练是按照传统ReID的方法进行，使用Extractor类的时候输入为一个list的图片，得到图片对应的特征。

NearestNeighborDistanceMetric类

这个类中用到了两个计算距离的函数：

1. 计算欧氏距离

def _pdist(a, b):
    # 用于计算成对的平方距离
    # a NxM 代表N个对象，每个对象有M个数值作为embedding进行比较
    # b LxM 代表L个对象，每个对象有M个数值作为embedding进行比较
    # 返回的是NxL的矩阵，比如dist[i][j]代表a[i]和b[j]之间的平方和距离
    # 实现见：https://blog.csdn.net/frankzd/article/details/80251042
    a, b = np.asarray(a), np.asarray(b)  # 拷贝一份数据
    if len(a) == 0 or len(b) == 0:
        return np.zeros((len(a), len(b)))
    a2, b2 = np.square(a).sum(axis=1), np.square(
        b).sum(axis=1)  # 求每个embedding的平方和
    # sum(N) + sum(L) -2 x [NxM]x[MxL] = [NxL]
    r2 = -2. * np.dot(a, b.T) + a2[:, None] + b2[None, :]
    r2 = np.clip(r2, 0., float(np.inf))
    return r2

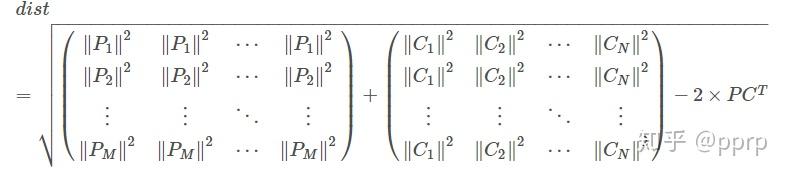
1. 计算余弦距离

def _cosine_distance(a, b, data_is_normalized=False):
    # a和b之间的余弦距离
    # a : [NxM] b : [LxM]
    # 余弦距离 = 1 - 余弦相似度
    # https://blog.csdn.net/u013749540/article/details/51813922
    if not data_is_normalized:
        # 需要将余弦相似度转化成类似欧氏距离的余弦距离。
        a = np.asarray(a) / np.linalg.norm(a, axis=1, keepdims=True)
        #  np.linalg.norm 操作是求向量的范式，默认是L2范式，等同于求向量的欧式距离。
        b = np.asarray(b) / np.linalg.norm(b, axis=1, keepdims=True)
    return 1. - np.dot(a, b.T)

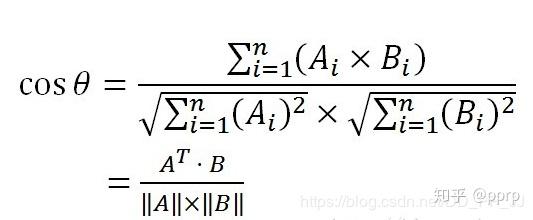
以上代码对应公式，注意余弦距离=1-余弦相似度。

最近邻距离度量类

class NearestNeighborDistanceMetric(object):
    # 对于每个目标，返回一个最近的距离
    def __init__(self, metric, matching_threshold, budget=None):
        # 默认matching_threshold = 0.2 budge = 100
        if metric == "euclidean":
            # 使用最近邻欧氏距离
            self._metric = _nn_euclidean_distance
        elif metric == "cosine":
            # 使用最近邻余弦距离
            self._metric = _nn_cosine_distance
        else:
            raise ValueError("Invalid metric; must be either 'euclidean' or 'cosine'")

        self.matching_threshold = matching_threshold
        # 在级联匹配的函数中调用
        self.budget = budget
        # budge 预算，控制feature的多少
        self.samples = {}
        # samples是一个字典{id->feature list}

    def partial_fit(self, features, targets, active_targets):
        # 作用：部分拟合，用新的数据更新测量距离
        # 调用：在特征集更新模块部分调用，tracker.update()中
        for feature, target in zip(features, targets):
            self.samples.setdefault(target, []).append(feature)
            # 对应目标下添加新的feature，更新feature集合
            # 目标id  :  feature list
            if self.budget is not None:
                self.samples[target] = self.samples[target][-self.budget:]
            # 设置预算，每个类最多多少个目标，超过直接忽略

        # 筛选激活的目标
        self.samples = {k: self.samples[k] for k in active_targets}

    def distance(self, features, targets):
        # 作用：比较feature和targets之间的距离，返回一个代价矩阵
        # 调用：在匹配阶段，将distance封装为gated_metric,
        #       进行外观信息(reid得到的深度特征)+
        #       运动信息(马氏距离用于度量两个分布相似程度)
        cost_matrix = np.zeros((len(targets), len(features)))
        for i, target in enumerate(targets):
            cost_matrix[i, :] = self._metric(self.samples[target], features)
        return cost_matrix

Tracker类

Tracker类是最核心的类，Tracker中保存了所有的轨迹信息，负责初始化第一帧的轨迹、卡尔曼滤波的预测和更新、负责级联匹配、IOU匹配等等核心工作。

class Tracker:
    # 是一个多目标tracker，保存了很多个track轨迹
    # 负责调用卡尔曼滤波来预测track的新状态+进行匹配工作+初始化第一帧
    # Tracker调用update或predict的时候，其中的每个track也会各自调用自己的update或predict
    """
    This is the multi-target tracker.
    """

    def __init__(self, metric, max_iou_distance=0.7, max_age=70, n_init=3):
        # 调用的时候，后边的参数全部是默认的
        self.metric = metric 
        # metric是一个类，用于计算距离(余弦距离或马氏距离)
        self.max_iou_distance = max_iou_distance
        # 最大iou，iou匹配的时候使用
        self.max_age = max_age
        # 直接指定级联匹配的cascade_depth参数
        self.n_init = n_init
        # n_init代表需要n_init次数的update才会将track状态设置为confirmed

        self.kf = kalman_filter.KalmanFilter()# 卡尔曼滤波器
        self.tracks = [] # 保存一系列轨迹
        self._next_id = 1 # 下一个分配的轨迹id
 def predict(self):
        # 遍历每个track都进行一次预测
        """Propagate track state distributions one time step forward.

        This function should be called once every time step, before `update`.
        """
        for track in self.tracks:
            track.predict(self.kf)

然后来看最核心的update函数和match函数，可以对照下面的流程图一起看：

update函数

def update(self, detections):
    # 进行测量的更新和轨迹管理
    """Perform measurement update and track management.

    Parameters
    ----------
    detections : List[deep_sort.detection.Detection]
        A list of detections at the current time step.

    """
    # Run matching cascade.
    matches, unmatched_tracks, unmatched_detections = \
        self._match(detections)

    # Update track set.
    # 1. 针对匹配上的结果
    for track_idx, detection_idx in matches:
        # track更新对应的detection
        self.tracks[track_idx].update(self.kf, detections[detection_idx])

    # 2. 针对未匹配的tracker,调用mark_missed标记
    # track失配，若待定则删除，若update时间很久也删除
    # max age是一个存活期限，默认为70帧
    for track_idx in unmatched_tracks:
        self.tracks[track_idx].mark_missed()

    # 3. 针对未匹配的detection， detection失配，进行初始化
    for detection_idx in unmatched_detections:
        self._initiate_track(detections[detection_idx])

    # 得到最新的tracks列表，保存的是标记为confirmed和Tentative的track
    self.tracks = [t for t in self.tracks if not t.is_deleted()]

    # Update distance metric.
    active_targets = [t.track_id for t in self.tracks if t.is_confirmed()]
    # 获取所有confirmed状态的track id
    features, targets = [], []
    for track in self.tracks:
        if not track.is_confirmed():
            continue
        features += track.features  # 将tracks列表拼接到features列表
        # 获取每个feature对应的track id
        targets += [track.track_id for _ in track.features]
        track.features = []

    # 距离度量中的 特征集更新
    self.metric.partial_fit(np.asarray(features), np.asarray(targets),
                            active_targets)

match函数：

def _match(self, detections):
    # 主要功能是进行匹配，找到匹配的，未匹配的部分
    def gated_metric(tracks, dets, track_indices, detection_indices):
        # 功能： 用于计算track和detection之间的距离，代价函数
        #        需要使用在KM算法之前
        # 调用：
        # cost_matrix = distance_metric(tracks, detections,
        #                  track_indices, detection_indices)
        features = np.array([dets[i].feature for i in detection_indices])
        targets = np.array([tracks[i].track_id for i in track_indices])

        # 1. 通过最近邻计算出代价矩阵 cosine distance
        cost_matrix = self.metric.distance(features, targets)
        # 2. 计算马氏距离,得到新的状态矩阵
        cost_matrix = linear_assignment.gate_cost_matrix(
            self.kf, cost_matrix, tracks, dets, track_indices,
            detection_indices)
        return cost_matrix

    # Split track set into confirmed and unconfirmed tracks.
    # 划分不同轨迹的状态
    confirmed_tracks = [
        i for i, t in enumerate(self.tracks) if t.is_confirmed()
    ]
    unconfirmed_tracks = [
        i for i, t in enumerate(self.tracks) if not t.is_confirmed()
    ]

    # 进行级联匹配，得到匹配的track、不匹配的track、不匹配的detection
    '''
    !!!!!!!!!!!
    级联匹配
    !!!!!!!!!!!
    '''
    # gated_metric->cosine distance
    # 仅仅对确定态的轨迹进行级联匹配
    matches_a, unmatched_tracks_a, unmatched_detections = \
        linear_assignment.matching_cascade(
            gated_metric,
            self.metric.matching_threshold,
            self.max_age,
            self.tracks,
            detections,
            confirmed_tracks)

    # 将所有状态为未确定态的轨迹和刚刚没有匹配上的轨迹组合为iou_track_candidates，
    # 进行IoU的匹配
    iou_track_candidates = unconfirmed_tracks + [
        k for k in unmatched_tracks_a
        if self.tracks[k].time_since_update == 1  # 刚刚没有匹配上
    ]
    # 未匹配
    unmatched_tracks_a = [
        k for k in unmatched_tracks_a
        if self.tracks[k].time_since_update != 1  # 已经很久没有匹配上
    ]

    '''
    !!!!!!!!!!!
    IOU 匹配
    对级联匹配中还没有匹配成功的目标再进行IoU匹配
    !!!!!!!!!!!
    '''
    # 虽然和级联匹配中使用的都是min_cost_matching作为核心，
    # 这里使用的metric是iou cost和以上不同
    matches_b, unmatched_tracks_b, unmatched_detections = \
        linear_assignment.min_cost_matching(
            iou_matching.iou_cost,
            self.max_iou_distance,
            self.tracks,
            detections,
            iou_track_candidates,
            unmatched_detections)

    matches = matches_a + matches_b  # 组合两部分match得到的结果

    unmatched_tracks = list(set(unmatched_tracks_a + unmatched_tracks_b))
    return matches, unmatched_tracks, unmatched_detections

以上两部分结合注释和以下流程图可以更容易理解。

级联匹配

下边是论文中给出的级联匹配的伪代码：

以下代码是伪代码对应的实现

# 1. 分配track_indices和detection_indices
if track_indices is None:
    track_indices = list(range(len(tracks)))

if detection_indices is None:
    detection_indices = list(range(len(detections)))

unmatched_detections = detection_indices

matches = []
# cascade depth = max age 默认为70
for level in range(cascade_depth):
    if len(unmatched_detections) == 0:  # No detections left
        break

    track_indices_l = [
        k for k in track_indices
        if tracks[k].time_since_update == 1 + level
    ]
    if len(track_indices_l) == 0:  # Nothing to match at this level
        continue

    # 2. 级联匹配核心内容就是这个函数
    matches_l, _, unmatched_detections = \
        min_cost_matching(  # max_distance=0.2
            distance_metric, max_distance, tracks, detections,
            track_indices_l, unmatched_detections)
    matches += matches_l
unmatched_tracks = list(set(track_indices) - set(k for k, _ in matches))

门控矩阵

门控矩阵的作用就是通过计算卡尔曼滤波的状态分布和测量值之间的距离对代价矩阵进行限制。

代价矩阵中的距离是Track和Detection之间的表观相似度，假如一个轨迹要去匹配两个表观特征非常相似的Detection，这样就很容易出错，但是这个时候分别让两个Detection计算与这个轨迹的马氏距离，并使用一个阈值gating_threshold进行限制，所以就可以将马氏距离较远的那个Detection区分开，可以降低错误的匹配。

def gate_cost_matrix(
        kf, cost_matrix, tracks, detections, track_indices, detection_indices,
        gated_cost=INFTY_COST, only_position=False):
    # 根据通过卡尔曼滤波获得的状态分布，使成本矩阵中的不可行条目无效。
    gating_dim = 2 if only_position else 4
    gating_threshold = kalman_filter.chi2inv95[gating_dim]  # 9.4877

    measurements = np.asarray([detections[i].to_xyah()
                               for i in detection_indices])
    for row, track_idx in enumerate(track_indices):
        track = tracks[track_idx]
        gating_distance = kf.gating_distance(
            track.mean, track.covariance, measurements, only_position)
        cost_matrix[row, gating_distance >
                    gating_threshold] = gated_cost  # 设置为inf
    return cost_matrix

卡尔曼滤波器

在Deep SORT中，需要估计Track的以下状态：

• 均值：用8维向量（x, y, a, h, vx, vy, va, vh）表示。(x,y)是框的中心坐标，宽高比是a, 高度h以及对应的速度，所有的速度都将初始化为0。
• 协方差：表示目标位置信息的不确定程度，用8x8的对角矩阵来表示，矩阵对应的值越大，代表不确定程度越高。

下图代表卡尔曼滤波器主要过程：

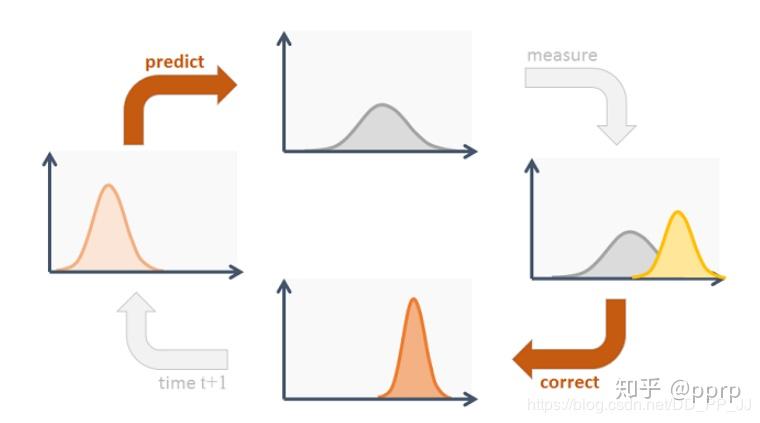
1. 卡尔曼滤波首先根据当前帧(time=t)的状态进行预测，得到预测下一帧的状态(time=t+1)
2. 得到测量结果，在Deep SORT中对应的测量就是Detection，即目标检测器提供的检测框。
3. 将预测结果和测量结果进行更新。

下面这部分主要参考： https://zhuanlan.zhihu.com/p/90835266

如果对卡尔曼滤波算法有较为深入的了解，可以结合卡尔曼滤波算法和代码进行理解。

预测分两个公式：

第一个公式：

其中F是状态转移矩阵，如下图：

第二个公式：

P是当前帧(time=t)的协方差，Q是卡尔曼滤波器的运动估计误差，代表不确定程度。

def predict(self, mean, covariance):
    # 相当于得到t时刻估计值
    # Q 预测过程中噪声协方差
    std_pos = [
        self._std_weight_position * mean[3],
        self._std_weight_position * mean[3],
        1e-2,
        self._std_weight_position * mean[3]]

    std_vel = [
        self._std_weight_velocity * mean[3],
        self._std_weight_velocity * mean[3],
        1e-5,
        self._std_weight_velocity * mean[3]]

    # np.r_ 按列连接两个矩阵
    # 初始化噪声矩阵Q
    motion_cov = np.diag(np.square(np.r_[std_pos, std_vel]))

    # x' = Fx
    mean = np.dot(self._motion_mat, mean)

    # P' = FPF^T+Q
    covariance = np.linalg.multi_dot((
        self._motion_mat, covariance, self._motion_mat.T)) + motion_cov

    return mean, covariance

更新的公式

def project(self, mean, covariance):
    # R 测量过程中噪声的协方差
    std = [
        self._std_weight_position * mean[3],
        self._std_weight_position * mean[3],
        1e-1,
        self._std_weight_position * mean[3]]

    # 初始化噪声矩阵R
    innovation_cov = np.diag(np.square(std))

    # 将均值向量映射到检测空间，即Hx'
    mean = np.dot(self._update_mat, mean)

    # 将协方差矩阵映射到检测空间，即HP'H^T
    covariance = np.linalg.multi_dot((
        self._update_mat, covariance, self._update_mat.T))

    return mean, covariance + innovation_cov

def update(self, mean, covariance, measurement):
    # 通过估计值和观测值估计最新结果

    # 将均值和协方差映射到检测空间，得到 Hx' 和 S
    projected_mean, projected_cov = self.project(mean, covariance)

    # 矩阵分解
    chol_factor, lower = scipy.linalg.cho_factor(
        projected_cov, lower=True, check_finite=False)

    # 计算卡尔曼增益K
    kalman_gain = scipy.linalg.cho_solve(
        (chol_factor, lower), np.dot(covariance, self._update_mat.T).T,
        check_finite=False).T

    # z - Hx'
    innovation = measurement - projected_mean

    # x = x' + Ky
    new_mean = mean + np.dot(innovation, kalman_gain.T)

    # P = (I - KH)P'
    new_covariance = covariance - np.linalg.multi_dot((
        kalman_gain, projected_cov, kalman_gain.T))
    return new_mean, new_covariance

这个公式中，z是Detection的mean，不包含变化值，状态为[cx,cy,a,h]。H是测量矩阵，将Track的均值向量映射到检测空间。计算的y是Detection和Track的均值误差。

R是目标检测器的噪声矩阵，是一个4x4的对角矩阵。 对角线上的值分别为中心点两个坐标以及宽高的噪声。

计算的是卡尔曼增益，是作用于衡量估计误差的权重。

更新后的均值向量x。

更新后的协方差矩阵。

卡尔曼滤波笔者理解也不是很深入，没有推导过公式，对这部分感兴趣的推荐几个博客：

1. 卡尔曼滤波+python写的demo: https://zhuanlan.zhihu.com/p/113685503?utm_source=wechat_session&utm_medium=social&utm_oi=801414067897135104
2. 详解+推导： https://blog.csdn.net/honyniu/article/details/88697520

参考

https://arxiv.org/abs/1703.07402

https://github.com/pprp/deep_sort_yolov3_pytorch

https://www.cnblogs.com/yanwei-li/p/8643446.html

https://zhuanlan.zhihu.com/p/97449724

https://zhuanlan.zhihu.com/p/80764724

https://zhuanlan.zhihu.com/p/90835266

https://zhuanlan.zhihu.com/p/11