损失函数 (Loss Function)解释
转载:https://mp.weixin.qq.com/s/Xbi5iOh3xoBIK5kVmqbKYA
https://baijiahao.baidu.com/s?id=1611951775526158371&wfr=spider&for=pc
https://zhuanlan.zhihu.com/p/75074145
- 各个损失函数的导数
计算值:
真实值:
pytorch很多的loss 函数都有size_average和reduce两个布尔类型的参数,需要解释一下。因为一般损失函数都是直接计算 batch 的数据,因此返回的 loss 结果都是维度为(batch_size, ) 的向量。
- 如果 reduce = False,那么 size_average 参数失效,直接返回向量形式的 loss;
- 如果 reduce = True,那么 loss 返回的是标量
- 如果 size_average = True,返回 loss.mean();
- 如果 size_average = True,返回 loss.sum();
若把这两个参数设置成 False,这样子比较好理解原始的损失函数定义。
无论在机器学习还是深度领域中,损失函数都是一个非常重要的知识点。损失函数(Loss Function)是用来估量模型的预测值 f(x) 与真实值 y 的不一致程度。我们的目标就是最小化损失函数,让 f(x) 与 y 尽量接近。通常可以使用梯度下降算法寻找函数最小值。
关于梯度下降最直白的解释可以看我的这篇文章:
损失函数有许多不同的类型,没有哪种损失函数适合所有的问题,需根据具体模型和问题进行选择。一般来说,损失函数大致可以分成两类:回归(Regression)和分类(Classification)。今天,红色石头将要总结回归问题中常用的 3 种损失函数,希望对你有所帮助。
回归模型中的三种损失函数包括:均方误差(Mean Square Error)、平均绝对误差(Mean Absolute Error,MAE)、Huber Loss。
- 均方误差(Mean Square Error,MSE)
均方误差指的就是模型预测值 f(x) 与样本真实值 y 之间距离平方的平均值。其公式如下所示:
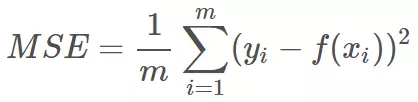
其中,yi 和 f(xi) 分别表示第 i 个样本的真实值和预测值,m 为样本个数。
为了简化讨论,忽略下标 i,m = 1,以 y-f(x) 为横坐标,MSE 为纵坐标,绘制其损失函数的图形:

MSE 曲线的特点是光滑连续、可导,便于使用梯度下降算法,是比较常用的一种损失函数。而且,MSE 随着误差的减小,梯度也在减小,这有利于函数的收敛,即使固定学习因子,函数也能较快取得最小值。
平方误差有个特性,就是当 yi 与 f(xi) 的差值大于 1 时,会增大其误差;当 yi 与 f(xi) 的差值小于 1 时,会减小其误差。这是由平方的特性决定的。也就是说, MSE 会对误差较大(>1)的情况给予更大的惩罚,对误差较小(<1)的情况给予更小的惩罚。从训练的角度来看,模型会更加偏向于惩罚较大的点,赋予其更大的权重。
如果样本中存在离群点,MSE 会给离群点赋予更高的权重,但是却是以牺牲其他正常数据点的预测效果为代价,这最终会降低模型的整体性能。我们来看一下使用 MSE 解决含有离群点的回归模型。
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1, 20, 40)
y = x + [np.random.choice(4) for _ in range(40)]
y[-5:] -= 8
X = np.vstack((np.ones_like(x),x)) # 引入常数项 1
m = X.shape[1]
# 参数初始化
W = np.zeros((1,2))
# 迭代训练
num_iter = 20
lr = 0.01
J = []
for i in range(num_iter):
y_pred = W.dot(X)
loss = 1/(2*m) * np.sum((y-y_pred)**2)
J.append(loss)
W = W + lr * 1/m * (y-y_pred).dot(X.T)
# 作图
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2])
plt.show()拟合结果如下图所示:
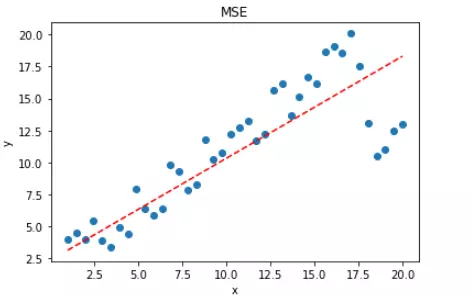
可见,使用 MSE 损失函数,受离群点的影响较大,虽然样本中只有 5 个离群点,但是拟合的直线还是比较偏向于离群点。这往往是我们不希望看到的。
- 平均绝对误差(Mean Absolute Error,MAE)
平均绝对误差指的就是模型预测值 f(x) 与样本真实值 y 之间距离的平均值。其公式如下所示:
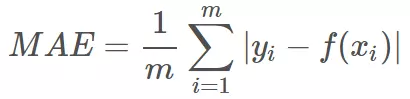
为了简化讨论,忽略下标 i,m = 1,以 y-f(x) 为横坐标,MAE 为纵坐标,绘制其损失函数的图形:
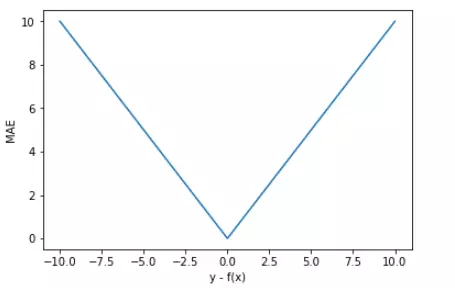
直观上来看,MAE 的曲线呈 V 字型,连续但在 y-f(x)=0 处不可导,计算机求解导数比较困难。而且 MAE 大部分情况下梯度都是相等的,这意味着即使对于小的损失值,其梯度也是大的。这不利于函数的收敛和模型的学习。
值得一提的是,MAE 相比 MSE 有个优点就是 MAE 对离群点不那么敏感,更有包容性。因为 MAE 计算的是误差 y-f(x) 的绝对值,无论是 y-f(x)>1 还是 y-f(x)<1,没有平方项的作用,惩罚力度都是一样的,所占权重一样。针对 MSE 中的例子,我们来使用 MAE 进行求解,看下拟合直线有什么不同。
X = np.vstack((np.ones_like(x),x)) # 引入常数项 1
m = X.shape[1]
# 参数初始化
W = np.zeros((1,2))
# 迭代训练
num_iter = 20
lr = 0.01
J = []
for i in range(num_iter):
y_pred = W.dot(X)
loss = 1/m * np.sum(np.abs(y-y_pred))
J.append(loss)
mask = (y-y_pred).copy()
mask[y-y_pred > 0] = 1
mask[mask <= 0] = -1
W = W + lr * 1/m * mask.dot(X.T)
# 作图
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2],'r--')
plt.xlabel('x')
plt.ylabel('y')
plt.title('MAE')
plt.show()注意上述代码中对 MAE 计算梯度的部分。
拟合结果如下图所示:
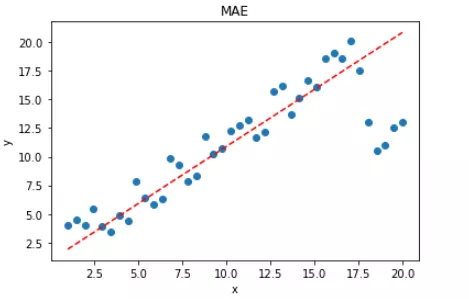
显然,使用 MAE 损失函数,受离群点的影响较小,拟合直线能够较好地表征正常数据的分布情况。这一点,MAE 要优于 MSE。二者的对比图如下:

选择 MSE 还是 MAE 呢?
实际应用中,我们应该选择 MSE 还是 MAE 呢?从计算机求解梯度的复杂度来说,MSE 要优于 MAE,而且梯度也是动态变化的,能较快准确达到收敛。但是从离群点角度来看,如果离群点是实际数据或重要数据,而且是应该被检测到的异常值,那么我们应该使用MSE。另一方面,离群点仅仅代表数据损坏或者错误采样,无须给予过多关注,那么我们应该选择MAE作为损失。
- Huber Loss
既然 MSE 和 MAE 各有优点和缺点,那么有没有一种激活函数能同时消除二者的缺点,集合二者的优点呢?答案是有的。Huber Loss 就具备这样的优点,其公式如下:
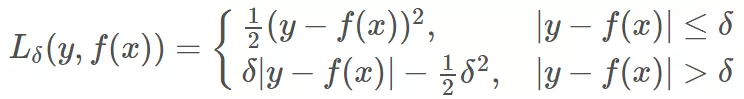
Huber Loss 是对二者的综合,包含了一个超参数 δ。δ 值的大小决定了 Huber Loss 对 MSE 和 MAE 的侧重性,当 |y−f(x)| ≤ δ 时,变为 MSE;当 |y−f(x)| > δ 时,则变成类似于 MAE,因此 Huber Loss 同时具备了 MSE 和 MAE 的优点,减小了对离群点的敏感度问题,实现了处处可导的功能。
通常来说,超参数 δ 可以通过交叉验证选取最佳值。下面,分别取 δ = 0.1、δ = 10,绘制相应的 Huber Loss,如下图所示:
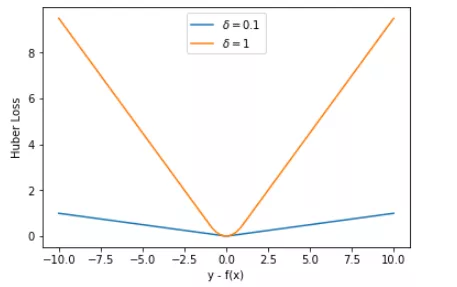
Huber Loss 在 |y−f(x)| > δ 时,梯度一直近似为 δ,能够保证模型以一个较快的速度更新参数。当 |y−f(x)| ≤ δ 时,梯度逐渐减小,能够保证模型更精确地得到全局最优值。因此,Huber Loss 同时具备了前两种损失函数的优点。
下面,我们用 Huber Loss 来解决同样的例子。
X = np.vstack((np.ones_like(x),x)) # 引入常数项 1
m = X.shape[1]
# 参数初始化
W = np.zeros((1,2))
# 迭代训练
num_iter = 20
lr = 0.01
delta = 2
J = []
for i in range(num_iter):
y_pred = W.dot(X)
loss = 1/m * np.sum(np.abs(y-y_pred))
J.append(loss)
mask = (y-y_pred).copy()
mask[y-y_pred > delta] = delta
mask[mask < -delta] = -delta
W = W + lr * 1/m * mask.dot(X.T)
# 作图
y1 = W[0,0] + W[0,1]*1
y2 = W[0,0] + W[0,1]*20
plt.scatter(x, y)
plt.plot([1,20],[y1,y2],'r--')
plt.xlabel('x')
plt.ylabel('y')
plt.title('MAE')
plt.show()注意上述代码中对 Huber Loss 计算梯度的部分。
拟合结果如下图所示:
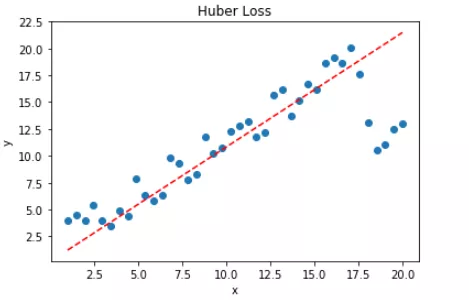
可见,使用 Huber Loss 作为激活函数,对离群点仍然有很好的抗干扰性,这一点比 MSE 强。另外,我们把这三种损失函数对应的 Loss 随着迭代次数变化的趋势绘制出来:
MSE:
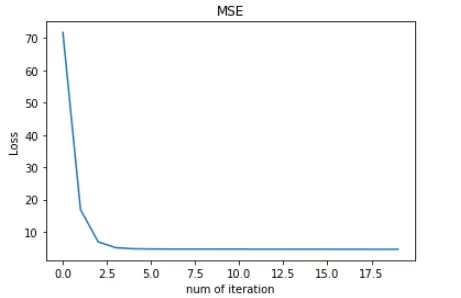
MAE:

Huber Loss:
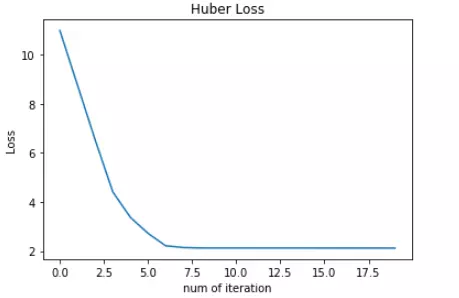
对比发现,MSE 的 Loss 下降得最快,MAE 的 Loss 下降得最慢,Huber Loss 下降速度介于 MSE 和 MAE 之间。也就是说,Huber Loss 弥补了此例中 MAE 的 Loss 下降速度慢的问题,使得优化速度接近 MSE。
最后,我们把以上介绍的回归问题中的三种损失函数全部绘制在一张图上。

好了,以上就是红色石头对回归问题 3 种常用的损失函数包括:MSE、MAE、Huber Loss 的简单介绍和详细对比。这些简单的知识点你是否已经完全掌握了呢?
- BCELoss、BCEWithLogitsLoss
2、BCELoss(二分类用的交叉熵损失函数)
用的时候需要在该层前面加上Sigmoid函数
因为只有正例和反例,且两者的概率和为 1,那么只需要预测一个概率就好了,可以简化成:
loss_fn = torch.nn.BCELoss(reduce=False, size_average=False)
input = Variable(torch.randn(3, 4))
target = Variable(torch.FloatTensor(3, 4).random_(2))
loss = loss_fn(F.sigmoid(input), target)
print(input); print(target); print(loss)BCEWithLogitsLoss:
上面的 nn.BCELoss 需要手动加上一个 Sigmoid 层,这里是结合了两者,不需要加sigmoid层,就能得到BCELoss一样的结果。
loss_fn = torch.nn.BCELoss(reduce=False, size_average=False)
input = Variable(torch.randn(3, 4))
target = Variable(torch.FloatTensor(3, 4).random_(2))
loss = loss_fn(input, target)
print(input); print(target); print(loss)
- CrossEntropyLoss(交叉熵损失函数)

def prac_cross():
# weight = torch.Tensor([1, 2, 1, 1, 10])
loss_fn = torch.nn.CrossEntropyLoss(reduce=False, size_average=False)
input = Variable(torch.randn(3, 5)) # (batch_size, C)
target = Variable(torch.LongTensor(3).random_(5))
loss = loss_fn(input, target)
print(input)
print(target)
print(loss)
print('---手算第一个---')
import math
exp = math.e
sigma_exp_x = pow(exp, input[0][0]) + pow(exp, input[0][1]) + pow(exp, input[0][2]) + pow(exp, input[0][3]) + pow(exp, input[0][4])
log_sigma_exp_x = math.log(sigma_exp_x)
loss_1 = -input[0][2] + log_sigma_exp_x
print('第一个样本的loss:', loss_1)假设共有三个类别cat、dog、bird,那么一张cat的图片标签应该为 。并且训练过程中,这张cat的图片经过网络后得到三个类别网络的输出分别为3、1、-3。那么经过softmax可以得到对应的概率值,如下图:
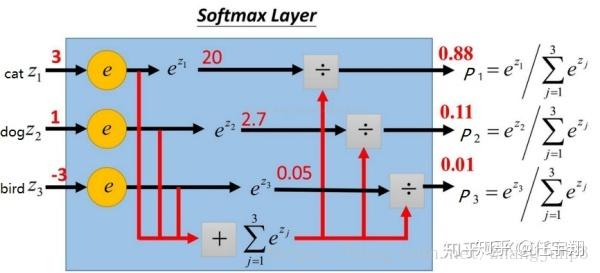
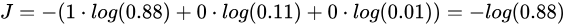
- Hinge Loss(折页损失函数)
参考文献:
http://www.10tiao.com/html/782/201806/2247495489/1.html
https://www.cnblogs.com/massquantity/p/8964029.html
https://blog.csdn.net/shanglianlm/article/details/85019768
https://blog.csdn.net/zhangjunp3/article/details/80467350
https://blog.csdn.net/zhangxb35
除了MSE,MAE,huber loss,在回归任务中,我们还会使用log-cosh loss,它可以保证二阶导数的存在,有些优化算法会用到二阶导数,在xgboost中我们同样需要利用二阶导数;同时,我们还会用到分位数损失,希望能给不确定的度量。
除了log和hinge,在分类任务中,我们还有对比损失(contrastive loss)、softmax cross-entropy loss、中心损失(center loss)等损失函数,它们一般用在神经网络中。
lossfunction多样性的背后实际上是靠着一类叫做随机梯度下降(SGD)的优化算法作为支撑,随机梯度下降的优越性绝不是为了减小时间效率,而是机器学习伟大的创新之一,我们将在下一节介绍以SGD为代表的优化算法。
均方误差(MSE):是回归问题中最常被使用的损失函数.
posted on 2019-09-04 11:32 Sanny.Liu-CV&&ML 阅读(9107) 评论(0) 编辑 收藏 举报





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现