全局光照
（1）双向反射分布函数 BRDF（Bidirectional Reflectance Distribution Function）
我从某个方向进来，并且反射到某个方向去，这个能量是多少？
在此之前，我们先研究下反射到底是怎么回事。
光从一个方向进来，打到一个物体，然后被弹走了，改变一个方向，这是一种理解。
也可以理解成，光线打到了某一个物体表面，被吸收了，被吸收了后再从这个物体表面把这部分能量发出去。经过了一个中间过程。
对于一个小的块，单考虑从某一个方向的立体角乘以这个 Radiance，就可以得到这块接收到的 Irradiance 是多少。Irradiance 会转化成 Radiance 再出去。
对于这么一个小块，我知道它从某一个方向接收到了某些能量，然后我知道它要把能量辐射到四面八方去，但我不知道往某个方向辐射的能量是多少。那我们定义一个函数，专门来描述这个概念。对于任何一个出射方向，我算出它的 Radiance，然后除以这个小块接收到的 Irradiance，这就是 BRDF（Bidirectional Reflectance Distribution Function），它会告诉我们一个表面如何把一个方向收集到的能量反射到另一个方向上去。BRDF 就是吸收能量后往某一个方向出射的比例。
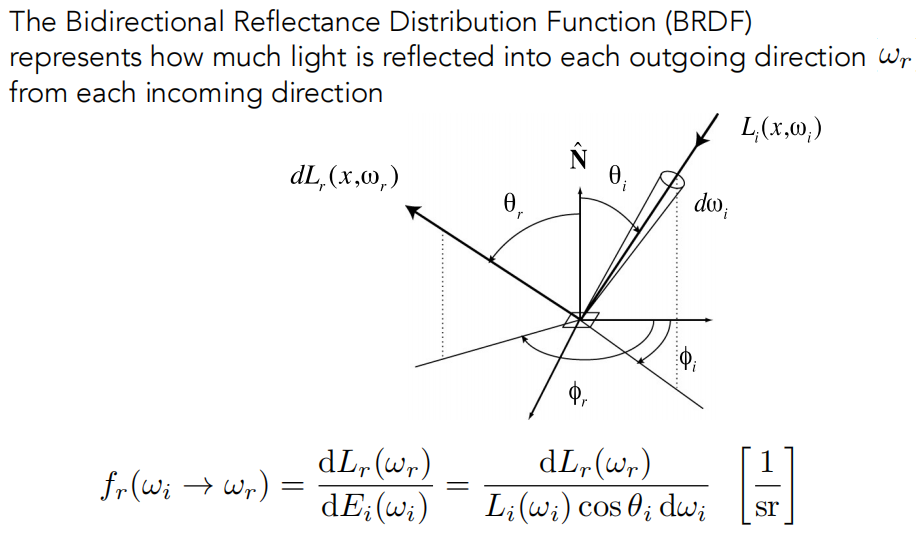
描述了光线和物体是如何作用的，它定义了物体的不同的材质是怎么回事。
BRDF 说明了从某一个方向进来的光反射到出射方向有多强。那我把每一个方向入射的光对于出射方向的贡献都给加起来，就可以得到这个点在所有可能的入射光下，最后反射到某个方向上是什么样的了。
（2）反射方程（Reflection Equation）
渐渐地从物理概念的定义就可以总结出来一些真正的光线传播的规律了。反射方程定义了一个着色点在各种不同的光照环境，即任何一个光照的入射方向，然后对我一个观测的方向的贡献。
后面三项就是这个小块收到的 Irradiance，那么它的 Irradiance 乘以 BRDF 就会变成出射的 Radiance。
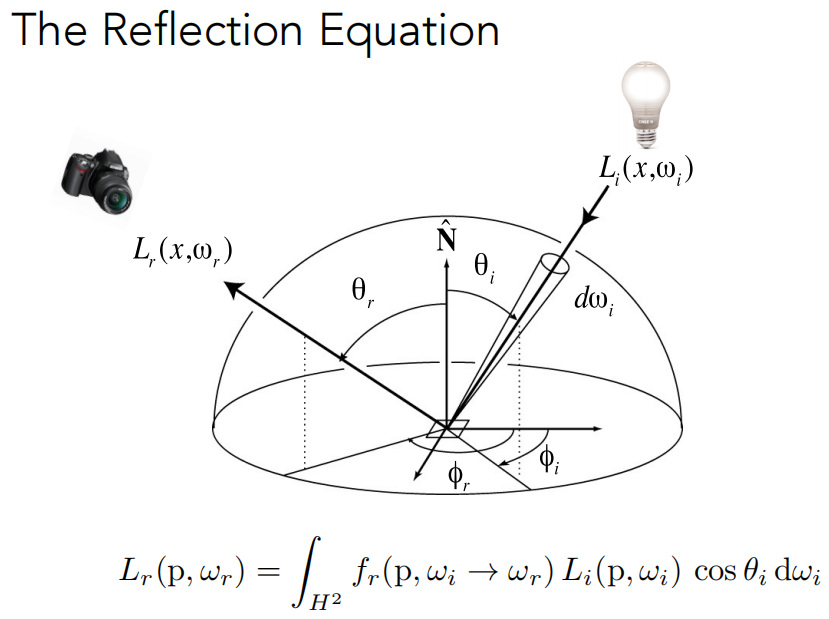
反射方程告诉我们，我要从某个点观察某一个着色点，那我要考虑能够到达这个着色点的所有的光线，可不是只有光源能到达这个点，其它的物体也会被光源所照亮，也会反射光进来，就是说，我考虑的 Radiance 可不只是光源，也可能是别的物体反射一次后出去的 Radiance。那么这件事越想就越想到递归了，就是说任意一个面，它接受到光源的照射，它会反射出去一些 Radiance，这些 Radiance 又会用来照亮其它的着色点。所以它是一个递归的问题。
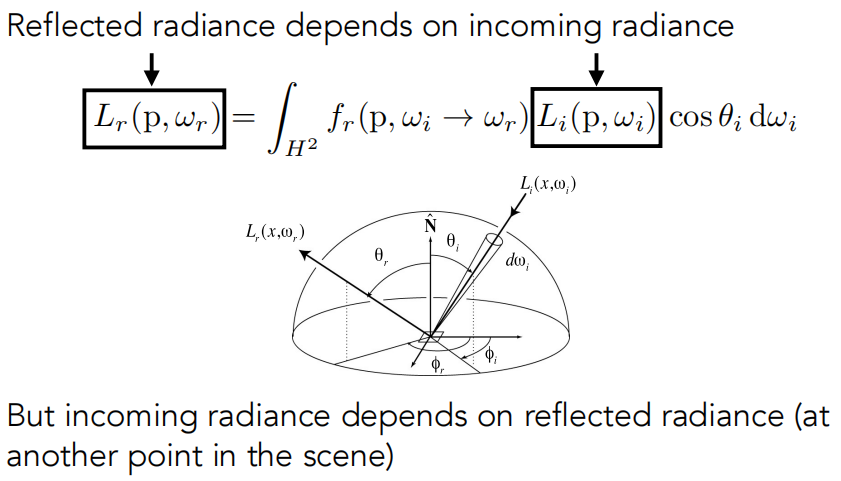
（3）渲染方程（Rendering Equation）
从反射方程要推出一个更加通用的方程，即渲染方程（Rendering Equation）
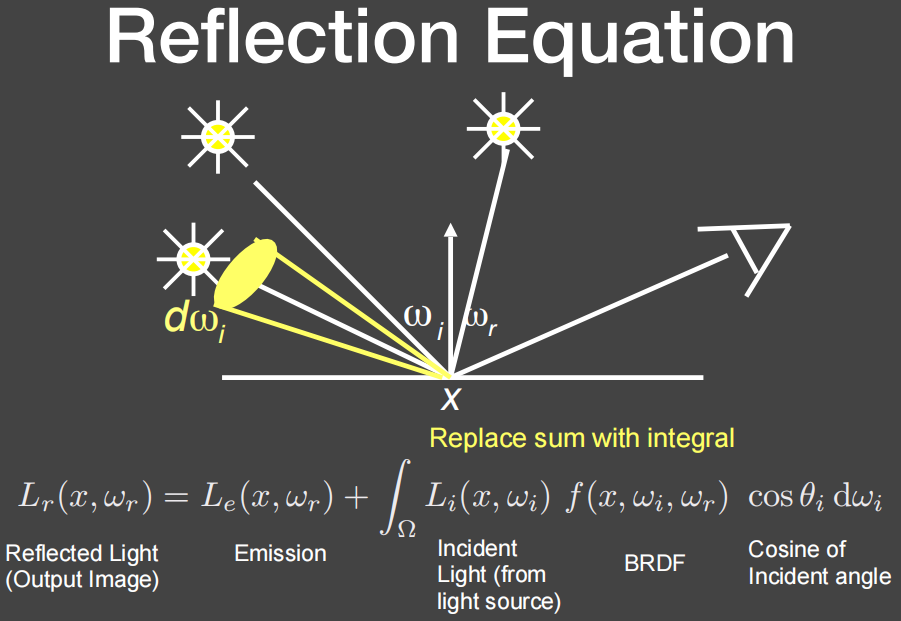
就是如果这个物体还会自己发光，那就把这个发的光加上就可以了。
那么这就是一个很完备的定义了，所有的光线传播都可以用这个渲染方程来总结。
跟 Blinn-Phong 模型一样，我们假设所有方向都朝外，那么比如说 ωi ，我们分明知道它是从别的地方打到这个点的，但我们写做 ωi 还是向外。半球的定义写做 Ω+ ，或者 H2 ，假如有一个平面，法线向上，如果有一根光线从底下打到这点，如果我们考虑反射的话，这种情况是不可能的。这里我们通过限制积分域的方式表示下半球贡献是零。
这么一个渲染方程可以说是现代图形学的基础。
（4）全局光照
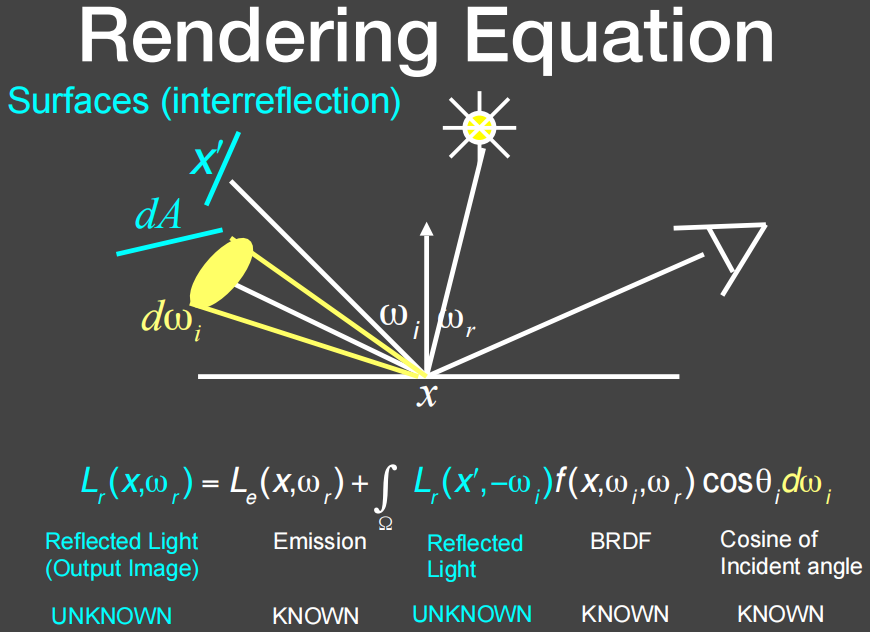
简化的递归方程。
进一步简写。对于所有的物体它辐射出来的所有的能量，等于所有光源辐射出来的能量，加上这些辐射出来的能量被反射之后的能量。
L 是递归定义的，解出 L。用到泰勒展开，分解成下面这样：我直接看到光源会看到什么（E），加上光源辐射出来的能量经过一次反射之后我会看到什么（KE），加上光源辐射出来的能量经过两次反射之后我会看到什么（K2E）...... 显然是对光线传播弹射次数的一种分解。
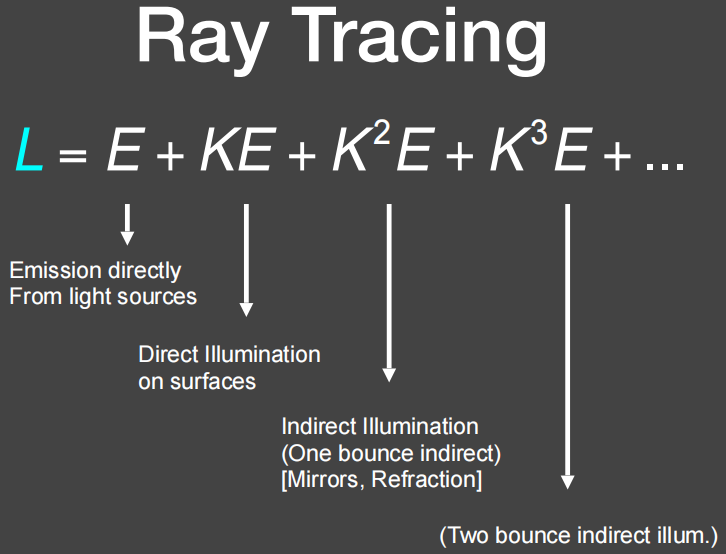
光线弹射一次得到的结果叫直接光照，光线弹射两次得到的结果叫间接光照...... 所有光线弹射次数全部加起来的结果就叫做全局光照。也就是说，全局光照不是等于间接光照，而是直接和间接光照的集合。
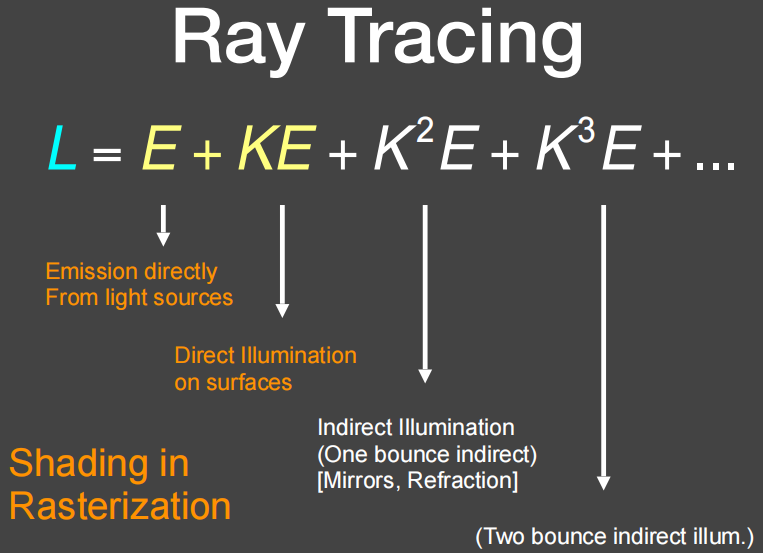
从另外一个角度上来理解这个式子。我们看光栅化可以做什么。光栅化可以把物体投影到屏幕上，屏幕上任何一个着色点的位置我知道，然后我知道光源的位置，我就可以做着色，着色就是直接光照，或者光源直接投射进屏幕上来，如果我能看到光源的话。就是说，光栅化就是光源自己和直接光照部分，后面的部分就是光栅化比较难做的。这也是另一个理由我们要用光线追踪的方法来解决光线传播问题，因为它可以很容易的做后面的部分，即间接光照的部分。
