光线追踪及其加速结构
(1)为什么会有光线追踪(Ray Tracing)?
光栅化不能很好地表现全局的效果。如软阴影、毛玻璃效果、间接光照。光线打到一个物体,然后反射打到另一个物体,然后打到人的眼睛。如窗外的光打到地板上,漫反射又打到墙壁上,漫反射又打到任何位置上,不断地弹射最后才打到人的眼睛里去。光线在到达人眼之前弹射不止一次。


光线追踪非常慢
一帧就需要花费 1 万个 CPU 小时。

光线(Light Rays)的定义
光线沿直线传播的;两个光线各传播各的,不会发生碰撞;光线从光源出发到达我们的眼睛(光路可逆)。
“当你凝视深渊,深渊也在凝视着你”


光线投射(Ray Casting)
根据光路距离判断阴影,之前说过。
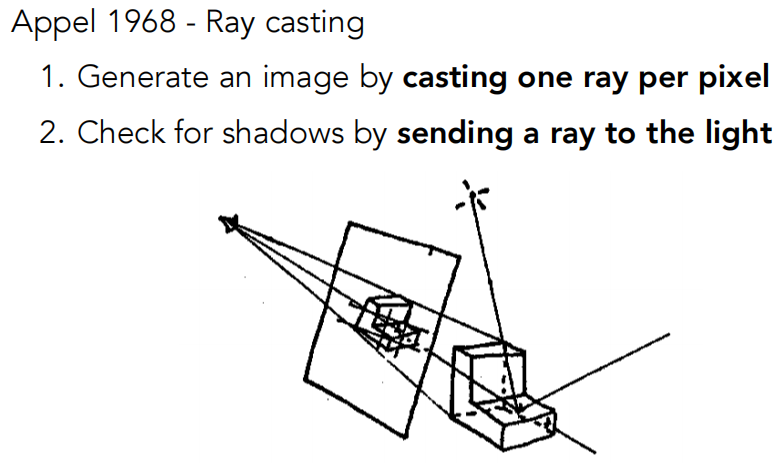
光线总要考虑与场景中最近的点

并且该点与光源之间不能有物体阻挡。黑色的箭头是在这一点的法线。
有了法线、入射方向和出射方向,就可以计算这一点的着色。就可以写入屏幕上这个像素的值。

然后就可以得到和光栅化近似相同的结果
(2)Whitted-Style 的光线追踪

那么是如何做到的呢?
光线打到一个玻璃球,有一部分能量要被反射掉:
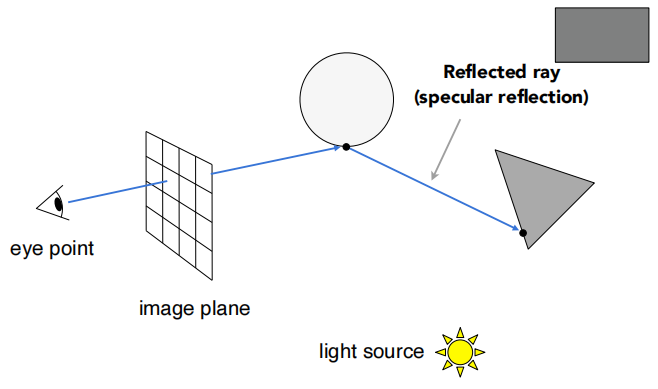
有一部分要被折射进去,并且可以继续传播:
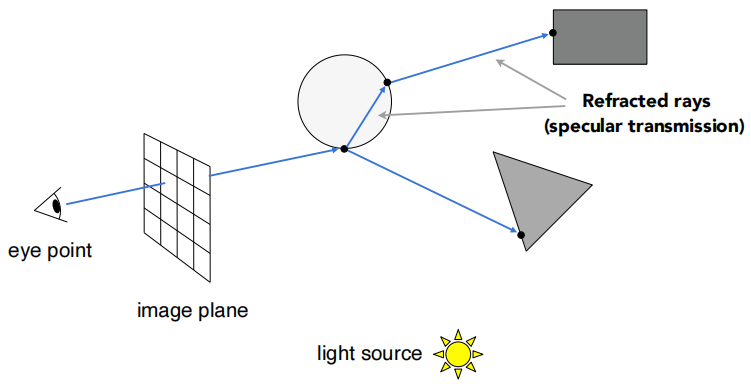
由于光线弹射次数多了,我在每一个点都要去计算着色的值。
如果我的光源可以照亮任何一个弹射的点,那我就把我算出的着色的值最后都给加到那一个像素的值里面去。

定义不同的光线类型:
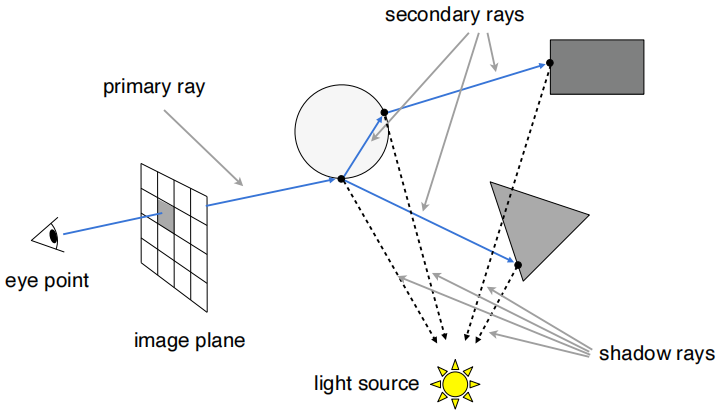

(3)光线打到物体表面的交点怎么求?
光线的几何定义:

定义:球上的任何一个点 p 到球心 c 的距离,都等于半径 R。
点 p 既在光线上,又在球上,那这两个方程都要满足。

方程中不知道的是 t,即传播多久能打到这个位置。可以解出这个公式:
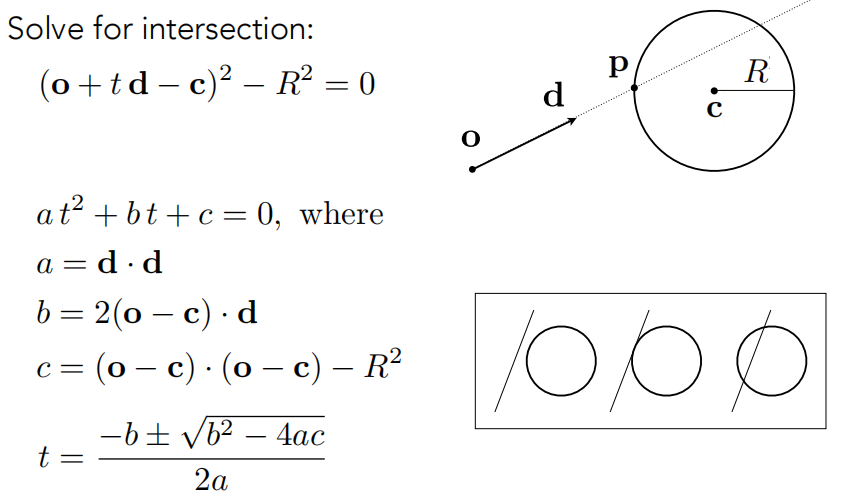
根据解的数量,有相离、相切、相交的情况。就可以解出不同的点。
推广到光线和一般性的隐式表面的求交:

把 t 解出来,就可以得到光线与各种各样不同的隐式表面求交。
对于显式表面怎么做?
交点数量是奇数则光线在物体内,交点数量是偶数在物体外。

判断光线是否和物体有交点,那就将三角形一个一个求交,可行但非常慢。
怎样求光线和三角形的交点。三角形肯定在一个平面内,先找到光线和这个平面的交点,再判断这个交点在不在三角形内。点在不在三角形内前面已经讲过。

可以用一个方向和一个点来定义平面

如何将平面上的任何一个点用 p' 和 N 表示?就像光线上的任何一个点能用 o + td 的形式表示。
满足 pp' 这个向量与法线 N 是垂直的,即可定义。展开了之后就是 ax + by + cz + d = 0,很显然这就是平面的方程。
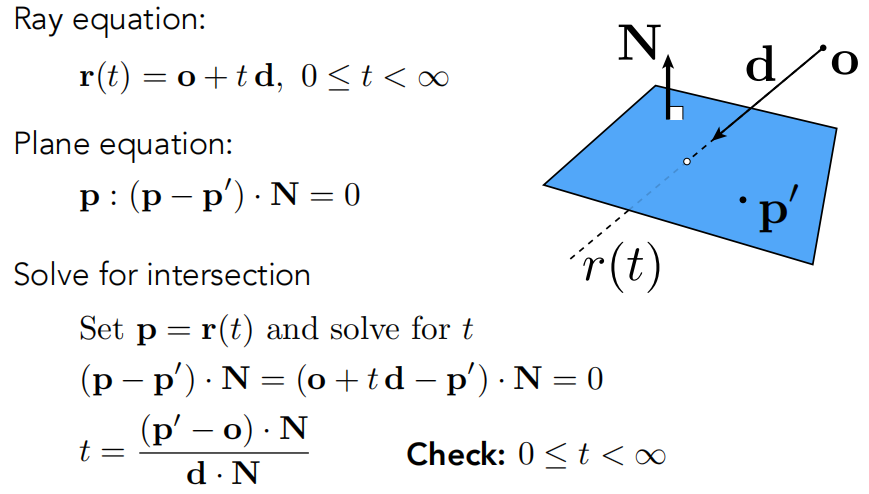
又回到了刚才的做法,解出 t,下一步就是判断这个点是否在三角形内就可以了。
但是人们是偷懒的,有没有一种办法我能一下解出光线与三角形的交点?

用重心坐标描述的位置,只要这三个系数加起来等于一,我们就可以得到任意一个在这三个点所定义的三角形所在的平面内的点。所以等式右边就是用重心坐标表示的平面内的任意一个点。
因为向量都是在三维空间的,一个都有三个数,可以写成三个式子,有三个未知量 t、b1、b2,当然可以把它解出来。解出来就是根据克莱姆法则所列成的上述式子。
我怎么知道解出来的就是在三角形内呢?三个系数都要是非负的,即直接通过重心坐标就可以定义点在三角形内。
把每个三角形都与光线求交,速度很慢,我们怎么把速度提上去?

像下面的场景就绝对不能用上面最原始的方法来做:数千万个三角形


(4)加速结构
包围盒(Bounding Volumes)
用一个相对简单的形状将一个复杂的物体包起来。
有一个简单的概念,如果光线连包围盒都碰不到,那就更不可能碰到包围盒里面的物体了。

长方体就是由三个对面形成的交集:前后、左右、上下
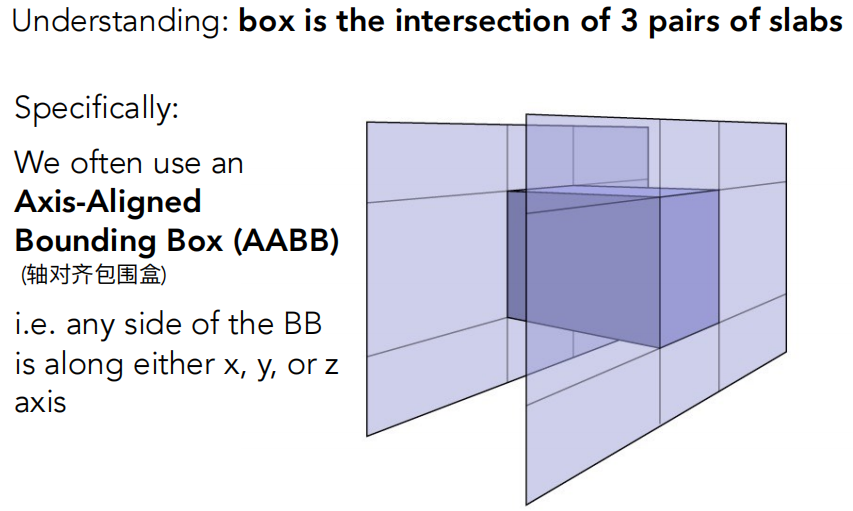
如何判断光线和包围盒是否有交点?先看二维上怎么做
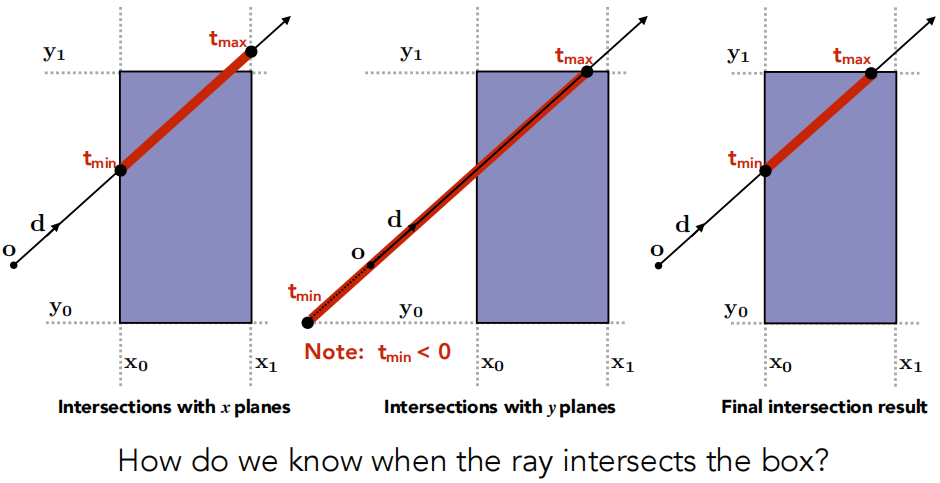
对于两条竖直的线,在什么时刻会有交点;对于两条水平的线,在什么时刻会有交点。对于任何一个对面,我都可以求出光线进去的时间和出去的时间。那么对于这个盒子来说,我是什么时候进入和什么时候出去呢?即对这两个线段求了一个交集。
可以直接拓展到三维情况:

那么什么时候有交点呢?如果进入的时刻小于出去的时刻就有交点。
如果 texit < 0,那么包围盒在光线的背后;如果 texit ≥ 0 并且 tenter < 0,那么光线起点就在盒子内。
iff 是当且仅当(if and only if)。

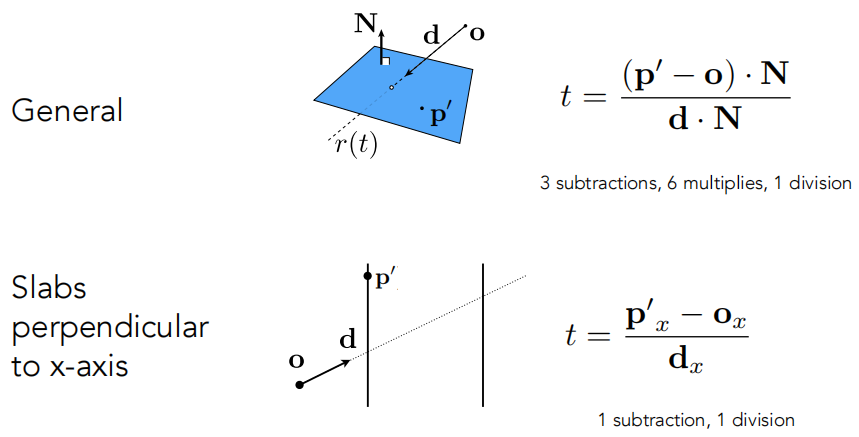
为什么要“轴对齐”?方便计算:
利用光线对包围盒求交来加速光线追踪
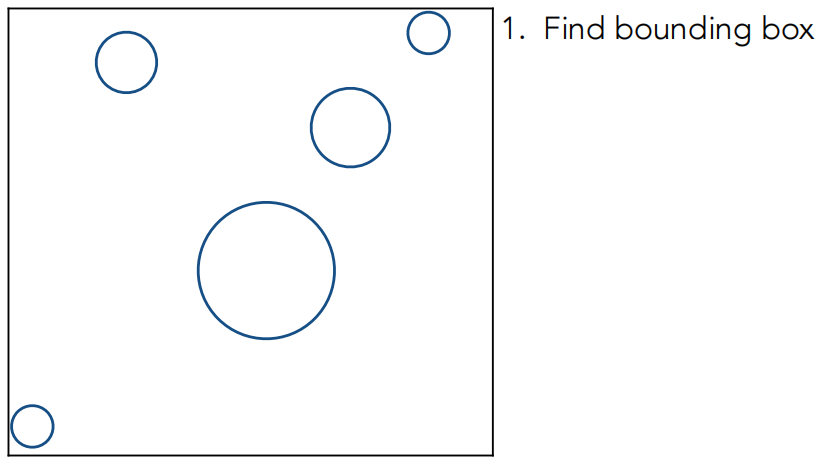


对包围盒的预处理完成。一束光线射进包围盒,判断光线是否有可能与格子内的物体有交点。
只要做若干次光线与盒子的求交,可以避免与场景中的所有物体求交。

先看看划分成一个格子,没有任何加速的意义。

格子太密集了,就要做好多次光线与格子的求交,效率就下去了。

只要知道这里有一个平衡就可以,格子不能太稀疏,也不能太密集。

在这个场景中,各个地方都有几何的物体,分布就比较均匀,用格子的效果就比较好。

而对于这个场景,空的地方太多了,物体分布挺不均匀的,就不适合用均匀的格子来解决问题。

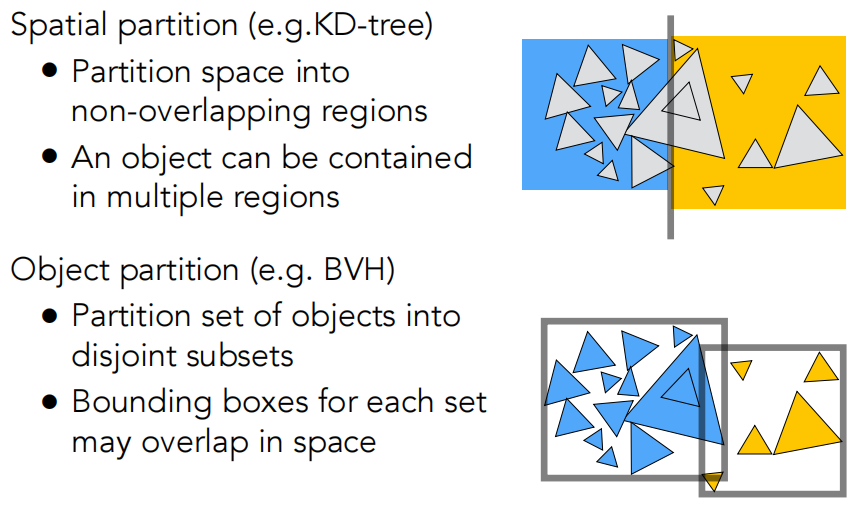
空间划分(Spatial Partitions)
这个问题当然并不是最早从图形学上产生的。
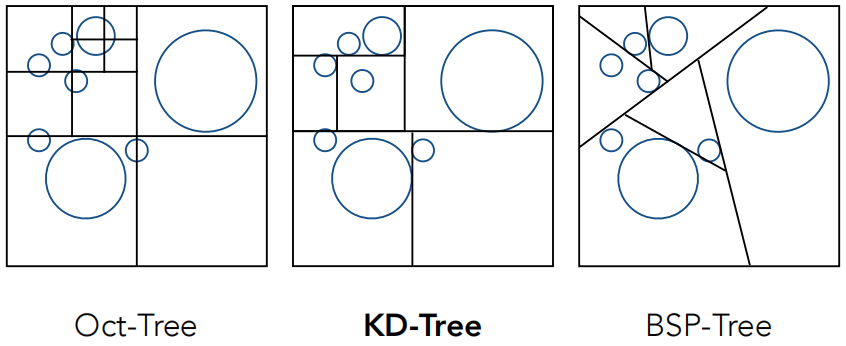
Oct-Tree(八叉树):把整个场景先想办法包起来,然后把这个包围盒切成八份,因为它是空间中的包围盒,类似一块豆腐。八叉树在二维情况下其实是四叉树,对每一个子节点,然后又把它切成四份,图上只把一个地方继续进行切份,其实其他的地方同样要继续进行下去。到什么时候停止呢?比如我可以定一个规则,当切成四块后有三块都与物体不相交。也就是说,停下来是取决于各种不同的标准。但是人们不喜欢用八叉树,因为它和维度绑定了,三维情况下是八叉树,思维情况下就是 24 = 16 叉树。
KD-Tree:每次只沿一个轴把它砍开,就砍一刀。比如先水平一刀,形成了上下两块,我再在两块分别竖直一刀...三维情况下就是沿着 x、y、z 三个轴用平面砍开。
BSP-Tree:对空间进行二分的方法。每一次选一个方向进行划分,速度肯定赶不上 KD-Tree。并且它在维度高的时候仍然越来越不好计算的问题,到了四维及以上就要用超平面进行砍开,越来越复杂。
以 KD-Tree 为例
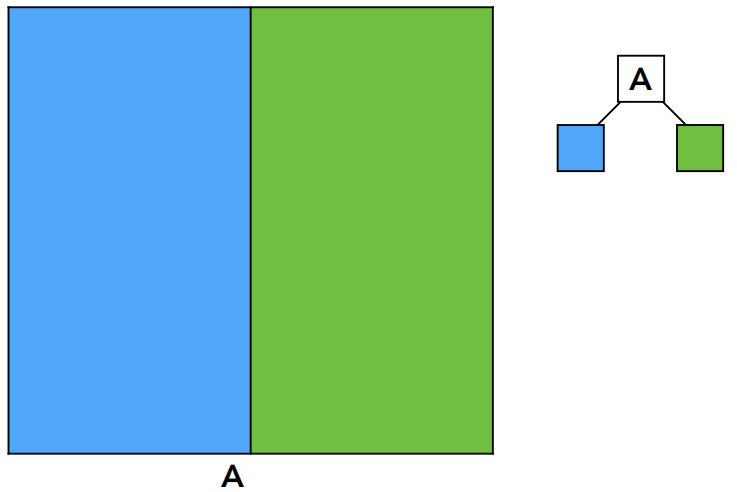
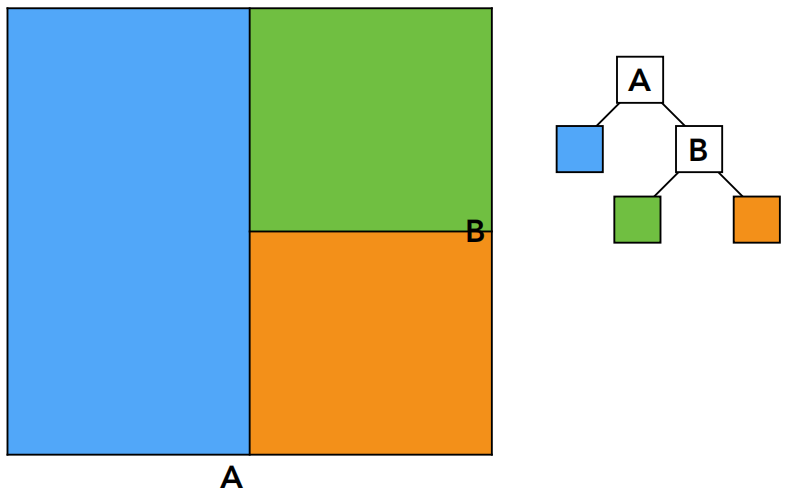

KD-Tree 的数据结构:
只存储在叶子节点上

那么这个结构实际上应该如何做光线追踪的加速?
一束光线射进包围盒

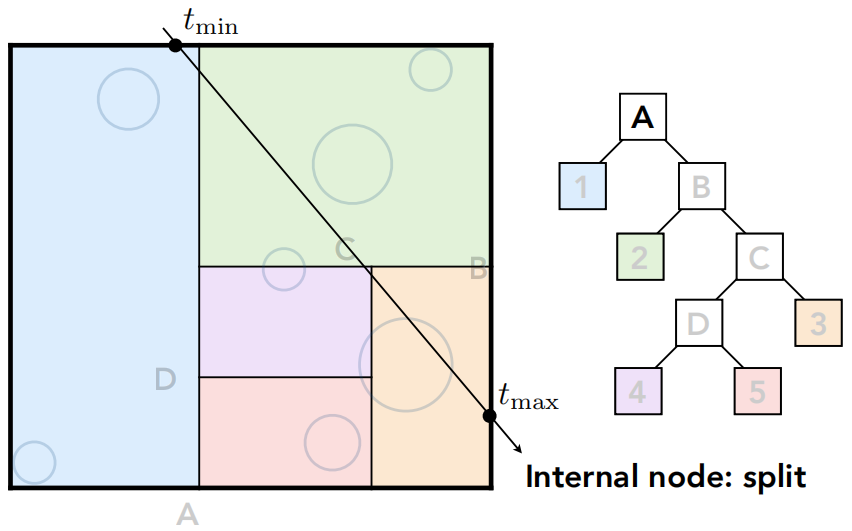
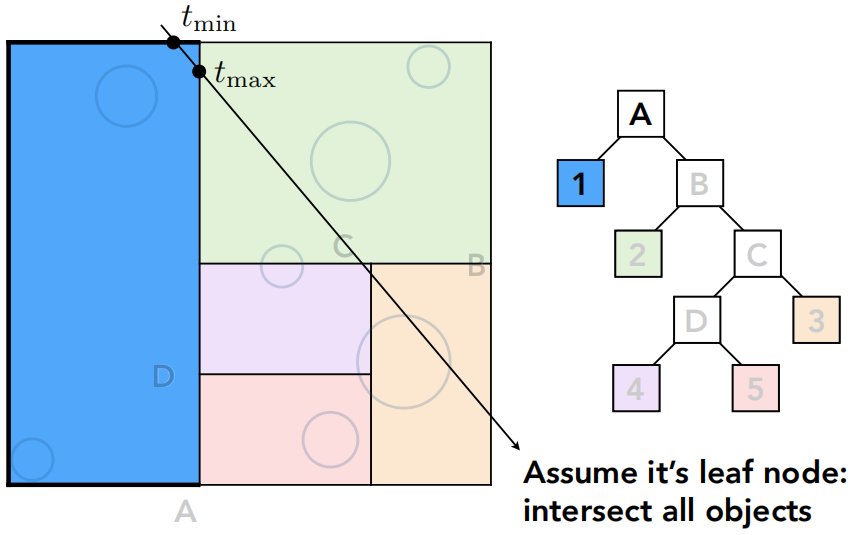
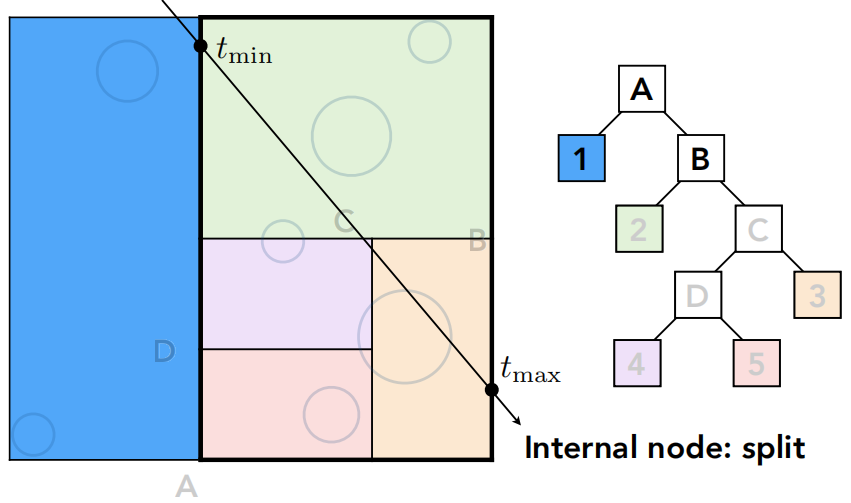
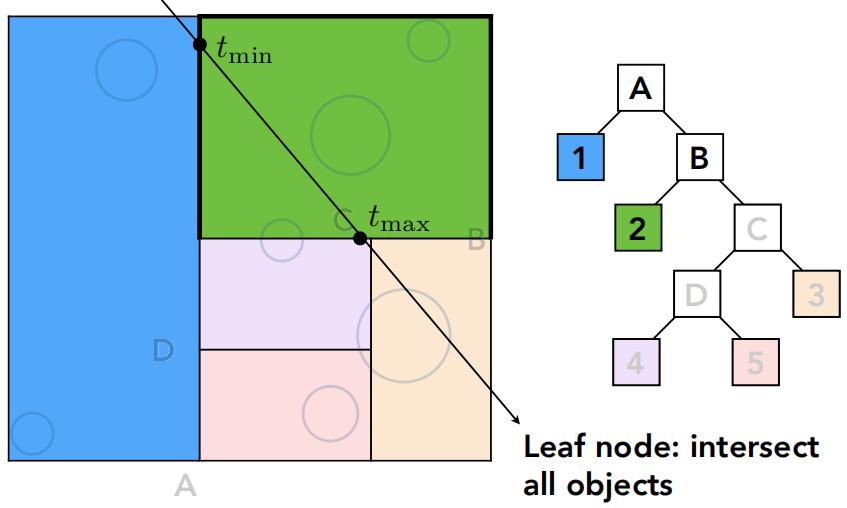

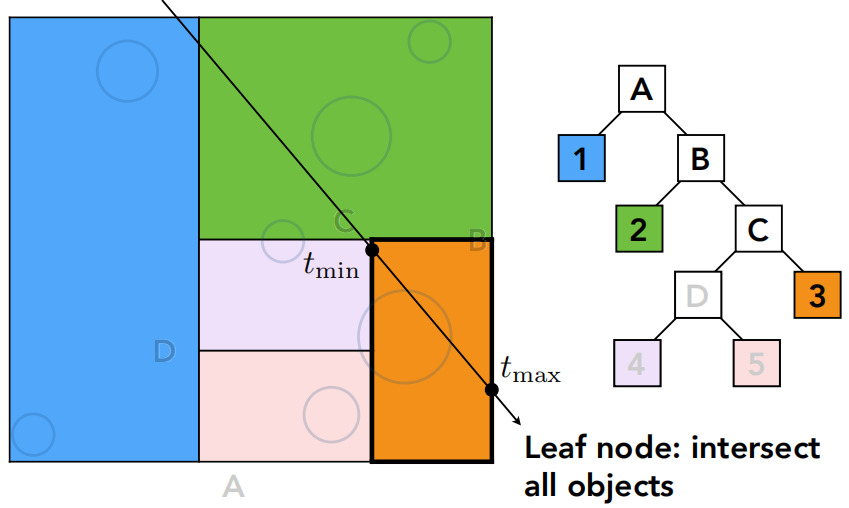

如果光线和某一个盒子没有交点,那什么都不用做,如果有交点,那我就知道光线和它的两个子节点可能都有交点,所以都判一下,直到光线打到叶子节点,就要和叶子节点里的所有物体求一次交。
但是 KD-Tree 有一些缺点:比如同一个物体会与多个格子相交,三角形和不同格子的交集很难判断。最近十年,人们就渐渐不用这个 KD-Tree 了。
通过物体来划分(Object Partitions),通过这种划分形成的加速结构称为 Bounding Volume Hierarchy(BVH)。这种结构得到了非常非常广泛的应用。在图形学中,不管是做实时还是离线光线追踪,大家用的都是这么一种结构。因为它解决了 KD-Tree 的这两个问题。
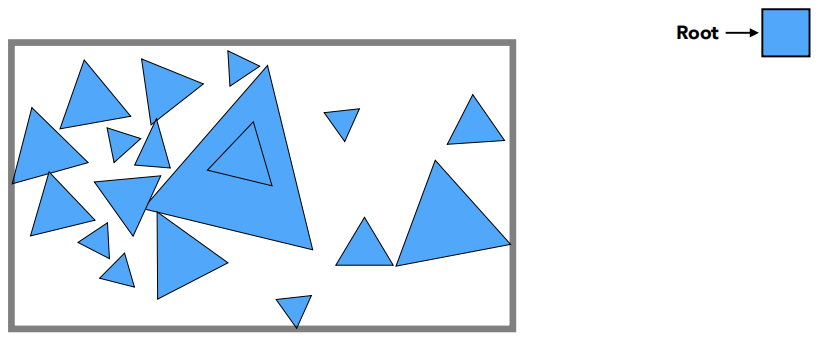
划分成两部分,分别去求一下它们的包围盒

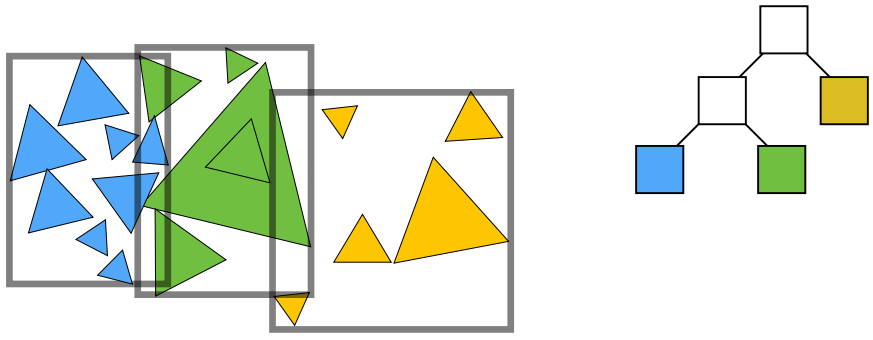
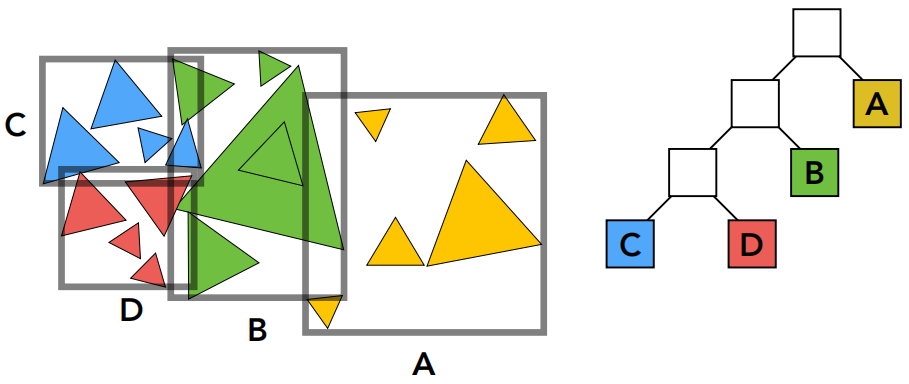
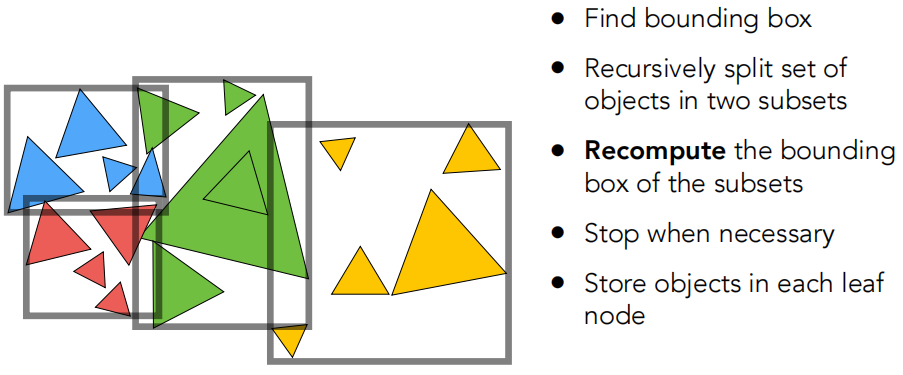
不同的物体在不同的包围盒内,并且省去了三角形和各包围盒求交的过程。但是 BVS 并不是将这些包围盒严格划分开。

判断光线与 BVH 求交的伪代码:

空间划分和物体划分的比较: