决策表测试
（1）决策表元素
在上图给出的决策表中，如果 C1、C2 和 C3 都为真，则采取行动 A1 和 A2 。如果 C1 和 C2 都为真而 C3 为假，则采取行动 A1 和 A3 。
在 C1 为真 C2 为假条件下，规则中的 C3 条目叫做“不关心”条目。不关心条目由两种主要解释：条件无关或条件不适用。
如果有二叉条件（ 真 / 假，是 / 否，0 / 1 ），则决策表的条件部分类似于真值表，n 个条件的组合有 2 ^ n 。（ 两个二叉条件的组合：2 ^ 2 => 00、01、10、11 ）
所有条件都是二叉条件的决策表叫做有限条目决策表。如果条件可以有多个值，则对应的决策表叫做扩展条件。
决策表结构能够保证我们考虑所有可能的条件值组合。如果使用决策表设计测试用例，那么决策表的这种完备性质能够保证一种完备的测试。
为了使用决策表标识测试用例，我们把条件解释为输入，把行动解释为输出。
（2）三角形问题的决策表
将条件 C1 扩展为三角形特性的三个不等式。则改进后的三角形问题表如下：
（3）NextDate 问题的决策表
选择 NextDate 函数，因为它可以说明输入定义域中的依赖性问题。而决策表可以突出这种依赖关系。
如果变量确实是独立的，则使用类的笛卡尔积是有意义的。如果变量之间在输入定义域中存在逻辑依赖关系，则这些依赖关系在笛卡尔积中就会丢失。
决策表通过使用“不可能行动”概念表示条件的不可能组合，使我们能强调这种依赖关系。（ 注意“不可能”与“非法输入”之间的区别 ）
1）第一次尝试：有限条目决策表
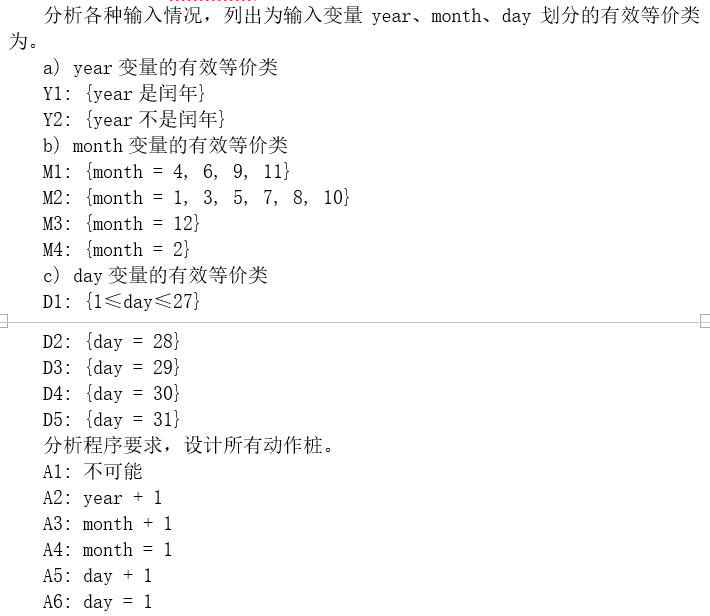
首先，可以从等价类集合开始。
如果我们希望突出不可能的组合，则可以建立条件和行动的有限条目决策表。在这个决策表中会有 256 条（ 2 ^ 8 ，Y1 和 Y2 写作一条 ）规则，其中很多是不可能的。
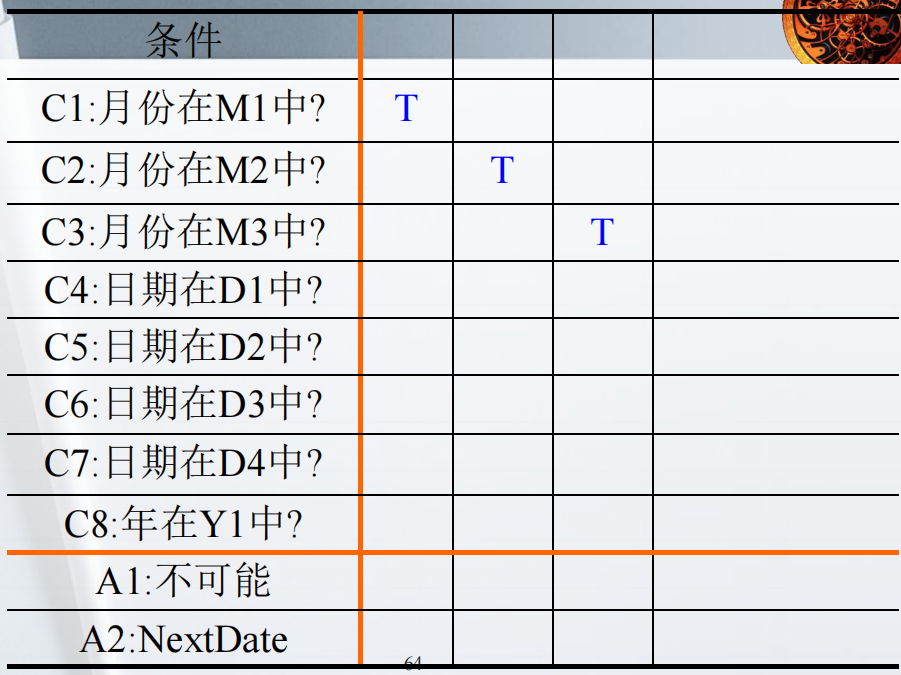
考虑到月份变量相互排斥，可以写作：
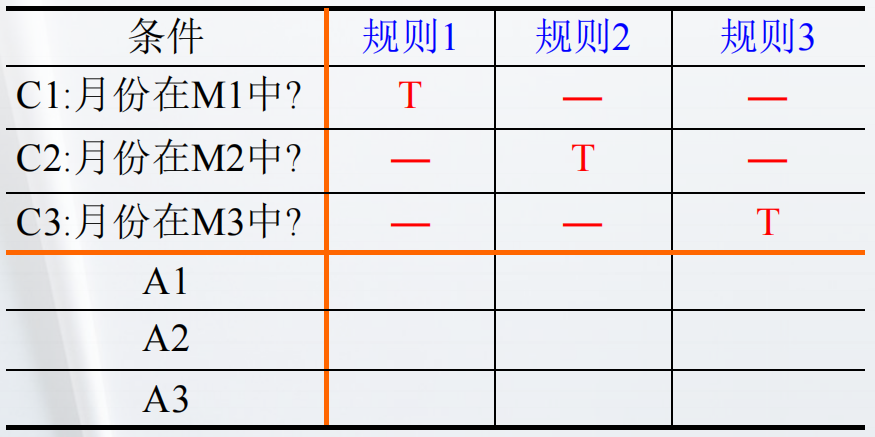
对于以上的决策表（ 有限条目决策表 ），如果有 n 个条件，则有 2 ^ n 条规则。（ 类似于真值表 00、01、10、11 ）
没有不关心条目的规则则统计为 1 条规则；规则中每出现一个不关心条目，它实际包含的规则数乘 2 。（ 一个不关心条目可能是 T / F ，因此一个规则中每出现一个不关心条目，就要乘以 2 ）
对于 3 个条件，我们得到的规则条数就为 12 条，但实际上，有 3 个条件，则应该有 8 条规则（ 2×2×2 ）。为了找到问题所在，我们扩展了含有不关心条目的规则：
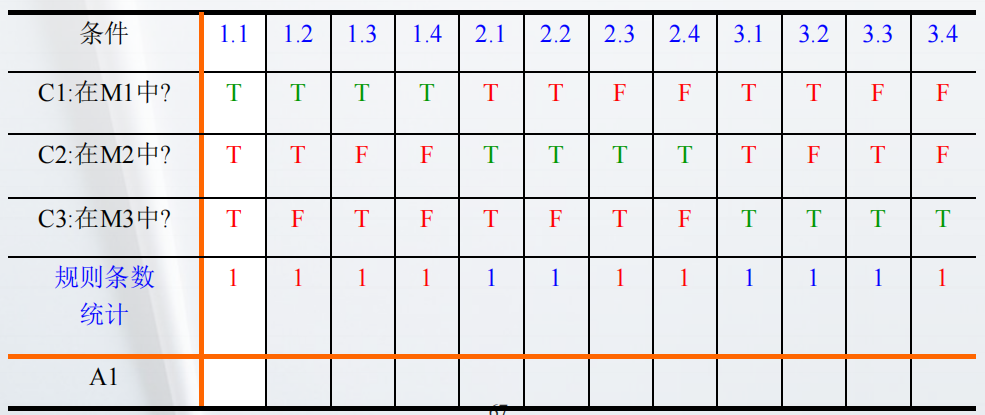
有点懵，所以说用有限条目决策法的定义来套 NextDate 问题是行不通的。
2）第二次尝试：扩展条目决策法
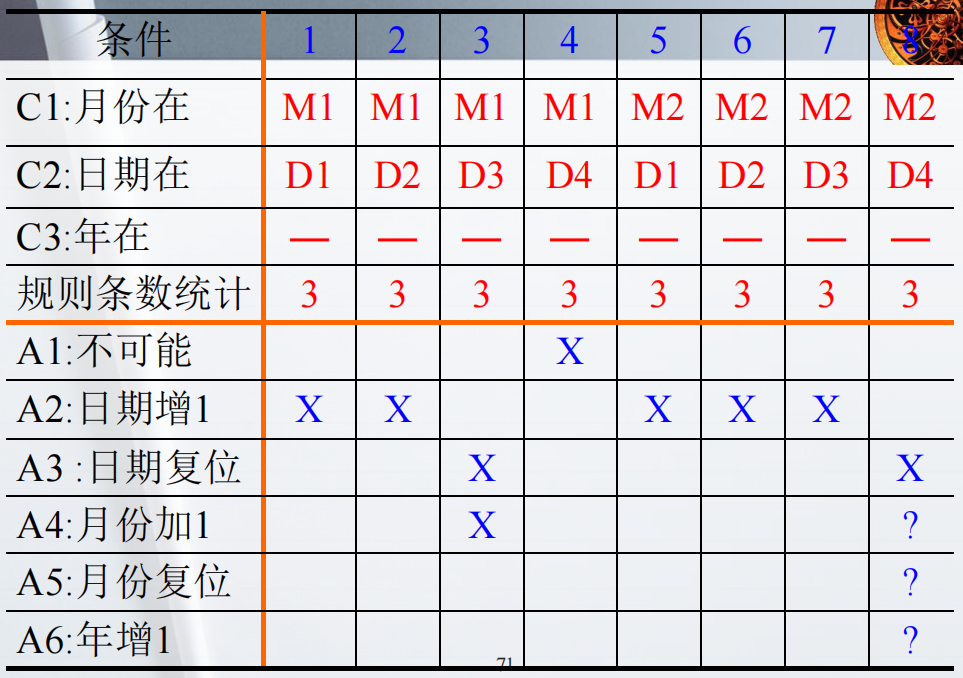
在构建扩展条目决策表时，必须保证等价类构成输入定义域的真划分。如果规则条目之间存在“重叠”，则会存在冗余情况，使得多个规则都能够满足。
3）第三次尝试
（4）指导方针
