树链剖分入门详解+入门题推荐
以前没有接触过树链剖分的同学们看到这个东西是不是觉得很高大上呢，下面我将带你们进入树的世界（讲得不好别打我）
首先我们来看一道题
这道题的大意是，每个软件有一个父软件（除根节点外）。要安装一个软件必须先安装它的父软件，要卸载一个软件必须先卸载它的所有子软件，模拟对软件的安装和卸载操作
通过以上的分析，我们可以看出这大概是一个树形结构。
由于节点个数和操作次数的范围为\(1e5\),明显要用一个\(nlgn\)或者\(nlg^2n\)的算法，那么就可以引出我们今天的主角——树剖了。
树链剖分
顾名思义，树链剖分就是指将一颗树分成若干条链，使得可以使用数据结构（例如线段树，主席树）来进行维护
它的特点很明显，我们可以非常便捷的处理同一条链上的若干点和边
直说上面大概会让大家一头雾水，这只是让大家对树剖有一个初步的概念，下面我们要开始正式的讲解了
先下若干定义
重儿子：子树最大的儿子
轻儿子：除了重儿子以外的儿子
重边：父节点与重儿子组成的边
轻边：除重边以外的边
重链：重边连接而成的链
轻链：轻边连接而成的链
链头：一条链上深度最小的点
下图为例
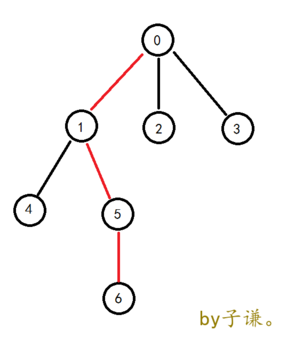
图中的红色边即为重边，重边连成的链，与红色边相连的所有节点，即为重儿子，0节点即为链头
重链未必只有一条，每个子树都至少有一条重链，如下图
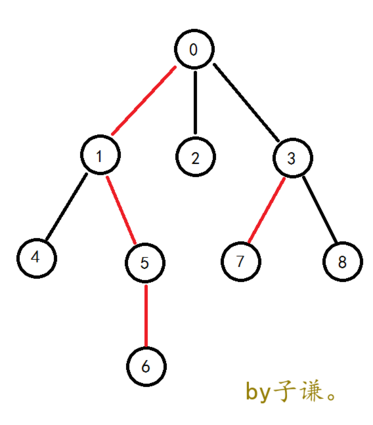
我们默认已经将链分好了，我们来说一下树剖的相关操作
一般，我们需要用树剖来解决以下问题
修改点x到点y路径上各点的值
查询点x到点y路径上各点的值
修改点x子树上各点的值
查询点x子树上各点的值
首先我们要对每个节点进行编号，保证在链上的节点编号是连续的，这样子树的编号也是连续的
那么我们每次对\(x，y\)两个点进行询问
若两点在同一条链上，则直接在线段树上进行询问
若不在一条链上，则每次选择链头深度更大的一个往上跳，直到两点在同一条链上
那么对于子树的操作我们怎么搞呢？
很简单，我们已经说了，子树的编号是连续的，根节点的编号到加上子树大小-1的区间即为子树区间
大概是这个样子，我们再回过头来看开头的那道题
我们直接放代码吧
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cctype>
#define ll long long
#define gc() getchar()
#define maxn 100005
using namespace std;
inline ll read(){
ll a=0;int f=0;char p=gc();
while(!isdigit(p)){f|=p=='-';p=gc();}
while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=gc();}
return f?-a:a;
}
void write(ll a){
if(a>9)write(a/10);
putchar(a%10+'0');
}
int n,m;
struct ahaha1{ //首先，我们把依赖与被依赖的关系转化为边存起来
int to,next;
}e[maxn];int tot,head[maxn];
inline void add(int u,int v){
e[tot].to=v;e[tot].next=head[u];head[u]=tot++;
}
int f[maxn],sz[maxn],dep[maxn],son[maxn]; //f数组存储当前节点的父节点，sz数组表示以当前节点为根的子树大小，dep数组表示节点深度，son数组表示节点的重儿子
void dfs(int u,int fa){
int maxa=0;sz[u]=1; //sz初始为1，也就是仅包含自身
for(int i=head[u];~i;i=e[i].next){ //遍历所有子节点
int v=e[i].to;if(v==fa)continue;
f[v]=u;dep[v]=dep[u]+1;
dfs(v,u);sz[u]+=sz[v];
if(sz[v]>maxa)maxa=sz[v],son[u]=v; //不断修改重儿子，保证为子树最大的子节点
}
}
int b[maxn],in[maxn],top[maxn]; //b数组存储当前编号对应的节点，in数组表示当前节点的编号，top数组表示当前节点所处链的链头
void dfs(int u,int fa,int topf){
b[++tot]=u;in[u]=tot;top[u]=topf;
if(!son[u])return;
dfs(son[u],u,topf); //与重儿子相连的边为重边，所以链头不变
for(int i=head[u];~i;i=e[i].next){
int v=e[i].to;if(v==fa||v==son[u])continue;
dfs(v,u,v); //与其他儿子所连的边为轻边，所以链头变为轻儿子
}
}
struct ahaha2{
int v,lz;
ahaha2(){lz=-1;}
}t[maxn<<2];
#define lc p<<1
#define rc p<<1|1
inline void pushup(int p){
t[p].v=t[lc].v+t[rc].v;
}
inline void pushdown(int p,int l,int r){
int m=l+r>>1;
t[lc].v=t[p].lz?m-l+1:0;t[lc].lz=t[p].lz;
t[rc].v=t[p].lz?r-m:0;t[rc].lz=t[p].lz;
t[p].lz=-1;
}
int update(int p,int l,int r,int L,int R,int z){ //合并了修改和查询操作
if(l>R||r<L)return 0;
if(L<=l&&r<=R){int q=t[p].v;t[p].v=z?r-l+1:0;t[p].lz=z;return q;}
int m=l+r>>1;if(t[p].lz!=-1)pushdown(p,l,r);
int l1=update(lc,l,m,L,R,z),r1=update(rc,m+1,r,L,R,z);
pushup(p);
return l1+r1;
}
inline void solve_1(){ //需要放的物品数等于相关物品数减去已经放的物品数
int x=read(),ans=0;
while(top[x]){
ans+=in[x]-in[top[x]]+1-update(1,1,n,in[top[x]],in[x],1);
x=f[top[x]];
}
ans+=in[x]-in[0]+1-update(1,1,n,in[0],in[x],1);
write(ans);
putchar('\n');
}
inline void solve_2(){ //需要拿走的物品数为子树上已安装的物品数
int x=read();
write(update(1,1,n,in[x],in[x]+sz[x]-1,0));
putchar('\n');
}
int main(){memset(head,-1,sizeof head);
n=read();
for(int i=1;i<n;++i){
int u=read();
add(u,i);
}
tot=0;dfs(0,-1);dfs(0,-1,0);
m=read();string zz;
for(int i=1;i<=m;++i){
cin>>zz;
switch(zz[0]){
case 'i':solve_1();break;
case 'u':solve_2();break;
}
}
return 0;
}
是不是很简单呢？想不想自己尝试一下其他题目？
下面推荐几道树剖入门题
当然，还有我们的模板题【模板】树链剖分
感谢您的阅览，不妨点个赞再走啊
