洛谷 P1471 方差

还是老习惯，先放题面

题目背景

滚粗了的HansBug在收拾旧数学书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻HansBug在一本数学书里面发现了一个神奇的数列，包含N个实数。他想算算这个数列的平均数和方差。

输入输出格式

输入格式：
第一行包含两个正整数N、M，分别表示数列中实数的个数和操作的个数。
第二行包含N个实数，其中第i个实数表示数列的第i项。
接下来M行，每行为一条操作，格式为以下两种之一：
操作1：1 x y k ，表示将第x到第y项每项加上k，k为一实数。
操作2：2 x y ，表示求出第x到第y项这一子数列的平均数。
操作3：3 x y ，表示求出第x到第y项这一子数列的方差。

输出格式：
输出包含若干行，每行为一个实数，即依次为每一次操作2或操作3所得的结果（所有结果四舍五入保留4位小数）。

输入输出样例

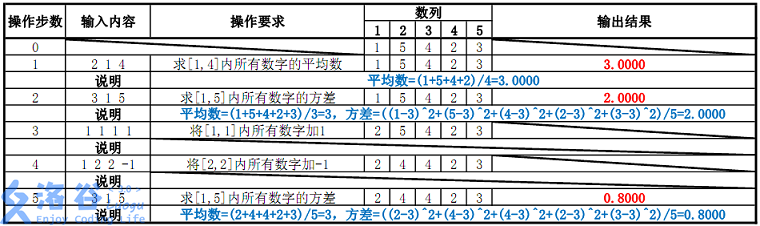
输入样例：
5 5
1 5 4 2 3
2 1 4
3 1 5
1 1 1 1
1 2 2 -1
3 1 5

输出样例：
3.0000
2.0000
0.8000

说明

样例说明：

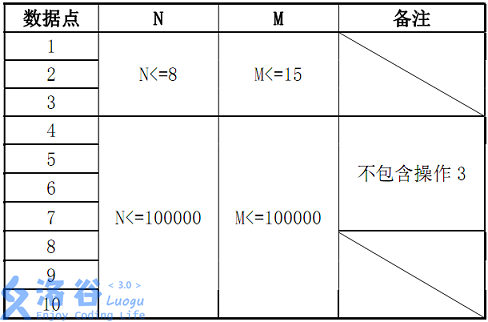
数据规模：

这道题并不能再说是线段树的模板题了，毕竟加入了数论元素 虽然还是很简单
这道题的难点就在于这个方差的修改，那么，我们来看看求方差的公式

\(s^2=\frac{(M-x_1)^2+(M-x_2)^2+(M-x_3)^2+···+(M-x_n)^2}{n}\)

这个公式看起来有点摸不着头脑对吧，没关系，我们转化一下

\(s^2=\frac{M^2-2*Mx_1+x_1^2+M^2-2*Mx_2+x_2^2+M^2-2*Mx_3+x_3^2+···+M^2-2*Mx_n+x_n^2}{n}\)

\(s^2=\frac{n*M^2-2*M(x_1+x_2+x_3+···+x_n)+x_1^2+x_2^2+x_3^2+···+x_n^2}{n}\)

\(s^2=\frac{x_1^2+x_2^2+x_3^2+···+x_n^2-n*M^2}{n}\)

看到这里是不是就比较清晰了，我们将复杂的方差的变换拆解了出来，化为了简单的平均数的运算与平方和的运算
求平方和的变换就容易许多了，还是看算式

\((x_1+p)^2+(x_2+p)^2+(x_3+p)^2+···+(x_n+p)^2\)

\(=x_1^2+2x_1p+p^2+x_2^2+2x_2p+p^2+x_3^2+2x_3p+p^2+···+x_n^2+2x_np+p^2\)

\(=x_1^2+x_2^2+x_3^2+···+x_n^2+2(x_1+x_2+x_3+···+x_n)p+np^2\)

这样也就比较明了了，直接上代码

#include<iostream>
#include<cstdio>
#include<cctype>
#define db double
#define ll long long
#define gc() getchar()
#define maxn 100005
using namespace std;

int n,m;
db a[maxn];
inline ll read(){
    ll a=0;char p=gc();int f=1;
    while(!isdigit(p)){f|=(p=='-');p=gc();}
    while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=gc();}
    return a*f;
}

struct ahaha{    //v表示元素和，q表示平方和
    double v,lz,q;
}t[maxn<<2];
#define lc p<<1
#define rc p<<1|1
inline void pushup(int p){
    t[p].v=t[lc].v+t[rc].v;
    t[p].q=t[lc].q+t[rc].q;
}
inline void pushdown(int p,int l,int r){    //修改参照公式
    if(!t[p].lz)return;
    int m=l+r>>1;
    t[lc].q+=2*t[lc].v*t[p].lz+(m-l+1)*t[p].lz*t[p].lz;
    t[rc].q+=2*t[rc].v*t[p].lz+(r-m)*t[p].lz*t[p].lz;
    t[lc].v+=(m-l+1)*t[p].lz;t[lc].lz+=t[p].lz;
    t[rc].v+=(r-m)*t[p].lz;t[rc].lz+=t[p].lz;
    t[p].lz=0;
}
void build(int p,int l,int r){
    if(l==r){t[p].v=a[l];t[p].q=a[l]*a[l];return;}
    int m=l+r>>1;
    build(lc,l,m);build(rc,m+1,r);
    pushup(p);
}
void update(int p,int l,int r,int L,int R,double z){
    if(l>R||r<L)return;
    if(L<=l&&r<=R){
        t[p].q+=2*t[p].v*z+(r-l+1)*z*z;   //平方和的修改参照公式理解
        t[p].v+=(r-l+1)*z;t[p].lz+=z;
        return;
    }
    int m=l+r>>1;pushdown(p,l,r);
    update(lc,l,m,L,R,z);update(rc,m+1,r,L,R,z);
    pushup(p);
}
double query1(int p,int l,int r,int L,int R){   //求区间和
    if(l>R||r<L)return 0;
    if(L<=l&&r<=R)return t[p].v;
    int m=l+r>>1;pushdown(p,l,r);
    return query1(lc,l,m,L,R)+query1(rc,m+1,r,L,R);
}
double query2(int p,int l,int r,int L,int R){    //求区间平方和
    if(l>R||r<L)return 0;
    if(L<=l&&r<=R)return t[p].q;
    int m=l+r>>1;pushdown(p,l,r);
    return query2(lc,l,m,L,R)+query2(rc,m+1,r,L,R);
}

inline void solve_1(){
    int x=read(),y=read();
    double z;scanf("%lf",&z);
    update(1,1,n,x,y,z);
}
inline void solve_2(){
    int x=read(),y=read();
    printf("%.4lf\n",query1(1,1,n,x,y)/(y-x+1));
}
inline void solve_3(){
    int x=read(),y=read();
    double t1=query1(1,1,n,x,y)/(y-x+1),t2=query2(1,1,n,x,y);
    printf("%.4lf\n",t2/(y-x+1)-t1*t1);
}

int main(){
    n=read();m=read();
    for(int i=1;i<=n;++i)scanf("%lf",&a[i]);
    build(1,1,n);
    for(int i=1;i<=m;++i){
        int zz=read();
        switch(zz){
            case 1:solve_1();break;
            case 2:solve_2();break;
            case 3:solve_3();break;
        }
    }
    return 0;
}