树状数组入门详解+题目推荐
在开始之前我们先来看一道题——题目链接
题目要求我们对数列进行单点加和区间求和两种操作
我们很容易想到每次直接加,求和时暴力求和即可。但是对于这道题,复杂度明显炸了。
那么我们考虑一下是什么影响了这种计算的效率呢?
对于单点加操作,我们直接用数组记录大小,直接修改,每次的复杂度为\(O(1)\),但是查询的复杂度就会是\(O(n)\)。这是我们不愿接受的。
对于区间求和操作,我们记录数列的前缀和,每次查询的复杂度就是\(O(1)\),但是单点加的复杂度却退化成了\(O(n)\)。
可以发现,当我们在追求一种操作的极致复杂度的同时,却总是造成另一种操作的复杂度严重退化。那么如果我们对于每种操作,都不要求最优的复杂度,而是各退一步追求共赢,有没有这样一种方法能够满足我们的需求呢?
当然有啦(不然我讲什么)
我们同时使用数组直接记录大小加上前缀和,但是两个我们都不做到极致,让两者并存。有人说,这怎么可能呢?
下面,就是见证奇迹的时刻
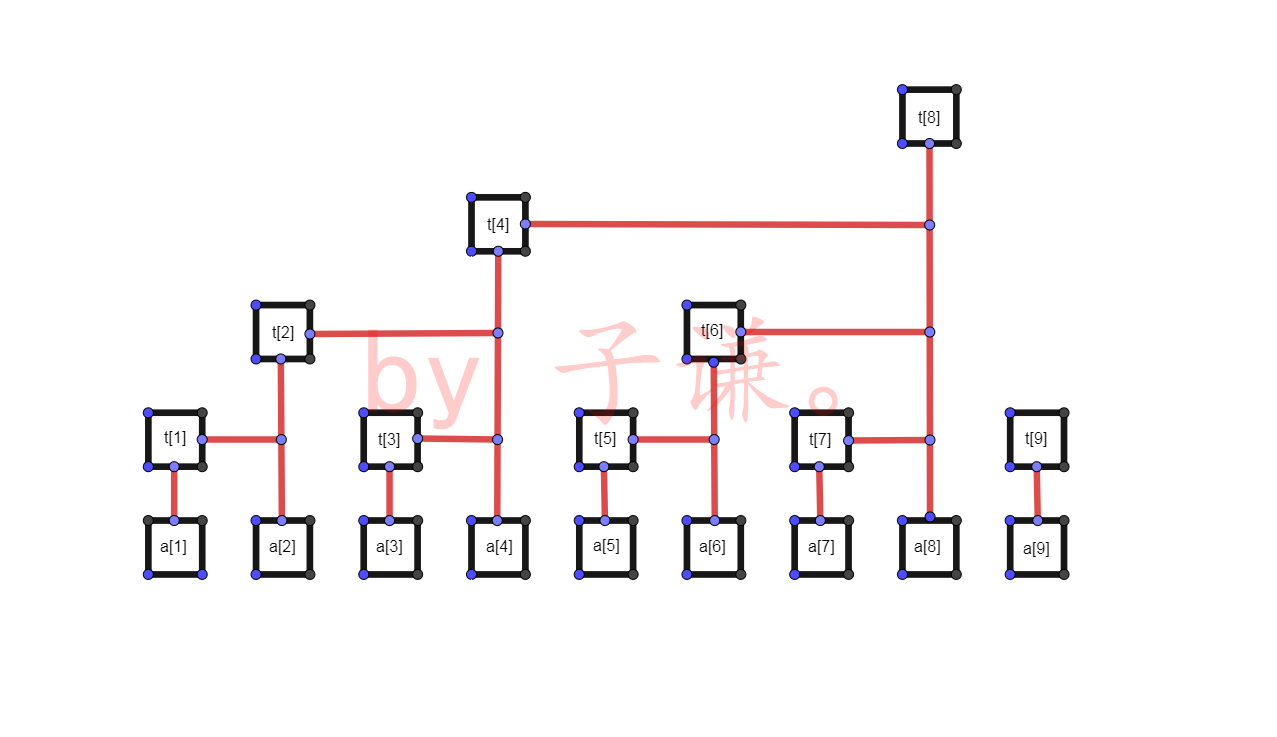
原始数组为\(a\)数组,我们把它存到\(t\)数组里,就像上面那样。我们会发现,这样存储非常的巧妙,我们把下标转换成二进制数就会发现,每一位存储了它和它前面总共(2的(二进制下它最后一个1后0的个数)次方)这么多个数的和(这句话很长,不太好理解,我用括号分割了一下,希望能易懂些)这里就体现出了我们之前所说的类似于前缀和的性质,而且很明显,它并不是传统意义上的前缀和,而是区间内的前缀和,而且不是连续的
这种奇怪的前缀和性质体现出来了,那么直接对数组进行加减的性质又是怎么体现的呢?
其实我们构建这个数组的时候,就相当于,初始每个数都是零,我们给第\(i\)个数加上\(a[i]\),就成了\(a\)数组的样子。那么怎么加呢?其实很简单,对于\(a[i]\)我们只需要把每个包含\(a[i]\)的位置加上对应的数即可。我们很容易想到,最高层的位置的二进制数一定是\(1\)后面全是\(0\),那么最多就有\(log_2 n\)层;我们又很容易发现,每个\(a[i]\)在\(t\)数组中的每一层最多出现一次,那么每次单点加至多会进行\(log_2 n\)次操作,区间求和同理,大家感性理解一下即可。
下面通过代码来感受一下吧
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cctype>
#define ll long long
#define gc getchar
#define maxn 500005
using namespace std;
inline ll read(){
ll a=0;int f=0;char p=gc();
while(!isdigit(p)){f|=p=='-';p=gc();}
while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=gc();}
return f?-a:a;
}int n,m;
ll tree[maxn];
#define lowbit(x) x&-x //lowbit操作表示找出最靠后的一个1
void add(ll a,int k){
while(k<=n){
tree[k]+=a;
k+=lowbit(k); //为什么要采用+lowbit的形式呢?大家可以自己思考一下,独立思考这个问题对加深对树状数组的理解意义非凡
}
}
ll query(int k){
ll ans=0;
while(k){
ans+=tree[k];
k-=lowbit(k); //为何是-,同上
}return ans;
}
inline void solve_1(){
int x=read();ll z=read();
add(z,x);
}
inline void solve_2(){ //区间求和求出的其实是前缀和,所以需要做一下减法
int x=read(),y=read();
printf("%lld\n",query(y)-query(x-1));
}
int main(){
n=read();m=read();
for(int i=1;i<=n;++i){
ll a=read();
add(a,i); //初始化的过程其实就是n次单点加的过程
}
while(m--){
int zz=read();
switch(zz){
case 1:solve_1();break;
case 2:solve_2();break;
}
}
return 0;
}
区间加,单点求和
如果把单点加换成区间加,区间求和换成单点求和又该怎么做呢?
其实几乎没有差别。
先引入一个概念——差分
差分
对于一个数组\(a\),我们对其进行如干次“对所有的\(a[i],i∈[x,y]\),加上\(w\)”的操作(下文中皆记作三元组“\((x,y,z)\)”),求最终的数组\(a\)
我们可以将其拆成两部分,一部分是原数组\(a\),一部分是操作产生的贡献。
我们用数组\(b\)来记录操作产生的贡献,那么对于操作"\((x,y,z)\)"我们将\(b[x]+=z,b[y+1]-=z\)来表示这次操作。当所有操作结束后,我们用\(c\)数组来表示\(b\)数组的前缀和,那么此时的\(c[i]\)的值,就是\(a[i]\)在这若干次操作中的变化量。
很神奇对吧,感性理解一下,其实并不难。
前缀和,差分
实际上这两种操作像是两种逆运算,一个数组的前缀和差分后就是原数组,一个数组被差分后求前缀和还是原数组。大家可以在平时的时间中多多注意这种现象,利用这种原理可以出很多有意思的题。
树状数组2
我们再回到这道题,当知道了差分是什么之后,是不是觉得一切都豁然开朗了。
没错,区间加操作就是对树状数组进行差分,而单点求和就是求树状数组的前缀和
下面直接看代码吧
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cctype>
#define ll long long
#define gc getchar
#define maxn 500005
using namespace std;
inline ll read(){
ll a=0;int f=0;char p=gc();
while(!isdigit(p)){f|=p=='-';p=gc();}
while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=gc();}
return f?-a:a;
}int n,m;
ll tree[maxn]; //整个树状数组的写法没有变化
#define lowbit(x) x&-x
void add(ll a,int k){
while(k<=n){
tree[k]+=a;
k+=lowbit(k);
}
}
ll query(int k){
ll ans=0;
while(k){
ans+=tree[k];
k-=lowbit(k);
}return ans;
}
inline void solve_1(){
int x=read(),y=read();ll z=read();
add(z,x);add(-z,y+1); //每次插入进行查分
}
inline void solve_2(){
int x=read();
printf("%lld\n",query(x)); //直接求前缀和求出的就是原数组变化后的值
}
int main(){
n=read();m=read();
for(int i=1;i<=n;++i){
ll a=read();
add(a,i);add(-a,i+1); //每次插入进行查分
}
while(m--){
int zz=read();
switch(zz){
case 1:solve_1();break;
case 2:solve_2();break;
}
}
return 0;
}
区间加,区间求和
对于这种操作,树状数组可以维护,但是代码量会迅速增长,这个时候,我们最好还是用因为常数问题被我们否决的线段树来处理,省时省力
单点加,单点求和
我推荐使用写\(LCT\),它是能够处理这个问题的最好写的数据结构
这个时候还是直接用数组来模拟吧,所有操作的复杂度都是\(O(1)\),没有必要再写什么数据结构来维护了
题目推荐
工作调度(极力推荐)(贪心题,我用离散化+树状数组+二分A掉了,来挑战下吧)
你理解树状数组了吗?这篇博客对你的学习是否有些许帮助呢?如果有的话,不妨点个推荐吧


