线段树入门详解+题目推荐

给出一个数组\(a\)，要求实现对数组进行两类操作：

第一类，给出区间\([x,y]\)，对区间内的每个\(a_i\)加上\(z\)/乘\(z\)等

第二类，给出区间\([x,y]\)，查询区间内所有元素的和/最大值/最小值等

最简单的方法，直接处理，每次处理复杂度\(O(n)\)，\(n\)次处理复杂度就是\(O(n^2)\)，如果\(n\)的范围扩大到\(1e5\)乃至\(1e6\)，这样的速度显然是我们无法承受的

还有没有什么更好的办法呢？

我们是否可以使用树状数组呢？对于区间加以及区间求和操作是可以的，但是写起来比较麻烦，今天我们用一种新方法来解决这个问题，那就是——

线段树！！

所谓线段树，顾名思义，就是由一条条线段组成的树。什么意思呢？我们来看图。

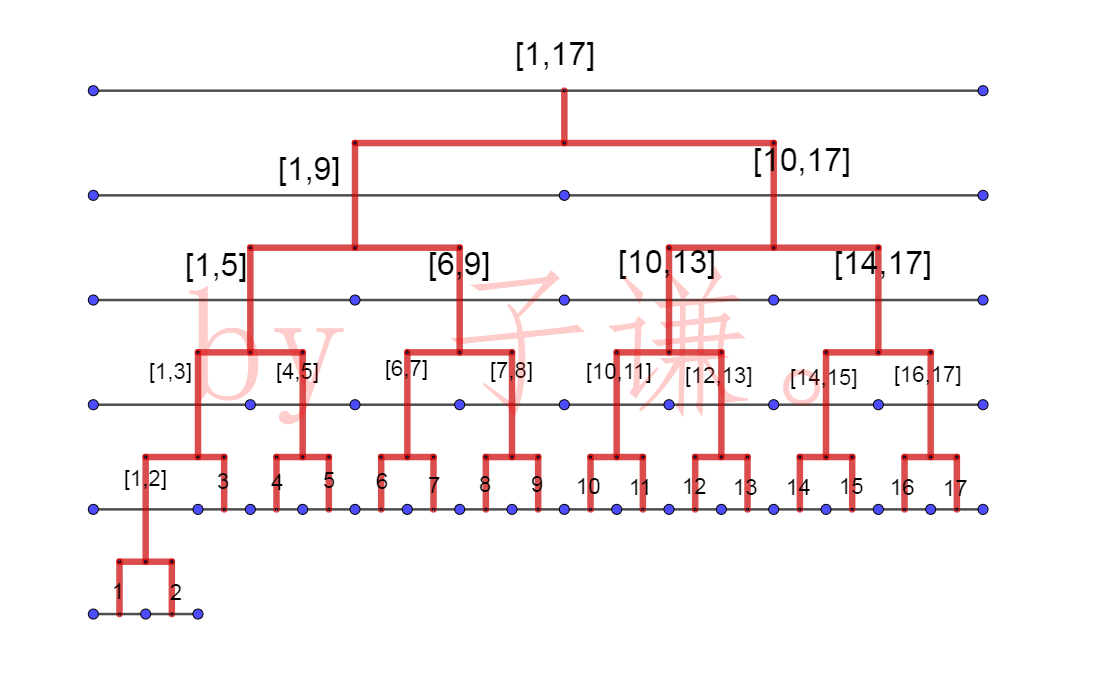
这个图从下往上看，我们发现最初的一个一个点不断地两两合并最终变成了一条长线段，而如果只注意红线的话，明显是一个二叉树结构，而且好像应该是一个完全二叉树

我们就可以利用一个这样的结构来存储区间和，当查询的时候只需要看当前区间是否属于查询区间，属于则返回这个区间的和，若是不属于，我们就查看它的左右区间，对于跟查询区间没有交集的区间我们可以直接返回，不需要继续向下搜索，这样的话复杂度最差是\(\lg n\)的（证明就省略了，大家也知道，我不擅长证明233）

那么这样的一棵树的创建我们应当如何通过代码来实现呢？复杂度：\(O(n)\)

void build(int p,int l,int r){ //p是当前节点的编号，l,r表示当前节点记录的是区间[l,r]的信息
	if(l==r){t[p]=a[l];return;}  //如果区间长度为1，那么就可以直接把数组的值存进来，然后返回
	int m=l+r>>1;  //这里的m是二分所用，看图应该也能明白
	build(lc,l,m);build(rc,m+1,r);  //这里的lc和rc代表的是p的左右子节点的编号，我们习惯于让p的左子节点编号为p的2倍，右子节点编号为p的2倍+1。这里的操作就是创建左右子树
	pushup(p);  //这个函数是用来根据左右子树来修改当前节点信息的函数，根据题目要求的不同，写法也不同，我们下面会提到，这里先把它当做一个可直接使用的系统自带函数即可
}

（短短的几行代码，浓缩了大量的精华，希望大家能够认真阅读我的注释，不然可能不好理解）

这棵树被创建好了，查询不成问题了，但是修改操作怎么办呢？如果按照创建的方法来修改，每次修改的复杂度都是\(O(n)\)，这就又成\(n^2\)算法了，费半天劲复杂度没变岂不是很亏。

所以我们用一种神奇的方法来进行区间修改操作。我们的修改操作大体与查询操作的思想是一样的，但是倘若不把修改进行到底，下次查询到这次修改区间的子区间，可能就会输出未修改的状态，这怎么办呢？

我们给每个节点做一个懒惰标记。为什么叫懒惰标记呢？因为它真的很懒惰，你踹它一脚它挪一步。当我们的修改操作进行到属于修改区间的区间的时候，我们把它的信息进行修改，然后用懒惰标记记录下来修改内容，然后返回。当后面进行修改操作或是查询操作访问到这个区间时，我们先将懒惰标记下放（也就是用懒惰标记修改其左右子节点的值，然后把懒惰标记传递给它的左右儿子，然后删除自己身上的懒惰标记）然后再继续进行之前要继续进行的操作。这样的话，每次修改的复杂度就从\(O(n)\)被优化成\(O(n\lg n)\)了

代码如下（以区间加区间求和为例）

void update(int p,int l,int r,int L,int R,int z){  //L,R表示的是要求修改的区间，z表示要求加上的数
	if(l>R||r<L)return;  //如果没有交集就直接退出，节约时间
	if(L<=l&&r<=R){t[p].v+=(r-l+1)*z;t[p].lz+=z;return;}  //如果属于修改区间就修改值，修改懒惰标记，返回
	int m=l+r>>1;if(t[p].lz)pushdown(p,l,r);  //pushdown操作是用来下放懒惰标记的函数，下面会提到，这里可以先当成一个系统自带的函数
	update(lc,l,m,L,R,z);update(rc,m+1,r,L,R,z);  //先修改左右子树
	pushup(p);  //根据左右子树修改后的值更新当前节点
}

知道了修改操作怎么写，其实查询操作就很简单了，直接放代码吧(还是以区间加区间求和为例)

int query(int p,int l,int r,int L,int R){  //如上
	if(l>R||r<L)return 0;
	if(L<=l&&r<=R)return t[p].v;  //如果当前区间属于查询区间，返回区间和
	int m=l+r>>1;if(t[p].lz)pushdown(p,l,r);  //下放懒惰标记
	return query(lc,l,m,L,R)+query(rc,m+1,r,L,R);  //不断查询左右子树
}

下面就该谈谈我们的\(pushup\)函数了。对于不同的需求写法也是不一样的，其实一般来说都很简单

inline void pushup(int p){  //区间求和
	t[p].v=t[lc].v+t[rc].v;
}
inline void pushup(int p){  //区间最值
	t[p].v=min(t[lc].v,t[rc].v);
}
inline void pushup(int p){  //区间积（这玩意一般用不上，因为太大一般需要取模，去膜后除法要变成逆元，比较麻烦）
	t[p].v=t[lc].v*t[rc].v;
}

相比于\(pushup\)函数，\(pushdown\)函数要麻烦许多

inline void pushdown(int p,int l,int r){  //区间加区间求和
	int m=l+r>>1,&lz=t[p].lz;
	t[lc].v+=(m-l+1)*lz;t[lc].lz+=lz;
	t[rc].v+=(r-m)*lz;t[rc].lz+=lz;
	lz=0;
}
inline void pushdown(int p,int l,int r){  //区间乘区间加区间求和
	int m=l+r>>1,&lz1=t[p].lz1,&lz2=t[p].lz2;
	if(t[p].lz1!=1){
		t[lc].v*=lz1,t[rc].v*=lz1;
		t[lc].lz1*=lz1,t[rc].lz1*=lz1;
		t[lc].lz2*=lz1,t[rc].lz2*=lz1;
		lz1=1;
	}
	if(t[p].lz2){
		t[lc].v+=(m-l+1)*lz2;t[lc].lz2+=lz2;
		t[rc].v+=(r-m)*lz2;t[rc].lz2+=lz2;
		lz2=0;
	}
}

线段树的各部分组成大家已经都看明白了，那么接下来就是把它连成一个整体

模板1

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cctype>
#define ll long long
#define gc getchar
#define maxn 100005
using namespace std;

inline ll read(){
	ll a=0;int f=0;char p=gc();
	while(!isdigit(p)){f|=p=='-';p=gc();}
	while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=gc();}
	return f?-a:a;
}int n,m;

struct ahaha{
	ll v,lz;
}t[maxn<<2];
#define lc p<<1
#define rc p<<1|1
inline void pushup(int p){
	t[p].v=t[lc].v+t[rc].v;
}
inline void pushdown(int p,int l,int r){
	int m=l+r>>1;ll &lz=t[p].lz;
	t[lc].v+=(m-l+1)*lz;t[lc].lz+=lz;
	t[rc].v+=(r-m)*lz;t[rc].lz+=lz;
	lz=0;
}
void build(int p,int l,int r){
	if(l==r){t[p].v=read();return;}
	int m=l+r>>1;
	build(lc,l,m);build(rc,m+1,r);
	pushup(p);
}
void update(int p,int l,int r,int L,int R,ll z){
	if(l>R||r<L)return;
	if(L<=l&&r<=R){t[p].v+=(r-l+1)*z;t[p].lz+=z;return;}
	int m=l+r>>1;if(t[p].lz)pushdown(p,l,r);
	update(lc,l,m,L,R,z);update(rc,m+1,r,L,R,z);
	pushup(p);
}
ll query(int p,int l,int r,int L,int R){
	if(l>R||r<L)return 0;
	if(L<=l&&r<=R)return t[p].v;
	int m=l+r>>1;if(t[p].lz)pushdown(p,l,r);
	return query(lc,l,m,L,R)+query(rc,m+1,r,L,R);
}

inline void solve_1(){
	int x=read(),y=read();ll z=read();
	update(1,1,n,x,y,z);
}
inline void solve_2(){
	int x=read(),y=read();
	printf("%lld\n",query(1,1,n,x,y));
}

int main(){
	n=read();m=read();
	build(1,1,n);
	while(m--){
		int zz=read();
		switch(zz){
			case 1:solve_1();break;
			case 2:solve_2();break;
		}
	}
	return 0;
}

模板2

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cctype>
#define ll long long
#define gc getchar
#define maxn 100005
using namespace std;

inline ll read(){
	ll a=0;int f=0;char p=gc();
	while(!isdigit(p)){f|=p=='-';p=gc();}
	while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=gc();}
	return f?-a:a;
}int n,m;ll mo;

struct ahaha{
	ll v,lz1=1,lz2;
}t[maxn<<2];
#define lc p<<1
#define rc p<<1|1
inline void pushup(int p){
	t[p].v=(t[lc].v+t[rc].v)%mo;
}
inline void pushdown(int p,int l,int r){
	int m=l+r>>1;ll &lz1=t[p].lz1,&lz2=t[p].lz2;
	if(lz1!=1){
		t[lc].lz2=t[lc].lz2*lz1%mo,t[rc].lz2=t[rc].lz2*lz1%mo;
		t[lc].lz1=t[lc].lz1*lz1%mo,t[rc].lz1=t[rc].lz1*lz1%mo;
		t[lc].v=t[lc].v*lz1%mo,t[rc].v=t[rc].v*lz1%mo;
		lz1=1;
	}
	if(lz2){
		t[lc].v=(t[lc].v+(m-l+1)*lz2)%mo,t[lc].lz2=(t[lc].lz2+lz2)%mo;
		t[rc].v=(t[rc].v+(r-m)*lz2)%mo,t[rc].lz2=(t[rc].lz2+lz2)%mo;
		lz2=0;
	}
}
void build(int p,int l,int r){
	if(l==r){t[p].v=read()%mo;return;}
	int m=l+r>>1;
	build(lc,l,m);build(rc,m+1,r);
	pushup(p);
}
void update1(int p,int l,int r,int L,int R,ll z){
	if(l>R||r<L)return;
	if(L<=l&&r<=R){
		t[p].lz1=t[p].lz1*z%mo;t[p].lz2=t[p].lz2*z%mo;
		t[p].v=t[p].v*z%mo;return;
	}
	int m=l+r>>1;pushdown(p,l,r);
	update1(lc,l,m,L,R,z);update1(rc,m+1,r,L,R,z);
	pushup(p);
}
void update2(int p,int l,int r,int L,int R,ll z){
	if(l>R||r<L)return;
	if(L<=l&&r<=R){t[p].lz2=(t[p].lz2+z)%mo;t[p].v=(t[p].v+(r-l+1)*z)%mo;return;}
	int m=l+r>>1;pushdown(p,l,r);
	update2(lc,l,m,L,R,z);update2(rc,m+1,r,L,R,z);
	pushup(p);
}
ll query(int p,int l,int r,int L,int R){
	if(l>R||r<L)return 0;
	if(L<=l&&r<=R)return t[p].v;
	int m=l+r>>1;pushdown(p,l,r);
	return (query(lc,l,m,L,R)+query(rc,m+1,r,L,R))%mo;
}

inline void solve_1(){
	int x=read(),y=read();ll z=read();
	update1(1,1,n,x,y,z);
}
inline void solve_2(){
	int x=read(),y=read();ll z=read();
	update2(1,1,n,x,y,z);
}
inline void solve_3(){
	int x=read(),y=read();
	printf("%lld\n",query(1,1,n,x,y));
}

int main(){
	n=read();m=read();mo=read();
	build(1,1,n);
	while(m--){
		int zz=read();
		switch(zz){
			case 1:solve_1();break;
			case 2:solve_2();break;
			case 3:solve_3();break;
		}
	}
	return 0;
}

题目推荐

你理解线段树了吗？如果这篇博客能够给你些许帮助的话，不妨点个推荐吧

posted @ 2019-09-21 21:15 子谦。阅读(417) 评论(0) 编辑收藏举报

刷新页面返回顶部

子谦。

愿得忘忧水千觞，尽饮却愁再轻狂

线段树入门详解+题目推荐

题目推荐

公告