P4254 [JSOI2008]Blue Mary开公司
这道题的意思就是给出若干个一次函数,当\(x=x_0\)时,最大的\(y\)为多少
这种题可以用李超线段树来处理
什么是李超线段树呢?
李超线段树存储的是在区间上方暴露最多的直线标号,为了便于描述,我们称它为优势直线
例如下图
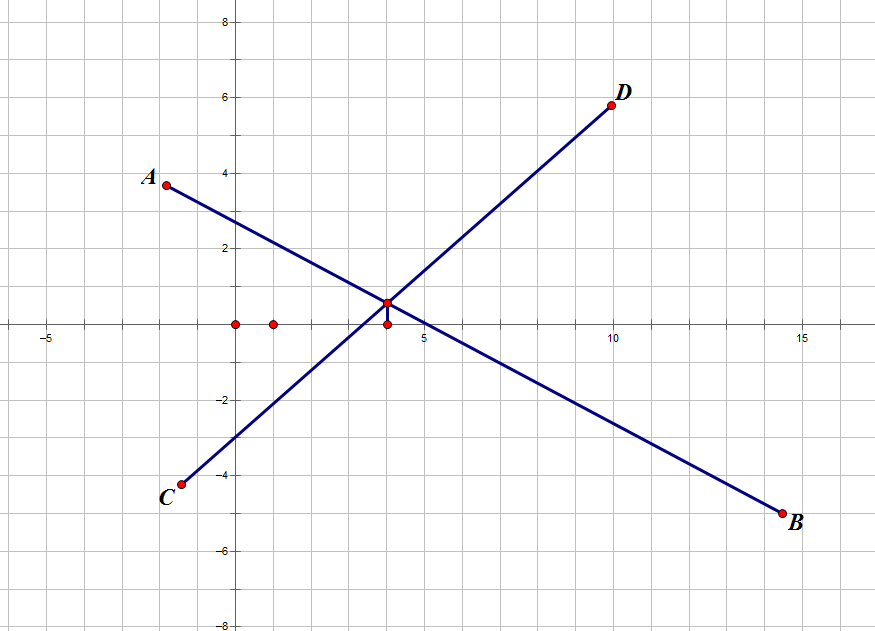
在区间[0,5],AB就是暴露最多的线段
可以证明,当\(x=x_0\)时最大的\(y\),一定属于所有包含\(x_0\)的区间的优势直线
那么我们怎么存储呢?
对于区间[l,r],如果没有优势直线,那么直接把当前直线改为它的优势直线
如果有优势直线,如果当前直线完全在优势直线上方,那么把当前直线视为优势直线
如果完全在优势直线下方,那么直接返回即可
如果以上情况都不是,那么说明在当前区间两条直线各有优劣
那么我们比较在中点处哪条直线更靠上,将其改为当前区间的优势直线,另一条直线下放到子区间,它的优势范围在左侧就下放到左子区间,反之下放到右子区间
查询的时候对于每一层都去max即可
下面放这道题的代码
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cctype>
#include<cmath>
#define db double
#define ll long long
#define gc getchar
#define maxn 100005
#define maxm 50005
using namespace std;
inline ll read(){
ll a=0;int f=0;char p=gc();
while(!isdigit(p)){f|=p=='-';p=gc();}
while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=gc();}
return f?-a:a;
}int n;
db a[maxn],b[maxn];
db F(int p,int x){
return a[p]+b[p]*(x-1);
}
int t[maxm<<2];
#define lc p<<1
#define rc p<<1|1
void update(int p,int l,int r,int L,int R,int z){
if(l>R||r<L)return;
int m=l+r>>1;
db lz=F(z,l),rz=F(z,r),lv=F(t[p],l),rv=F(t[p],r);
if(lz>=lv&&rz>=rv){t[p]=z;return;}
if(lz<=lv&&rz<=rv)return;
int l1=t[p],l2=z;db mv=F(l1,m),mz=F(l2,m);
if(mz>mv)t[p]=z,swap(l1,l2);
if(b[l1]>b[l2])update(lc,l,m,L,R,l2);
else update(rc,m+1,r,L,R,l2);
}
db query(int p,int l,int r,int k){
if(l==r)return F(t[p],k);
int m=l+r>>1;db ans=F(t[p],k);
if(k<=m)return max(ans,query(lc,l,m,k));
else return max(ans,query(rc,m+1,r,k));
}
int tot;
inline void solve_1(){++tot;
scanf("%lf%lf",&a[tot],&b[tot]);
update(1,1,50000,1,50000,tot);
}
inline void solve_2(){
int k=read();
printf("%d\n",(int)query(1,1,50000,k)/100);
}
char s[10];
int main(){
n=read();
while(n--){
scanf("%s",s+1);
switch(s[1]){
case 'P':solve_1();break;
case 'Q':solve_2();break;
}
}
return 0;
}
所有文字著作权归本人所有,禁止转载抄袭,若盗版进行商业运营,本人必将追究到底。


