逻辑回归问题（Logistic Regression）

　　逻辑回归算法是分类算法，它适合于标签 y 取值离散的情况

假说表示

　　在分类的问题中，我们需要什么样的函数来表示我们的假设，例如我们在做分类的时候，希望我们的分类器的输出值在0~1之间，因此，我们希望满足某个性质的假设函数，这个性质是该函数的预测值在 0~1之间。

　　

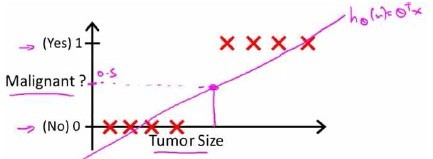
 　　例如上图给出的乳腺癌分类问题，我们希望可以用线性回归的方法求出适合数据的一条直线，但由于线性回归模型只能预测连续的值，但是对于二分类问题，我们只需要输出 0 或 1 ，所以我们可以定义：

　　

 

 

 　　对于上图所示的数据，线性回归似乎能很好的完成分类问题。但是，假设我么你现在又观测到一个非常大尺寸的恶性肿瘤，将其作为一条直线加入到我们的训练集中来，则我们会得到一条新的直线，这时候在使用 0.5 作为阈值似乎并不合理，并且线性回归模型的值可以超过 [ 0，1 ] 的范围，所以线性回归模型并不符合。

 

　　因此，我们引入一个新的模型。逻辑回归模型，该模型的输出范围始终在 0~1 之间。逻辑回归模型的假设为：

 

 

 

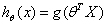
　　其中 X 代表特征向量 ，g 代表逻辑函数，其公式为：

 

 

　　该函数的图像为：

 

 

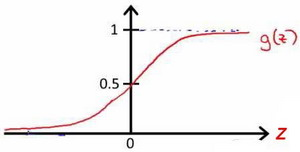
 　　对于逻辑回归模型 h_Θ(x) 的理解为，给定输入的变量，根据选择的参数计算输出变量等于 “ 1 ” 的可能，即：

 

　　例如：，则说明有 70% 的可能 y 为正类。

决策边界

 

 　　

 

 　　在逻辑回归预测中：

 

　　并且根据图像我们可以看出：

 

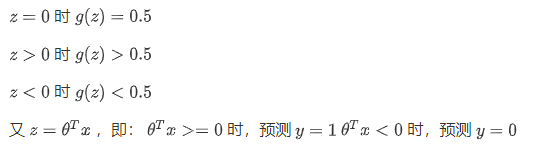
 　　现在我们有一个模型：

 

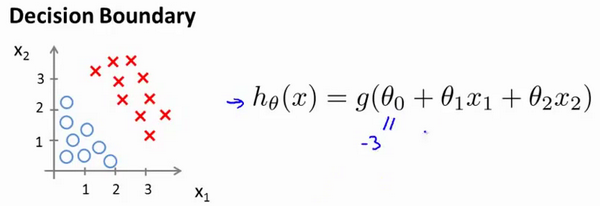
 　　并且参数Θ为 [ -3,1,1 ] 时 ，则当：　-3 + x₁+x₂ >= 0 时，模型将预测 y=1，所以，我们可以绘制  x₁+x₂ = 3 这条直线作为我们的分界线

　　

 

　　但是当数据是这个样子的时候，怎样选择模型？

　　

 

 　　则我们需要曲线方程来进行区分，例如：

　　

 

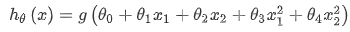
　　即我们可以用非常复杂的模型来适应形状非常复杂的判定边界。