OI学习笔记2:计算几何(凸包与旋转卡壳)
计算几何(凸包与旋转卡壳)
一、二维向量
1、定义。
- 二维向量是二维平面中的有向线段。
- \(\vec{a}=(x,y)\) 表示从 \((0,0)\) 运动到 \((x,y)\)。
- 向量的模:向量长度,记为 \(|\vec{a}|\)。
2、向量运算。
- 单位向量:三维空间中,\(\vec{i}=(1,0,0),\vec{j}=(0,1,0),\vec{k}=(0,0,1)\),则三维空间中任一向量 \(\vec{a}\) 均唯一可被表示为 \(\vec{i},\vec{j},\vec{k}\) 的线性组合。即 \(\vec{a}=x\vec{i} +y\vec{j} +z\vec{k}\)。此时 \(\vec{i},\vec{j},\vec{k}\) 张成 \(R^3\),为 \(R^3\) 的单位向量(标准基)。
(1)向量加法。
- 对于向量 \(\vec{a}=(x_a,y_a),\vec{b}=(x_b,y_b)\),有 \(\vec{a}+\vec{b}=(x_a+x_b,y_a+y_b)\)。
- 对于减法而言,将上述式子中加号换成减号即可。
(2) 向量积。
- 点积(标量积,内积)
- 定义:两向量水平分量的乘积。
- 几何定义式:\(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\)。
- 代数定义式:\(\vec{a} \cdot \vec{b}=x_ax_b +y_ay_b\)。
- 线性代数定义式:\(\vec{a}^T \vec{b}=\begin{bmatrix}x_1 & x_2\end{bmatrix} \begin{bmatrix}y_1\\y_2\end{bmatrix}=x_1y_1 +x_2y_2\)。
- 更一般地,有 \(n\) 维向量点积:\(\vec{a} \cdot \vec{b}=\sum_{i=1}^{n}a_ib_i\)。
- 点积有分配律,但因为它的结果是标量,所以点积没有方向。
- 叉积(矢量积,外积)
- 定义:两向量垂直分量的乘积。叉积的结果是向量,所以有方向。
- 几何定义式:\(\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin \theta\)。注意:该式子只能求出叉积的模,不能得到方向。
- 代数定义式:三维空间中,设 \(\vec{a}=(x_a,y_a,z_a),\vec{b}=(x_b,y_b,z_b)\),\(则\vec{a} \times \vec{b}=det\begin{vmatrix}\vec{i} & \vec{j} & \vec{k} \\ x_a & y_a & z_a \\ x_b & y_b & z_b \end{vmatrix}=(y_az_b-z_ay_b)\vec{i} + (x_az_b-z_ax_b)\vec{j} +(x_ay_b-x_by_a)\vec{k}\)
- 代数定义式二维情况下,\(\vec{a} \times \vec{b}=(x_ay_b-x_by_a)\vec{k}\)。
- 线性代数定义式(外积展开):\(\vec{a} \times \vec{b}=\begin{bmatrix} x_a \\ y_a \\ z_a \end{bmatrix} \begin{bmatrix}x_b & y_b & z_b \end{bmatrix}=\begin{bmatrix} x_ax_b & x_ay_b & x_az_b \\ y_ax_b & y_ay_b & y_az_b \\ z_ax_b & z_ay_b & z_az_b \end{bmatrix}\)。
- 右手法则:\(\vec{a} \times \vec{b}\) 时,右手由 \(\vec{a}\) 握向 \(\vec{b}\),大拇指方向为叉积方向。
- 叉积可快速计算由相邻向量形成的平行四边形面积。
- 应用:
- 判断向量位置关系(见凸包)。
二、凸包
1、二维凸包。
(1)定义。
- 凸多边形:所有内角大小都在 \([0,\pi]\) 范围内的简单多边形。
- 凸包:平面上能包含所有给定点的最小凸多边形。
(2)构建方法。
- 找到一个必定在凸包上的点,然后按顺时针或逆时针顺序依次加入所有点
- 1、极角序,Graham扫描法。
- 算法流程:
- 找到纵坐标最小的点,该点必在凸包上。
- 将该点设为原点,剩下的点用叉积进行极角排序。
- 用单调栈维护,若两向量叉积 \(\geq 0\),则另一个向量不在凸包上。
- 主要函数实现:
- 向量结构体:
struct Vector{ double x, y; Vector(const double &x, const double &y){ this->x = x; this->y = y; } Vector(){} void read(){ scanf("%lf%lf", &x, &y); } double length(){ return sqrt(x * x + y * y); } } Vector a[N], s[N];//N由题目确定,a数组存储给定点,s数组存储凸包上的点。 Vector operator - (const Vector &a, const Vector &b){ return Vector(a.x - b.x, a.y - b.y); }- 叉积函数:
double cross(Vector a, Vector b){ return a.x * b.y - a.y * b.x; }- 极角序计算函数:(这里使用相对距离计算极角序,精确度更高)
double dis(Vector a, Vector b){ Vector c = a - b; return c.length(); }- 极角序比较函数:
int cmp(Vector p, Vector q){ double x = cross(p - a[1], q - a[1]); if(x > 0) return 1; if(x == 0 && dis(p, a[1]) < dis(q, a[1])) return 1; return 0; }- 叉积判断向量位置关系:(左正右负)
double multi(Vector a, Vector b, Vector c){ return cross(b - a, c - a); }- 主函数核心部分:
int main(){//n为给定点的个数 ....... int k = 1; for(int i = 2; i <= n; i++) if(a[i].y < a[k].y || (a[k].y == a[i].y && a[i].x < a[k].x)) k = i; swap(a[1], a[k]);//得出原点。 sort(a + 2, a + 1 + n, cmp); s[1] = a[1]; s[2] = a[2]; int t = 2; for(int i = 3; i <= n; i++){ while(t >= 2 && multi(s[t - 1], s[t], a[i]) <= 0) t--;//题目要求凸包上的点可共线时取等号,否则不取。 s[++t] = a[i]; } ....... }
- 算法流程:
- 2、水平序,Andrew算法
- 算法流程:
- 以 \(x\) 为第一关键字,\(y\) 为第二关键字排序,排序后,最小与最大元素必在凸包上。
- 最大与最小元素连线处切开分上下凸壳扫描。
- 算法流程:
- 判断点是否在凸包内。
- 以凸包最下面的点为原点。
- 变换坐标。
- 找到与该点极角最接近的两点形成的线段,用叉积来判定。
(3)例题
- 例题1:城墙
一个贪婪的国王要求他的建筑师建一堵墙围绕他的城堡,且墙与城堡之间的距离总不小于一个数 \(L\) 。输入城堡各个节点(图中实线与实线的交点)的坐标和 \(L\) ,要求最小的墙壁周长。
输入格式:
输入第一行 \(N(3\leq N \leq 1000)\)和 \(L(1\leq L \leq 1000)\),其中 \(N\) 为节点个数。以下 \(N\) 行每行是各个节点的横坐标 \(x_i\) 和纵坐标 \(y_i\) ,其中 \(-10^4\leq x_i,y_i \leq 10^4\)。
输出格式:
输出仅一个数,为最小的墙壁周长(四舍五入至整数)。
输入样例:
9 100
200 400
300 400
300 300
400 300
400 400
500 400
500 200
350 200
200 200
输出样例:
1628
这道题的核心是墙与城堡之间的距离总不小于一个数 \(L\) 。但是几何这玩意有难想象,所以这时候就要发挥 \(OIer\) 的传统手艺(画图)了!
随便画了个图出来,圆弧部分距离每个点的距离均为 \(L\),仔细观察一下红线圈出来的区域,有什么发现?
这些圆弧拼起来恰巧是一个圆,不信的同志可以自己画来算,很简单的。
再仔(随)细(便)观(一)察(猜),发现每一条直线就是两个点间的距离,所以问题就转化成了:求凸包周长,求出来后再加上一个圆的周长就OK了,妥妥的模板题了。
//AC代码,压行严重,勿喷。
#include<bits/stdc++.h>
using namespace std;
const double PI = acos(-1.0);
int n, L;
struct point{
double x, y;
point(const double &x, const double &y){ this->x = x; this->y = y; }
point(){}
void read(){ scanf("%lf%lf", &x, &y); }
double length(){ return sqrt(x * x + y * y); }
}a[1005], s[1005];
point operator - (const point &a, const point &b){return point(a.x - b.x, a.y - b.y);}
double X(point a, point b){ return a.x * b.y - a.y * b.x; }
double dis(point a, point b){ point c = a - b; return c.length(); }
int cmp(point p, point q){
double x = X( p - a[1], q - a[1] );
if(x > 0) return 1;
if(x == 0 && dis(p, a[1]) < dis(q, a[1])) return 1;
return 0;
}
double multi(point a, point b, point c){ return X(b - a, c - a); }
int Round(double x){
int r;
if(x - (int)x > 0.5)r = (int)x + 1;
else r = (int)x;
return r;
}
int main(){
scanf("%d%d", &n, &L);
for(int i = 1; i <= n; i++) a[i].read();
int k = 1;
for(int i = 2; i <= n; i++) if(a[i].y < a[k].y || (a[k].y == a[i].y && a[i].x < a[k].x)) k = i;
swap(a[1], a[k]);
sort(a + 2, a + 1 + n, cmp);
s[1] = a[1];
s[2] = a[2];
int t = 2;
for(int i = 3; i <= n; i++){
while(t >= 2 && multi(s[t - 1], s[t], a[i]) <= 0) t--;
s[++t] = a[i];
}
// cout<<endl;
// for(int i = 1; i <= t; i++)cout<<s[i].x<<" "<<s[i].y<<endl;
double sum = 0;
for(int i = 1; i < t; i++) {
sum += dis(s[i], s[i + 1]);
}
sum += dis(s[1], s[t]) + PI * L * 2;
cout<<Round(sum);
return 0;
}
- 例题2:信用卡凸包(SHOI2012)
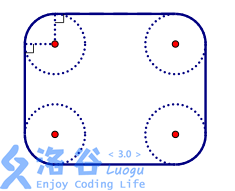
信用卡是一个矩形,唯四个角作了圆滑处理,使它们都是与矩形的两边相切的 1/4 圆,如下图所示。现在平面上有一些规格相同的信用卡,试求其凸包的周长。注意凸包未必是多边形,因为它可能包含若干段圆弧。
输入格式:
输入的第一行是一个正整数 \(n\),表示信用卡的张数。第二行包含三个实数 \(a,b,r\),分别表示信用卡(圆滑处理前)竖直方向的长度、水平方向的长度,以及 \(\frac{1}{4}\) 圆的半径。
之后 \(n\) 行,每行包含三个实数 \(x,y,\theta\),分别表示一张信用卡中心(即对角线交点)的横、纵坐标,以及绕中心 逆时针旋转的 弧度。
输出格式:
输出只有一行,包含一个实数,表示凸包的周长,四舍五入精确到小数点后2位。
输入样例1:
2
6.0 2.0 0.0
0.0 0.0 0.0
2.0 -2.0 1.5707963268
输出样例1:
21.66输入样例2:
3
6.0 6.0 1.0
4.0 4.0 0.0
0.0 8.0 0.0
0.0 0.0 0.0
输出样例2:
41.60输入样例3:
3
6.0 6.0 1.0
4.0 4.0 0.1745329252
0.0 8.0 0.3490658504
0.0 0.0 0.5235987756
输出样例3:
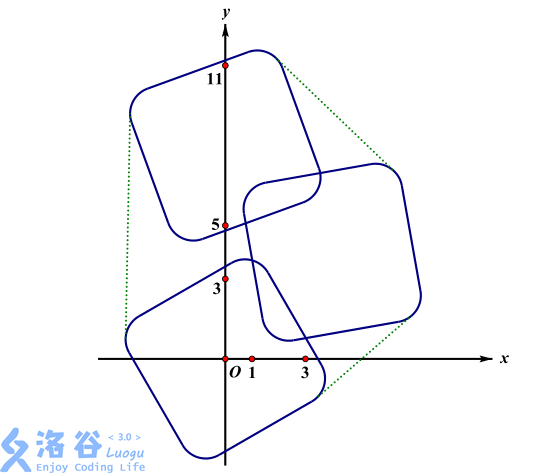
41.63样例3说明:
分析:
- 考虑 \(r = 0\) 的情况,发现此时信用卡就是矩形,所以跑一遍Graham算法就可以了。
- 考虑 \(r \geq 1\) 的情况,经过多次传统手艺(画图)分析,发现在多张信用卡形成的带圆弧的凸包上,圆弧所对应的圆心角之和总为 \(2\pi\)。适用我们只需要跑一遍Graham再加上一个整圆的周长就可以了。这个规律与例题1相同。
- 设当前点为 \(A(x,y)\),则它绕原点逆时针旋转 \(\theta\) 后的坐标为 \(A′(xcos\theta −ysin\theta ,xsin\theta +ycos\theta )\)。
有了这些,这个题目就成了一个裸的凸包模板。
//AC代码
#include<bits/stdc++.h>
#define MAXN 10005
using namespace std;
const double PI = 3.141592653589793;
const double eps = 1e-23;
int n, t1;
double A, B, R;
struct point{
double x, y;
point(const double &x, const double &y){ this->x = x; this->y = y; }
point(){}
double length(){ return sqrt(x * x + y * y); }
}a[MAXN<<2], s[MAXN<<2];
bool operator == (const point &a, const point &b){
if(a.x == b.x && a.y == b.y) return true;
return false;
}
point operator + (const point &a, const point &b){ return point(a.x + b.x, a.y + b.y); }
point operator - (const point &a, const point &b){ return point(a.x - b.x, a.y - b.y); }
double X(point a, point b){ return a.x * b.y - a.y * b.x; }
double dis(point a, point b){ point c = a - b; return c.length(); }
double multi(point a, point b, point c){ return X(b - a, c - a); }
int cmp(point p, point q){
double x = X(p - a[1], q - a[1]);
if(x > 0) return 1;
if(x == 0 && dis(p, a[1]) < dis(q, a[1])) return 1;
return 0;
}
point rotate(double x, double y, double t){
double c = cos(t), s = sin(t);
return point( x * c - y * s, x * s + y * c );
}
double Round(double x){
double r;
if(x - floor(x) - 0.99 > 0.005)r = x - floor(x) + 0.01 + (int)x;
else r = x;
return x;
}
int main(){
scanf("%d", &n);
scanf("%lf%lf%lf", &A, &B, &R);
A/=2, B/=2;
double cir = PI * 2.0 * R;
for(int i = 1; i <= n; i++){
double x, y, rou;
scanf("%lf%lf%lf", &x, &y, &rou);
x+=eps; y += eps; rou += eps;
point pp = point(x, y);
a[++t1] = rotate(B - R, A - R, rou) + pp;
a[++t1] = rotate(-B + R, A - R, rou) + pp;
a[++t1] = rotate(B - R, -A + R, rou) + pp;
a[++t1] = rotate(-B + R, -A + R, rou) + pp;
}
int k = 1;
for(int i = 1; i <= t1; i++) if(a[i].y < a[k].y || (a[i].x < a[k].x && a[i].y == a[k].y)) k = i;
swap(a[k], a[1]);
sort(a + 2, a + 1 + t1, cmp);
s[1] = a[1];
int cnt = 1;
for(int i = 2; i <= t1; i++){
while(cnt > 1 && multi(s[cnt - 1], s[cnt], a[i]) <= 0) cnt--;
s[++cnt] = a[i];
}
s[++cnt] = a[1];
double sum = 0;
for(int i = 1; i < cnt; i++)sum += dis(s[i], s[i + 1]);
printf("%.2lf", Round(sum + cir));
return 0;
}
2、动态凸包。
- 使用平衡树进行动态插入与排序
- 主要思路:快速定位凸包需要调整的部分,然后进行调整。
- 为统一排序标准,将凸包分为上下凸壳。
- 上凸壳关于 \(x\) 轴对称后就变为下凸壳,方便操作。
- 水平序,极角序均可。
- 插入一个点时,判断是否在凸包下方。
- 如果是,则插入且不断往两边删点,直到所有点都满足凸包定义为止。
- 注意边界处的点不要同时加入上下凸包。
- 为统一排序标准,将凸包分为上下凸壳。
- 每个点只会加入和弹出平衡树一次,所以时间复杂度为 \(O(N\log^2N)\)
- 动态凸包不支持删除。
- 离线后倒序处理,将删除转为加点。
- 主要思路:快速定位凸包需要调整的部分,然后进行调整。
- 线段树分治:建立凸包时,按照归并思想合并左右子树凸包,避免重新排序。
- \(CDQ\) 分治
- 二进制分组 \(\&\) 定期重构
- 缺点:不支持删除操作。
三、旋转卡壳
1、前置知识。
(1)凸多边形的直径。
- 定义:一个凸多边形上任意两点距离的最大值为凸多边形的直径。
- 确定直径的点可能多于一对
- 一个凸 \(N\) 边形可能存在 \(n\) 对直径。
(2)支撑线。
- 直线 \(L\) 过凸多边形 \(P\) 一个顶点,使 \(P\) 全在 \(L\) 一侧,此时称直线 \(L\) 为凸多边形 \(P\) 的支撑线。
(3)对踵点。
- 两条平行直线过凸多边形的两个顶点且将凸多边形夹在其之间,此时这对顶点称作对踵点。
- 两条平行支撑线所过两点是一对对踵点。
- 一个凸 \(N\) 边形的对踵点最多有 \(\left \lceil \frac{3N}{2} \right \rceil\) 对。
(4)凸多边形直径定理。
- 凸多边形 \(P\) 的直径 \(=\) 凸多边形 \(P\) 的所有平行支撑线之间距离的最大值。
- 凸多边形的直径可在对踵点对中寻找。
2、旋转卡壳算法。
(1)旋转卡壳:寻找凸多边形对踵点的算法。
- 主要思路:利用凸包单调性,枚举点 -> 更新点对 -> 更新答案。
- 算法流程:
- 求出凸多边形凸包。此时最远点对必在凸包上,时间复杂度为 \(O(N\log N)\)。
- 找到一对初始对踵点,作水平切线。
- 选 \(y_{max}\) 与 \(y_{min}\)。
- 更新答案。
- 沿一个方向旋转这两条切线,知道其中一条与凸包的边重叠。
- 产生新对踵点对,更新答案。
- 不断重复这一过程,直到所有点对都已生成对踵点。
- 该算法本质上是对于每一条凸包的边,计算最远的过凸包上点的平行直线。
- 两直线距离可看作三角形面积除以底边,用叉积计算。
- 代码中心:
int rotating_calipers(){ int re = 0; if(t == 2) return dis(s[1], s[2]); int j = 2; for(int i = 1; i <=t; i++){ while(multi(s[i], s[i % t + 1], s[j]) <= multi(s[i], s[i % t + 1], s[j % t + 1])) j = j % t+1; re = max(re, max(dis(s[i], s[j]), dis(s[i % t+ 1], s[j]))); } return re;//返回的是凸多边形直径。 }
(2)例题
给定平面上 \(n\) 个点,求凸包直径。
输入格式:
第一行一个正整数 \(n\)。
接下来 \(n\) 行,每行两个整数 \(x,y\),表示一个点的坐标。
输出格式:
输出一行一个整数,表示答案的平方。
输入样例:
4
0 0
0 1
1 1
1 0
输出样例:
2
说明/提示:
【数据范围】
对于 \(100\%\) 的数据,\(2\leq n \leq 50000,|x|,|y|\leq 10^4\)。
简单的模板题,直接上程序。
//AC代码
#include<bits/stdc++.h>
#define MAXN 50005
using namespace std;
int n, t;
struct point{
int x, y;
point(int x, int y):x(x), y(y){}
point(){}
void read(){ scanf("%d%d", &x, &y); }
int length(){ return x * x + y * y; }
}a[MAXN], s[MAXN];
point operator - (const point &a, const point &b){
return point(a.x - b.x, a.y - b.y);
}
int X(point a, point b){
return a.x * b.y - a.y * b.x;
}
int multi(point a, point b, point c){ return X(b - a, c - a); }
int dis(point a, point b){
point c = a - b;
return c.length();
}
int cmp(point p, point q){
int x = X(p - a[1], q - a[1]);
if(x > 0) return 1;
if(x == 0 && dis(p, a[1]) < dis(q, a[1])) return 1;
return 0;
}
void convex_hull(){
int k = 1;
for(int i = 1; i <= n; i++)
if(a[i].y < a[k].y || (a[i].y == a[k].y && a[i].x < a[k].x))
k = i;
swap(a[1], a[k]);
sort(a + 2, a + 1 + n, cmp);
s[1] = a[1];
t = 1;
for(int i = 2; i <= n; i++){
while(t > 1 && multi(s[t - 1], s[t], a[i]) <= 0)
t--;
s[++t] = a[i];
}
}
int rotating_calipers(){
int re = 0;
if(t == 2) return dis(s[1], s[2]);
int j = 2;
for(int i = 1; i <=t; i++){
while(multi(s[i], s[i % t + 1], s[j]) <= multi(s[i], s[i % t + 1], s[j % t + 1]))
j = j % t+1;
re = max(re, max(dis(s[i], s[j]), dis(s[i % t+ 1], s[j])));
}
return re;
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++) a[i].read();
convex_hull();
printf("%d", rotating_calipers());
return 0;
}
(3)应用。
- 凸多边形直径与宽。
- 凸多边形间距离。
- 凸多边形最小面积/周长外接矩形。
- 定理:关于凸多边形 \(P\) 的一个外接矩形与 \(P\) 的一边重合。