许多程序员认为浮点数没意思，往坏了说，深奥难懂。我们将看到，因为IEEE 格式是定义在一组小而一致的原则上的，所以它实际上是相当优雅和容易理解的。
首先来看一段代码，请问下描代码输出结果是( ).
#include <stdlib.h> #include <stdio.h> #define LOOP 1000000 #define NUM 500 #define DATA 0.000061 int main() { float *pf = malloc(NUM * sizeof(float)); for (int i = 0; i < NUM; ++i) pf[i] = DATA; float res = 0.0; for (int j = 0; j < LOOP; ++j) for (int i = 0; i < NUM; ++i) res += pf[i]; printf("%f\n", res); return 0; }
A. 30500 (0.000061 * 500 * 1000000)
B. 与A同量级的近似值
C. 具体值不知道, 但肯定是小于A量级某个浮点数
D. 1024.0 (精确值)
相信大部分人答案都是B，说明对浮点有一定了解，但是没有很深入，正确答案是D，很诧异吧！下面我们来深入梳理下这个问题！
一、二进制小数
理解浮点数的第一步是考虑含有小数值的二进制数字。首先，让我们来看看更熟悉的十进制表示法。十进制表示法使用如下形式的表示：
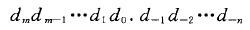
其中每个十进制数4 的取值范围是0 9。这个表达描述的数值d 定义如下：
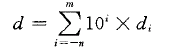
数字权的定义与十进制小数点符号(".") 相关，这意味着小数点左边的数字的权是10的正幂，得到整数值，而小数点右边的数字的权是10 的负幂，得到小数值。例如:
12.34。表示数字1x10^1 + 2x10^0 + 3x10^-1 + 4x10^-2 = 12.34。 类推到二进制，一个形如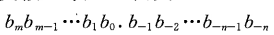
的二进制值，其中每个二进制数字，或者称为位，bi的取值范围是0和1，如下图所示，
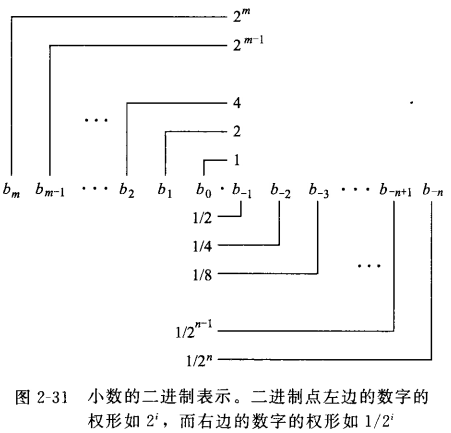
这种表示的数b定义如下：
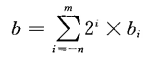
符号“.”现在变成了二进制的点，点左边的位权是2的正幂，点右边的位的权是2的负幂。例如101.11表示的值为：1x2^2 + 0x2^1 + 1x2^0 + 1x2^-1 + 1x2^-2 = 4+0+1+1/2+1/4 = 23/4。
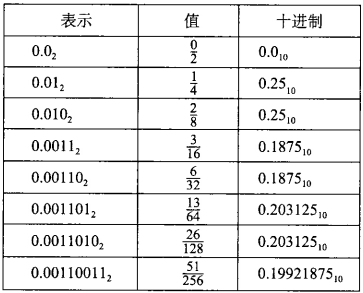
假定我们仅考虑有限长度的编码， 那么十进制表示法不能准确地表达像1/3和5/7这样的分数。 类似， 小数的二进制表示法只能表示那些能够被写成x*2^y的数。其他的值只能够被近似地表示。
例如， 数字1/5可以用十进制小数 0.20 精确表示。 不过， 我们并不能把它准确地表示为一个二进制小数， 我们只能近似地表示它， 增加二进制表示的长度可以提高表示的精度，如下图所示，随着位数增加，值越趋接近0.20。
二、IEEE浮点表示
第一章中谈到的定点表示法有明显的缺点，不能有效的表示非常大的数字。例如，数字5x2^100需要用二进制101后面跟100个0的位模式来表示，效率低下。相反，我们希望通过给定的x和y值，来表示形如x*2^y的数值。
IEEE浮点标准用V=(-1)^s * M * 2^E的形式来表示一个浮点数：
a、符号位(sign)：s决定了这数是负数(s=1)还是正数(s=0)，而对于数值0的符号位解释作为特殊情况处理。
b、尾数(significand)：M是一个二进制小数，他的范围是1~2-ε，或者是0~1-ε。(2-ε表示无限接近2，1-ε表示无限接近1)
c、阶码(exponent)：E的作用是对浮点数加权，这个权重是2的E次幂，E可能是负数。
由上述可知，IEEE标准将浮点数的位划分成了3个字段来表示，三个字段单独编码：
a、一个单独的符号位s，直接编码；
b、k个比特位的阶码字段exp，用来编码阶码E；
c、n个比特位的小数字段 frac 编码尾数M；
如下图所示，单精度(float)中，s、exp和frac字段分别固定位1bit、k=8bit和n=23bit，一共32bit；双精度(double)中，s、exp和frac字段分别固定位1bit、k=11bit和n=52bit，一共64bit。
根据exp的值不同，被编码的值可以分成三种不同的情况，分别为：
1、规格化的；
2、非规格化的；
3、无穷大、NAN；
我们这边只讨论常规的规格化的数值表示，这是最普遍的情况。
当exp的各个位既不全为0，也不全为1（单精度位255，双精度为2047）时，都属于这类情况。在这种情况下，阶码字段被解释为以偏置(biased)形式表示的有符号整数。为什么要引入偏置呢？主要原因是为了让阶码可以表示负幂，这样可以表示更小的小数。也就是说，阶码字段的实际值：E=e - Bias，其中e是无符号数，就是exp字段的字面二进制值，而Bias是个固定的偏置值：Bias=2^(k-1) - 1;（k表示exp字段的比特数目，float时Bias=127，double是1023）。由于引入了偏置，所以阶码E的取值范围变为：-126~+127(float)，-1022~+1023(double)。
小数字段 frac 被解释为描述小数值f， 其中 0<= f <1， 其二进制表示为 0.f(n-1)...f1f0，也就是二进制小数点在最高有效位的左边。尾数定义为 M=1 + f。 有时，这种方式也叫做隐含的以 1 开头的（implied leading 1 )表示 ， 因为我们可以把 M 看成一个二进制表达式为 1.f(n-1)...f1f0的数字。既然我们总是能够调整阶码E，使得尾数 M 在范围 1<=M<2 之中（E增加，M就会相应减小），那么这种表示方法是一种轻松获得一个额外精度位的技巧。既然第一位总是等于 1，那么我们就不需要显式地表示它。
我们通过几个例子来实际理解下IEEE浮点数的计算方法，我们以float类型为例子：
例1、十进制数值是0.125，求对应的float存储内容。
i)、0.125首先转换为V=(-1)^s * M * 2^E的形式，需要保证M处于1~2-ε之间，可以得到：0.125 = 1.0 * 1/8 = (-1)^0 * 1.0 * 2^-3。
ii)、可以得到flaot表达式的各个值，s=0， M=1.0，E=-3。进而得到阶码字段e = E+Bias = -3 + 127 = 124；尾数：f = M - 1 = 1.0 - 1 = 0；
iii)、通过s=0，e=124，f=0，得到float对应的二进制数为：0 0111 1100 0000 0000 0000 0000 0000 000
例2、十进制数值是4.5，求对应的float存储内容。
i)、4.5 首先转换为V=(-1)^s * M * 2^E的形式，需要保证M处于1~2-ε之间，可以得到：4.5 = 1.125 * 4 = (-1)^0 * 1.125 * 2^2。
iii)、可以得到flaot表达式的各个值，s=0， M=1.125，E=2。进而得到阶码字段e = E+Bias = 2 + 127 = 129；尾数：f = M - 1 = 1.125 - 1 = 0.125；
iv)、通过s=0，e=129，f=0.125，得到float对应的二进制数为：0 1000 0001 0010 0000 0000 0000 0000 000
我们通过一段C程序运行下验算是否正确，代码如下：
#include <stdio.h> #include <stdlib.h> char *printfloat(float f, char *str) { int offset = 0; int bitcnt = 0; unsigned int *pui = (unsigned int *)&f; while(bitcnt < 32) { if (*pui & (0x80000000 >> bitcnt)) str[offset++] = '1'; else str[offset++] = '0'; if (bitcnt%4 == 0) str[offset++] = ' '; bitcnt++; } str[offset] = '\0'; return str; } int main(void) { float a = 0.125; float b = 4.5; char s[50]; printf("a=%f, [%s]\n", a, printfloat(a, s)); printf("b=%f, [%s]\n", b, printfloat(b, s)); return 0; }
代码运行结果如下图所示，可以发现和演算的是一致的。
三、浮点加减运算
前面两章我们深入理解了浮点数格式，目前为止并没有涉及到开篇题目的问题点。不急，量变导致质变，基础知识是良好的地基。从第二章的浮点数表示方法可以看出来，其限制了浮点数的范围和精度，所以浮点运算只能近似地表示实数运算。
由于浮点数的数值： V=(-1)^s * M * 2^E， 所以当有两个浮点数加/减操作时，相当于是两个等式计算，不能直接使用二进制位操作。
例如，f1 = (-1)^s1 * M1 * 2^E1， f2 = (-1)^s2 * M2 * 2^E2，求f1+f2？显然，必须等通过变换，使f1、f2式子中有三个变量只有一个不同是，运用乘法结合律才能求值，这个变换就就是对阶，对阶目的就是使两浮点数 E 相同，
浮点数的加减运算过程如下图所示：
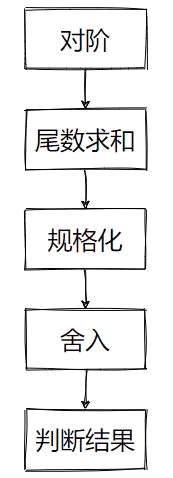
①、对阶：是两数的小数点位置对齐，小阶码转换为大阶码。就是f1和f2的E要相同，因为E+1，相应的M2*2^-1，等式结果还是不变的。
②、尾数求和：将对阶后的两浮点数的尾数M做加减运算求和（差）；
③、舍入：为提高精度，要考虑尾数右移时丢失的数值位；
④、判断结果：判断结果是否溢出；
例3：float a = 1.00001; float b = 100.0；求a+b?
根据第二章所述：
a = 1.00001 = (-1)^0 * 1.00001 * 2^0; 得到s=0， f = M-1 = 0.00001，e = E + 127 = 0 + 127 = 127；
二进制原码表示：由于float的尾数精度=1/(2^23) ≈ 0.00000011920928955078125；所以不能精确的表示0.00001（不能整除），f = 0.00001/(1/2^23) ≈ 84 = 0101 0100
所以a = 0 0111 1111 0000 0000 0000 0000 1010 100
b = 100.0 = (-1)^0 * 1.5625 * 2^6;得到s=0， f = M-1 = 0.5625，e = 6 + 127 = 133；
二进制原码表示： 0 1000 0101 1001 0000 0000 0000 0000 000
1、由于a、b两数的阶码E不同，所以需要先对阶，对齐到较大的b的阶码，从0->6;
对于a，e = 6 + 127 = 133，对应的需要将M右移6位；变换后，a = 0 1000 0101 0000 0100 0000 0000 0000 001，可以看到对阶后a的尾数发生了损失，同时右移需要带上尾数M的个位1；
2、对阶后可以对a和b求值了，由于都是正数，相当于是尾数M直接相加；
M = 0000 0100 0000 0000 0000 001 + 1001 0000 0000 0000 0000 000 = 1001 0100 0000 0000 0000 001
带上符合位s和阶码e：0 1000 0101 1001 0100 0000 0000 0000 001 = 0x42CA0001 = 101.00000762939453125 ≈ 101.000008
运行结果如下所示：
#include <stdio.h> #include <stdlib.h> int main(void) { float a = 1.00001; float b = 100.0; printf("a+b=%f\n", a+b); return 0; }
可以看到a+b结果并不是等于101.0001，由于对阶过程的精度损失，实际结果等于101.000008！
四、答案解析
同理，回顾开篇的试题，本题考察的知识点就是浮点数运算中对阶过程的精度损失问题。分析代码运行，res会从0+0.000061。。。程序将经历如下阶段：
①、res逐步累加，每次增加0.000061；
②、由于res足够大，导致运算时0.000061的尾数需要做右移，以符合与res的对阶要求，此时res每次累加小于0.000061；
③、随着res进一步加大，测试0.000061由于对阶，全部实际尾数变成了0，测试res每次实际累加0，大小不变。
那res要多大值时，才能达到第三阶段呢？这个取决于每次累加的大小，本题中=0.000061；
0.000061 = (-1)^0 * 2^0 * (0.000061) = (-1)^0 * 2^0 * (1000000000)；可以看出，当阶码E=0时，尾数M=512=1000000000；所以当res足够大，需要M右移10位对阶时，此时M损失掉数值，M=0；
所以，可以得到第③阶段时，res的阶码E=10；此时res = (-1)^0 * 2^10 * (1.0) = 1024.0
参考：
1、https://www.cnblogs.com/Five100Miles/p/13171185.html
2、IEEE754：http://kfe.fjfi.cvut.cz/~klimo/nm/ieee754.pdf
3、《深入理解计算机系统》
