JPEG编码协议--DCT变换

      从之前的几篇文章介绍可以看出，JPEG编码最重要的一步就是DCT变换，将空域的图像信号转换到频域，达到良好的去空间相关性的性能，DCT变换本身是无损的。因此DCT变换在图像编码领域被广泛应用。

一、一维DCT变换

      在JPEG编码中使用了二维DCT变换，一维DCT是二维的基础，我们先看下一维DCT变换。一维DCT变换共有8种形式，其中最常用的是第二种形式，由于其运算简单、适用范围广。我们在这里只讨论这种形式，其表达式如下：

    其中，f(i)为原始的信号，F(u)是DCT变换后的系数，N为原始信号的点数，c(u)可以认为是一个补偿系数，可以使DCT变换矩阵为正交矩阵。对应的逆DCT变换公式为：

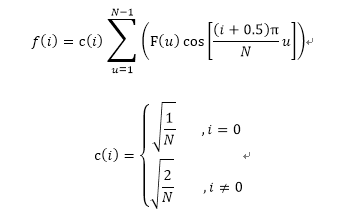
二、二维DCT变换

    二维DCT变换其实是在一维DCT变换的基础上再做了一次DCT变换，其公式如下：

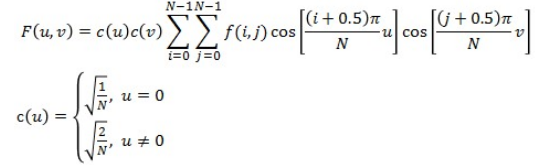
     f(i, j)为原始像素的信号，F(u, v)是DCT变换后对应点位的系数，N为原始信号的点数，c(u)/c(v)可以认为是一个补偿系数。

    由公式我们可以看出，上面只讨论了二维图像数据为方阵的情况，在实际应用中，如果不是方阵的数据一般都是补齐之后再做变换的，重构之后可以去掉补齐的部分，得到原始的图像信息，这个尝试一下，应该比较容易理解。

    如果原始信号是图像等相关性较大的数据的时候，我们可以发现在变换之后，系数较大的集中在左上角，而右下角的几乎都是0，其中左上角的是低频分量，右下角的是高频分量，低频系数体现的是图像中目标的轮廓和灰度分布特性，高频系数体现的是目标形状的细节信息。DCT变换之后，能量主要集中在低频分量处，这也是DCT变换去相关性的一个体现。

      之后在量化和编码阶段，我们可以采用“Z”字形编码，这样就可以得到大量的连续的0，这大大简化了编码的过程。

 三、二维DCT反变换

     在图像的接收端，根据DCT变化的可逆性，我们可以通过二维DCT反变换恢复出原始的图像信息，其公式如下：

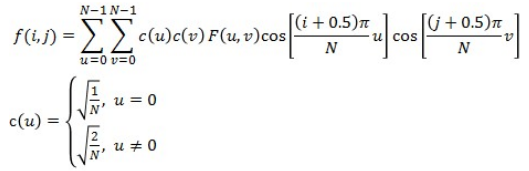
 四、分块DCT变换

    在实际的图像处理中，DCT变换的复杂度其实是比较高的，所以通常的做法是，将图像进行分块，然后在每一块中对图像进行DCT变换和反变换，在合并分块，从而提升变换的效率。具体的分块过程中，随着子块的变大，算法复杂度急速上升，但是采用较大的分块会明显减少图像分块效应，所以，这里面需要做一个折中，在JPEG编码中，采用8*8的分块。

 五、代码分析

     从《JPEG编码协议--代码实现》中，我们可以看到代码上对DCT实现的部分，我们再次来分析这块代码：

void _forword_FDCT(const float* channel_data, float* fdct_data)
{
    const float PI = 3.1415926f;
    for(int v=0; v<8; v++)
    {
        for(int u=0; u<8; u++)
        {
            float alpha_u = (u==0) ? 1/sqrt(8.0f) : 0.5f;
            float alpha_v = (v==0) ? 1/sqrt(8.0f) : 0.5f;

            float temp = 0.f;
            for(int x=0; x<8; x++)
            {
                for(int y=0; y<8; y++)
                {
                    float data = channel_data[y*8+x];

                    data *= cos((2*x+1)*u*PI/16.0f);
                    data *= cos((2*y+1)*v*PI/16.0f);

                    temp += data;
                }
            }
            temp = alpha_u*alpha_v*temp;
            fdct_data[v*8+u] = temp;
        }
    }
}

     在上述的变换实现中，通过for循环实现了8x8的变换块。

     1、第4行和第6行变换后的系数，可以看到此处是8x8变换，会得到8x8个DCT系数；

     2、第8行和第9行求出公式中c(u)和c(v)的值；

     3、第12行和第14行的for循环，对8x8的像素数据做变换。对应公式中的累加部分；

     4、第16行对应为f(i, j)值；

     5、第18/19行，分别求值公式中的两个cos函数；

     6、第21行完成一次累加，完成12~23行循环，结束全部累加；

     7、第24行累加结果和c(u)、c(v)相乘，得到f(u, v)位置的DCT系数；

     8、重复2~7步骤，得到8x8变换块每个位置的系数。

     相应的，我们可以根据公式，得到反变换IDCT的代码实现：

void _forword_IDCT(const float* fdct_data, float* channel_data)
{
    const float PI = 3.1415926f;
    for(int i=0; i<8; i++)
    {
        for(int j=0; j<8; j++)
        {
            float cos_i = (2*i+1)*PI/16.0f;
            float cos_j = (2*j+1)*PI/16.0f;

            float temp = 0.f;
            for(int u=0; u<8; u++)
            {
                for(int v=0; v<8; v++)
                {
                    float alpha_u = (u==0) ? 1/sqrt(8.0f) : 0.5f;
                    float alpha_v = (v==0) ? 1/sqrt(8.0f) : 0.5f;                
                    float data = alpha_u*alpha_v*fdct_data[u*8+v]*cos(cos_i*u)*cos(cos_j*v);
     
                    temp += data;
                }
            }
            channel_data[i*8+j] = temp;
        }
    }
}

     IDCT变换的代码和FDCT差异不大，结合第三节公式即可看懂；

六、demo测试

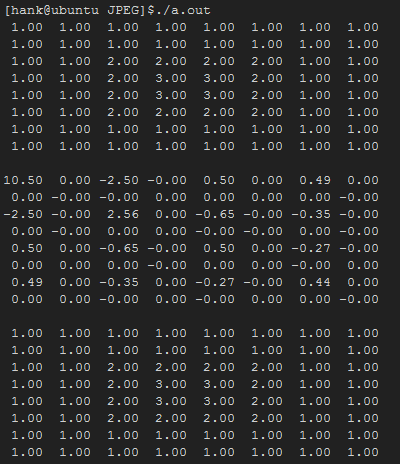
    我们通过如下demo来测试公式，代码首先构造8x8数据块，首先做FDCT变换，得到变换系数，之后通过IDCT反变换得到原始数据块。

#include <stdio.h>
#include <math.h>

void _forword_FDCT(const float* channel_data, float* fdct_data)
{
    const float PI = 3.1415926f;
    for(int v=0; v<8; v++)
    {
        for(int u=0; u<8; u++)
        {
            float alpha_u = (u==0) ? 1/sqrt(8.0f) : 0.5f;
            float alpha_v = (v==0) ? 1/sqrt(8.0f) : 0.5f;

            float temp = 0.f;
            for(int x=0; x<8; x++)
            {
                for(int y=0; y<8; y++)
                {
                    float data = channel_data[y*8+x];

                    data *= cos((2*x+1)*u*PI/16.0f);
                    data *= cos((2*y+1)*v*PI/16.0f);

                    temp += data;
                }
            }
            temp = alpha_u*alpha_v*temp;
            fdct_data[v*8+u] = temp;
        }
    }
}

void _forword_IDCT(const float* fdct_data, float* channel_data)
{
    const float PI = 3.1415926f;
    for(int i=0; i<8; i++)
    {
        for(int j=0; j<8; j++)
        {
            float cos_i = (2*i+1)*PI/16.0f;
            float cos_j = (2*j+1)*PI/16.0f;

            float temp = 0.f;
            for(int u=0; u<8; u++)
            {
                for(int v=0; v<8; v++)
                {
                    float alpha_u = (u==0) ? 1/sqrt(8.0f) : 0.5f;
                    float alpha_v = (v==0) ? 1/sqrt(8.0f) : 0.5f;                
                    float data = alpha_u*alpha_v*fdct_data[u*8+v]*cos(cos_i*u)*cos(cos_j*v);
     
                    temp += data;
                }
            }
            channel_data[i*8+j] = temp;
        }
    }
}

#define PRINTF_BLOCK(p)    do{  \
                                for(int i=0; i<8; i++) \
                                {                        \
                                    for(int j=0; j<8; j++) \
                                        printf("%5.2f ", p[i*8+j]); \
                                    printf("\n");  \
                                }  \
                                printf("\n");\
                            }while(0);
int main(int argc, char *argv[])
{
    float data[64] = {
        1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 2, 2, 2, 2, 1, 1,
        1, 1, 2, 3, 3, 2, 1, 1,
        1, 1, 2, 3, 3, 2, 1, 1,
        1, 1, 2, 2, 2, 2, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1,
        1, 1, 1, 1, 1, 1, 1, 1
    };
    float fdct_data[64];
    PRINTF_BLOCK(data);
    _forword_FDCT(data, fdct_data);
    PRINTF_BLOCK(fdct_data);
    _forword_IDCT(fdct_data, data);
    PRINTF_BLOCK(data);
    return 0;
}

     运行结果如下，可以看到经过FDCT变换后，数据复杂度明显降低，且IDCT后可以完整的还原原始数据。