在H.265的编码语法参数解析中，语法元素描述符等于ue(v)或se(v)时，表示使用指数哥伦布编码。编码为ue表示为无符号指数哥伦布编码，编码为se表示有符号指数哥伦布编码。
如下表所示，给出了指数哥伦布编码的码字结构，该结构将二进制比特流串分为了“前缀”和“后缀”两个部分。其中，“前缀”通过计算0bit的数量，计算得到leadingZeroBits的值，在表中通过0或者1表示；“后缀”通过得到的leadZeroBits，使用特定公式计算得出，“后缀”部分在表中以xi表示。
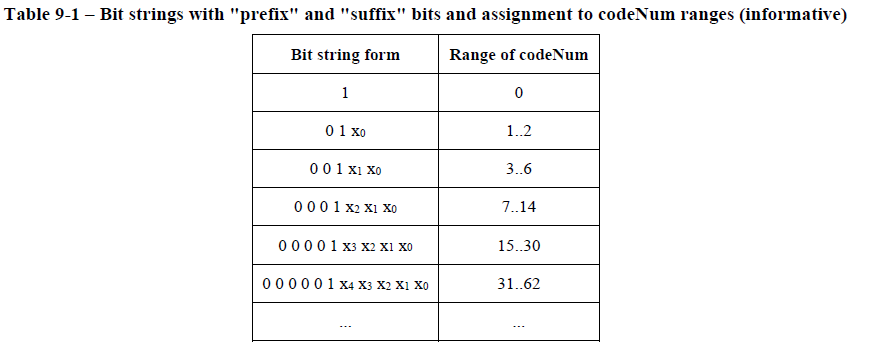
下表列举了部分ue(n)编码比特流对应的解析后码字；
下面来看具体的解析过程：
1、计算前缀leadingZeroBits:
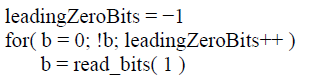
2、计算后缀，得到码字
通过计算方法可以得知，指数哥伦布编码通过前缀0的数目，指定了后缀码字所占用的比特长度，同时使用前缀数目值作为指数值来编码码字。
当编码描述为se(v)时，语法元素表示为有符号数，语法元素按照绝对值的升序排序，负值按照其绝对值参与排序，排在正值后面，如下表所示：
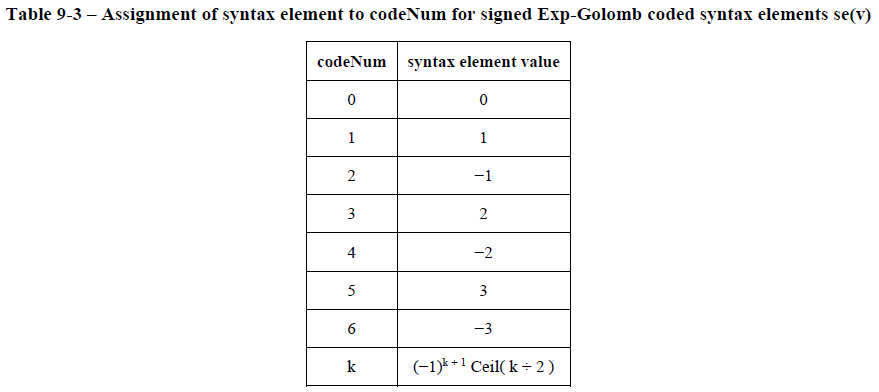
具体的参数解析C代码如下：
1 static int held_bits_num; 2 static int held_bits; 3 int read_bits(uint8_t **pp, int bitnum) 4 { 5 uint8_t *pByte = *pp; 6 int code = 0; 7 int aligend = 0; 8 int next_held_bits_num; 9 10 if (bitnum < held_bits_num) //bitnum小于前一次读取剩余bit，直接返回 11 { 12 code = held_bits >> (held_bits_num - bitnum); 13 code &= ~(0xff << bitnum); 14 held_bits_num -= bitnum; 15 return code; 16 } 17 18 //bitnum大于前一次读取剩余bit，先读取剩余，不足bit再取新Byte 19 bitnum -= held_bits_num; 20 code = held_bits & ~(0xff << held_bits_num); 21 code <<= bitnum; 22 23 switch((bitnum-1)>>3) 24 {//利用switch读取1~4字节数据 25 case 3: aligend = (*pByte++) << 24; 26 case 2: aligend |= (*pByte++) << 16; 27 case 1: aligend |= (*pByte++) << 8; 28 case 0: aligend |= (*pByte++); 29 } 30 next_held_bits_num = (32-bitnum) % 8; 31 code |= aligend >> next_held_bits_num; 32 33 held_bits_num = next_held_bits_num; //存储剩余可读bits 34 held_bits = aligend; 35 36 *pp = pByte; //更新sps地址 37 38 return code; 39 } 40 41 int read_bits_ue(uint8_t **pp) 42 { 43 int ZeroBits = -1; 44 int code; 45 int bitval; 46 for (bitval = 0; !bitval; ZeroBits++) 47 bitval = read_bits(pp, 1); 48 code = (1 << ZeroBits)-1 + read_bits(pp, ZeroBits); 49 50 return code; 51 } 52 53 int read_bits_se(uint8_t **pp) 54 { 55 int k = read_bits_ue(pp); 56 57 return ((int)pow(-1, k+1)) * ((int)ceil(k/2.0)); 58 }
