Perlin Noise
原理
Perlin Noise属于晶格(grid) 噪声,其将空间分成一个个晶格(单位长度),输入的位置点配合晶格顶点处的随机梯度,生成噪声。常用于游戏中的地形生成等。
以二维Perlin Noise为例
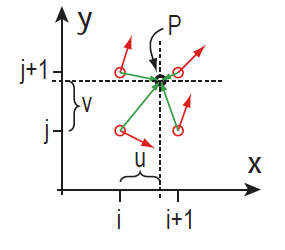
P是输入点,周围四个红色圈代表其所在晶格的四个顶点。(u, v)是p点在这个晶格内的局部坐标(u,v范围在0~1),红色向量代表晶格顶点处的随机梯度向量,绿色向量代表四个顶点到输入点的距离向量。
接着通过这两个向量的点乘得到该顶点对P点的影响权重,四个顶点对应四个权重,w1, w2, w3, w4。
w1----------w2
| |
| |
w3----------w4
再对4个权重做插值,插值函数可以直接用线性函数 w1*(1-u)+w2*u,但实际上会选用更复杂的插值函数保证一阶和二阶导数的连续性:
x1=Lerp(w1, w2, u);
x2=Lerp(w3, w4, u);
y1=Lerp(x1, x2, v);
这里需要做3次插值(2次水平方向,1次竖直方向)。以上就是全部流程,通过输入一个二维坐标,输出一个浮点噪声值。
还有一个问题是如何得到一个顶点的随机梯度向量,其实应该说伪随机梯度向量,因为算法中同一个顶点每次生成的梯度是相同的。
Perlin使用的方法是预先生成一组伪随机梯度值,对二三维来说是梯度向量,保存在G[256](一维),G2[256][2](二维),G3[256][3](三维)中。对于一维情况可以直接根据顶点坐标去G中取值,对二三维情况需要一个数组Q,将0~255下标随机放在其中。对于输入的顶点坐标这样取值:
以上就完成了随机取梯度值的方法。Perlin在这里有一个改进,在三维中,P点周围的最近8个点构成了一个立方体,P点到立方体的每条边的的向量有12个,柏林使用这12个随机梯度向量替代了原先的256个梯度向量。

也就是从上面12个向量中挑一个。
实现

上面实现中,Fade()方法是插值函数,它保证了一二阶导数的连续性。permutation[256]保存了0~255的随机排列。
效果




