数据结构（三）树、二叉树、最优二叉树

树

　　树形结构是一类非常重要的非线性结构，它可以很好地描述客观世界中广泛存在的具有分支关系或层次特性的对象，因此在计算机领域里有着广泛应用，如操作系统中的文件管理、编译程序中的语法结构和数据库系统信息组织形式等。

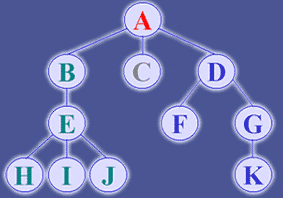
树的相关定义

节点的度：一个节点含有的子树的个数称为该节点的度；
树的度：一棵树中，最大的节点的度称为树的度；
叶节点或终端节点：度为零的节点；
非终端节点或分支节点：度不为零的节点；
双亲节点或父节点：若一个结点含有子节点，则这个节点称为其子节点的父节点；
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
兄弟节点：具有相同父节点的节点互称为兄弟节点；
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次；
堂兄弟节点：双亲在同一层的节点互为堂兄弟；
节点的祖先：从根到该节点所经分支上的所有节点；
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
森林：由m（m>=0）棵互不相交的树的集合称为森林；

二叉树

　　二叉树是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树的形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。

　　二叉树(BinaryTree)是n(n≥0)个结点的有限集，它或者是空集(n=0)，或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。

　　完全二叉树：对于一颗二叉树，假设其深度为d（d>1）。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树。

1.二叉树的遍历

　　所谓遍历二叉树，就是遵从某种次序，访问二叉树中的所有结点，使得每个结点仅被访问一次。

　　二叉树的遍历包括三种：

DLR称为前根遍历(前序遍历)
- 　　访问结点的操作发生在遍历其左右子树之前
LDR称为中根遍历(中序遍历)
- 　　访问结点的操作发生在遍历其左右子树之中(间)
LRD称为后根遍历(后序遍历)

　　访问结点的操作发生在遍历其左右子树之后

递归实现：

void preorder(NODE *p)
{
if(p!=NULL)
{printf(“%d ”,p->data);
preorder(p->lchild);
preorder (p->rchild);}
}
 
void InOrder(BinTree T)
{
     if(T) { // 如果二叉树非空 
      InOrder(T->lchild)；
      printf("％c"，T->data)； // 访问结点 
     InOrder(T->rchild);
    }
} // InOrder 
 
void posorder(NODE *p)
{
   if(p!=NULL)
   {
       posorder(p->lchild);
       posorder (p->rchild);
       printf(“%d ”,p->data);
    }
｝

非递归实现：

/*算法思想：
 
利用队列基本操作
1.初始化：根结点入队列
2.while(队列非空)
{
a.队首元素出队列
b.原队首元素对应的左、右孩子(非空)入队列
}*/ 
 
void traverse(NODE *T)
{
   NODE *q[100];
   int head,tail, i;
   q[0]=T;head=0;tail=1;
   while(head<tail)
   {
      p=q[head++];
      printf(“%c”,T->data);
      if(p->lchild!=NULL)
         q[tail++]=p->lchild;
      if(p->rchild!=NULL)
         q[tail++]=p->rchild;
     }
}

2.二叉树的构造

　　基于先序遍历的构造，即以二叉树的先序序列为输入构造。

void CreateBinTree (BinTree *T)
{
        char ch；
        if((ch=getchar())=='')
               *T=NULL； //读人空格，将相应指针置空  
        else{ //读人非空格 
              *T=(BinTNode *)malloc(sizeof(BinTNode))； //生成结点 
              (*T)->data=ch；
              CreateBinTree(&(*T)->lchild)； //构造左子树 
              CreateBinTree(&(*T)->rchild)； //构造右子树 
         }
 }

最优二叉树

　在权为w_l，w₂，…，w_n的n个叶子所构成的所有二叉树中，带权路径长度最小(即代价最小)的二叉树称为最优二叉树或哈夫曼树。

　　假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：

将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；
在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
从森林中删除选取的两棵树，并将新树加入森林；
重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

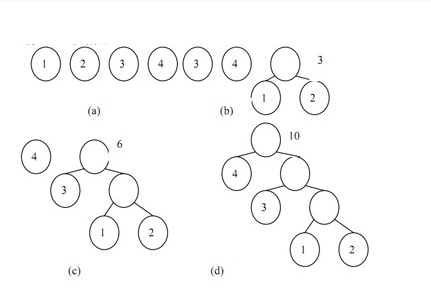
　　具体代码：

#include "stdio.h" 
#include "stdlib.h" 
#define m 100
 
struct ptree              //定义二叉树结点类型 
{
int w;                   //定义结点权值 
struct ptree *lchild;     //定义左子结点指针 
struct ptree *rchild;     //定义右子结点指针 
};
 
struct pforest              //定义链表结点类型 
{
struct pforest *link;
struct ptree *root;
};
 
int WPL=0;                  //初始化WTL为0 
struct ptree *hafm();
void travel();
struct pforest *inforest(struct pforest *f,struct ptree *t);
 
void travel(struct ptree *head,int n)                     
{
//为验证harfm算法的正确性进行的遍历 
struct ptree *p;
p=head;
if(p!=NULL)
 {
       if((p->lchild)==NULL && (p->rchild)==NULL) //如果是叶子结点 
      {
              printf("%d ",p->w);
              printf("the hops of the node is: %d/n",n);
       WPL=WPL+n*(p->w);    //计算权值 
         }//if 
travel(p->lchild,n+1);
travel(p->rchild,n+1);
}//if 
}//travel 
 
struct ptree *hafm(int n, int w[m])
{
struct pforest *p1,*p2,*f;
struct ptree *ti,*t,*t1,*t2;
int i;
f=(pforest *)malloc(sizeof(pforest));
f->link=NULL;
for(i=1;i<=n;i++)          //产生n棵只有根结点的二叉树 
  {
       ti=(ptree*)malloc(sizeof(ptree));//开辟新的结点空间 
    ti->w=w[i];               //给结点赋权值 
    ti->lchild=NULL;
    ti->rchild=NULL;
    f=inforest(f, ti);
       //按权值从小到大的顺序将结点从上到下地挂在一颗树上       
  }//for 
while(((f->link)->link)!=NULL)//至少有二棵二叉树 
  {
  p1=f->link;
  p2=p1->link;
  f->link=p2->link;           //取出前两棵树 
  t1=p1->root;
  t2=p2->root;
  free(p1);                 //释放p1 
  free(p2);                 //释放p2 
  t=(ptree *)malloc(sizeof(ptree));//开辟新的结点空间 
  t->w = (t1->w)+(t2->w);         //权相加 
  t->lchild=t1;
  t->rchild=t2;             //产生新二叉树 
  f=inforest(f,t);          //每次构造一颗二叉树的时候，都要从新排列一下 
  }//while 
  p1=f->link;
  t=p1->root;
  free(f);
 return(t);                  //返回t 
 }
 
pforest *inforest(struct pforest *f,struct ptree *t)
{
//按权值从小到大的顺序将结点从上到下地挂在一颗树上       
struct pforest *p, *q, *r;
struct ptree *ti;
r=(pforest *)malloc(sizeof(pforest)); //开辟新的结点空间 
r->root=t;
q=f;
p=f->link;              
while (p!=NULL)            //寻找插入位置 
 {
   ti=p->root;
   if(t->w > ti->w)          //如果t的权值大于ti的权值 
     {
         q=p;
      p=p->link;             //p向后寻找 
     }//if 
   else 
      p=NULL;                  //强迫退出循环 
  }//while 
r->link=q->link;
q->link=r;                 //r接在q的后面 
return(f);                 //返回f 
}
 
void InPut(int &n,int w[m])
{
printf("please input the sum of node/n"); //提示输入结点数 
scanf("%d",&n);      //输入结点数 
printf ("please input weight of every node/n"); //提示输入每个结点的权值 
for(int i=1;i<=n;i++)
scanf("%d",&w[i]);  //输入每个结点权值 
}
 
int main( )
{
struct ptree *head;
int n,w[m];
InPut(n,w);
head=hafm(n,w); 
travel(head,0);
printf("The length of the best path is WPL=%d", WPL);//输出最佳路径权值之和 
return 1;
}

posted @ 2013-06-05 16:34 Neo. 阅读(483) 评论(0) 编辑收藏举报

刷新页面返回顶部

热爱生命

数据结构（三）树、二叉树、最优二叉树

数据结构（三）树、二叉树、最优二叉树

公告