Attention Points

Attention Points

数组范围

  1. 无向图、树，边表的范围是边数的两倍。
  2. 因为最近树的题目做的比较多，一定要注意分清是树还是图，不能冲上去就去开struct Edge{int to,ne,w;}g[N<<1];
  3. 在做与走一个二维格子相关的问题时候，用组合数求方案，一定要注意阶乘和逆元相关的数组要开二倍
  4. 有些图论的题目需要加一些辅助点的题，一定要注意点集、边集的大小都要随之扩大
  5. 网络流因为需要建反向边，所以自带二倍的边表空间！！！！如果还要继续建边，那要继续往上乘！！！
  6. \(Manacher\)字符串一定要开二倍空间，后缀自动机同理。这些都是自带的。如果不放心，最好直接把\(N\)就开上二倍。如果需要在后面继续做DP啥的，也要开好！！！
  7. 用欧拉序的LCA，注意存欧拉序列的数组，以及RMQ的数组，还有算\(\log\)的数组，都要开二倍！！
  8. Kruskal重构树，点集是原点集的二倍！然后这下子基本上所有数组都是二倍了，可以直接把\(N\)设成\(2\)倍的。
  9. 主席树的题目，数组范围主要看Insert函数调用次数来分析。

边界控制

  1. 树链剖分的题目，如果是要把边权转化为点权，那么如果跳到最后跳到了\(x,\ y\)两个点重合，这个时候就不能再跑线段树的修改。这种错误在模板题里面基本上如果写的不是太烂基本上不会显现出危害来，因为线段树会自动在叶子停掉。但是在一些特别的题目中，要注意一定要判断。例题：牛客网NOIP赛前集训营-提高组（第六场） C 树
  2. 树状数组虽然写起来方便但是需要注意很多边界条件。比如说，\(lowbit\)这种东西，对\(0\)无效。所以，遇到树状数组需要存\(0\)这个数的，要把\(0\)单独特判一下。其实也很方便，每次修改时\(s[0]\)单独改一下，取用时\(s[0]\)直接赋为初值。
  3. 二分答案：如果里面的转移是\(l=mid\)，一定要注意是\(mid=(l+r+1)>>1\)。另外，还要仔细思考一下到底应该写\(l=mid\)还是\(l=mid+1\)。（其实有一种通用版的二分格式，但是那个比较暴力我不太喜欢）
  4. 二分答案的无解应该用什么标志判断？是\(l,r\)的值不正常，还是要用特殊的标记记录一下？
  5. 像DP或者递推这样的东西的初始状态一定要设置好。还有DP的时候加加减减，经常容易超过题目要的范围。
  6. DP的时候，一定要注意状转方程里面的转移，有没有超过定义范围，如果超过了，那么应该是视为不存在还是用特殊值补上还是这个算法就废掉了。
  7. 做最短路或者DP之类的东西，取最小值的话初值最好设置成\(0x3f3f3f3f\)也就是memset(dp,0x3f,sizeof(dp))。如果是要取最大值，如果不涉及到太多，无效状态不会干扰转移，可直接用\(0\)，否则memset(dp,0xc0,sizeof(dp))。上述两种值分别对应\(1061109567\)和\(-1061109568\)。
  8. 对于需要取模的题目，一般都是要模\(998244353\)或者\(10^9+7\)的，这样的话，加减不要取模，直接减。乘除一定要记得强制类型转换(ll)。

输入输出格式

  1. 尽量输出末尾换行，每一行后面不留空格，以防评测方式为逐字节比较。
  2. 同一行输出的数之间是用什么隔开的，空格？限制场宽？（不过好像基本没遇到过，只有普及组的无聊练习题才会有。
  3. 输入的数之间有没有空格？数据是用什么分隔？（空格？逗号？逗号基本没有遇到过，也是基本上只有普及组的无聊题才会用）
  4. 文件是用什么结尾的？\(n=0\)?EOF?专门的字符串？
  5. 无解输出的是什么？\(-1\)？\(0\)？No solution？No answer？……
  6. 仔细阅读输入格式，有没有多组数据？（好像基本上只有\(POJ\)和\(HDU\)喜欢这样）对应的输出要不要用空行分隔？要不要用输出Case #1: 32什么的？
  7. 计算几何的题目，一定要看清出输入时浮点数还是整数，不要以为样例是整数就当整数来输入。

特殊错误

  1. 输出中间变量的调试信息有没有删掉或者注释掉？

  2. 写的一些很重要的函数真的调用了吗？比如线性筛啊，线段树的Build呀，欧拉序LCA的RMQ_init……

  3. 调用函数的时候打上了函数名了没?如果不打，编译器会把它当成一个括号里面是逗号表达式，不仅可以通过编译，而且可能还会通过一些比较弱的样例。

    解决技巧：编译选项中加上-Wall

  4. 时刻注意，C++的运算符优先级问题

img

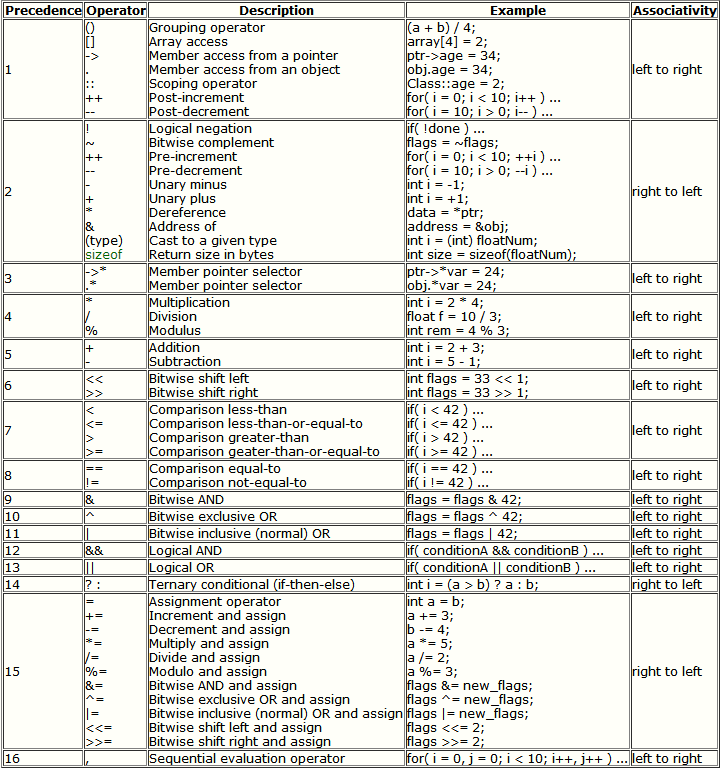
  1. 有时候，为了方便，会写return write(ans),0;一定不能把,0给忘掉，不然main函数返回值非0就要RE了。
  2. 提交程序的时候不要忘记加上文件。
  3. 自己用来调试输出中间变量的调试信息有没有删掉？（貌似经常犯这种错误）
  4. 有没有把==符号打成=？再或者，发过来，有没有把=打成==？这两种错误基本上还是很容易犯的，而且一般样例都测不出来，编译器还不会报错。（因为C++的自动类型转换功能太强了，会自动把int转为bool操作。而且单独一个没有意义的值，编译器也会认为是一个语句来操作）
  5. 注意memset不能老用。每一次memset是要遍历完整个数组的。对于只是保证运算的总次数不超过一定值的题目，不能都memset（比如点分治，还有zby学长今天利用题面的一个保证的细节叉掉的20181108模拟T2 循环依赖）。
  6. 还有一种情况也尽量不要用memset：每一次操作只会用到一个数组里面的几个值，用的值的数量远小于数组大小，这样的话最后就是直接记下用过哪些位置，用for循环来初始化。

关键字&C++语法问题

  1. 经典关键字：y1,next,search,find,pipe（这个是系统关键字）,friend,out,end,link,pre
  2. 比较好的解决方法：不要写using namespace std;。用的时候直接std::max(a,b)或者using st::max;
  3. 更好的解决方法：对于有实际意义作为函数名或者变量名的，首字母大写（函数名首字母大写很好看，但是变量名首字母大写真的不好看）
  4. pair是utility库里面的模板，但是只需要包含algorithm大概就够了。

阅读题目问题

  1. 题目里面的坐标是指OI中常见的那种坐标的方向，还是数学里面坐标的方向？
  2. 注意题目给你的是排列还是排名？
  3. 题目有一些关键性的提示：“保证每个点的度均不超过20”或者“保证数据随机”什么的。
  4. 注意分析题目的要点，比如一些假的限制条件。不怎么好说，「20181102模拟」华莱士 应该就有一个假的限制条件来骗人的。
  5. 有些题目的核心数组不是用\(n\)来表示的，对于这些题目，一定要好好注意，不能顺手就写成了\(n\)这样的话，容易出很多样例测不出来的错误。
  6. 对于概率期望的题目，不要冲上去就直接用概率期望进行计算或者DP。有些概率期望题目可以转化为计数或者求和的题目。

思路

  1. 尽可能从题目中概括出题意。对于一些题目，可以把一些操作适当的分裂，转化为几个好思考的小操作。
  2. 最好把复杂的题意简化，这样利于思维。
  3. 不要把思维局限在一种想法上，如果一个思路实在思考不出来，可以忘掉刚才想的，换条路子走。
  4. 不要受题目顺序拘泥，先通览题目，做简单思考与难度预估。
  5. 如果在一道题上面用的时间太多，那么最好先暂时放下这道题，先去思考思考别的题目。
  6. 想算法一定要及时分析复杂度，很有可能想到了一个实际复杂度比表面上低的算法，或者漏考虑了什么东西导致复杂度想低了。
  7. 一定要把想的算法从头到尾理通了在写，万一有什么细节没想到，那么时间浪费得就不值得了。
  8. 有的时候，对于实在想不出正解的题目，如果发现答案在所有情况中，是很多情况的一个子部分，可以考虑随机化。（不能瞎随机，一定要有概率保证，不然随机基本无望算法答案）

特殊思路

下面罗列集中套路一样的思路：

  1. 树上的和最远有关的题目——树的直径

  2. 塞方块的题目——递推

  3. 分析以后转化成奇偶环——二分图染色

  4. 可以得到几组条件要求一些点相互对立——二分图染色

  5. 方格图上的方案数、最优值——DP或者组合计数

  6. 确定一个最优值、且在最优值以内一定可行——二分答案

  7. 与时间相关并且不同事件可以同时发生的最优化问题——二分答案

  8. 每一次只修改一个位置——主席树

  9. 字符串的比较问题——哈希

  10. 从几个值慢慢推到一个值——写式子找规律

  11. 和一个数字中每一位有关——数位DP

  12. 有确定的初状态和末状态——最短路或者BFS或者DP

  13. 一段区间内的答案可以直接求，最后是很多很多区间价和起来——序列DP 例：「20181026模拟」狐狸的谜语

  14. 对于和集合有关的题目，并且集合大小比较大，不能状压DP的题目，可以考虑写式子，然后化式子。

    例：「20181101模拟」dice 「20181108模拟」任务分配（其实这道题不用推式子也可以得出结论）

  15. 对于每一个区间的答案具有价和性的题目，可以考虑用线段树维护（包括哈希值也可以用线段树维护）。

    如果线段树不太方便维护，可以把询问离线，然后分治询问，每次统计过中点的询问。例：「20181031模拟」式神守护

  16. 对于统计一个区间里面一些数的存在性的问题，可以把询问离线用线段树来搞。例：「20181027模拟」mex

  17. 对于两个序列DP，如果一个序列比较大，另一个比较小，答案和小序列同阶的，一定要注意从小序列上设状态，并处理出小状态在大状态里面的一些信息。例：[NOIP2017模拟10-29]不可逆的重启动

  18. 对于式子非常奇怪的题目，并且参数的范围还比较大，可以试着分析其重要性质——收敛啊，规律啊…… 例：「20181031模拟」西行妖下

  19. 对于走路带有限制的最短路，可以试着把限制存下来跑。但是如果限制没法存，试分析、用更简短的限制概括一下。例：「20181030模拟」辉夜的夜空明珠

  20. 对于很多组不同排列统计信息的，试分开成每一个点、边、点对的贡献（很多种贡献统计方法都要考虑一下，不能钉在一种方法上）例：「20181030模拟」永琳的竹林迷径

  21. 图论中，对于以小规模（这里小规模是指时间能容许的）的信息为基础来计算出大规模信息来加边的题目，可以考虑建辅助点。例：「20181029模拟」山路

  22. 如果题目中有些操作，每次对序列的变动很大，可以尝试把大范围变化通过差分前缀和等手段简化为小变化，从而抓一下好计算，好维护的来思考。例：「20181027模拟」密码锁

  23. 也算是套路了：对于只有东西逐渐消失（也就是删除操作），考虑时间倒流，变成逐渐出现 例：「20181027模拟」打地鼠游戏 「20181020模拟」电线杆

  24. 对于很多状态有明显不优的，那么那些状态就可以直接废掉了，不需要再计算了，这是很重要的剪枝。例：「20181026模拟」最强大脑

  25. 直径的性质有很多，一定要好好熟悉。（很多树上的最长路都可以转化为直径）例：「20181106模拟」jcp 「20181024模拟」寻路

  26. 对于向下取整、整除、取余的题目，一定要尝试拆式子，把取整、整除、取余拆开来。

常用结论

  1. 线段树的本质不同的节点只有\(\log\)个，每一层的节点对应区间长度的大小相差不超过\(1\)
  2. 关于树的直径：
    1. 任意有两树合并起来的树，其直径的端点一定是原来两条直径的四个端点中的两个
    2. 一棵树的所有直径交于同一点，该点为直径的中点。从任何一个点到离它最远的点的路径，一定经过这个中点，且到达某一个直径的端点。
    3. 距某个点最远的叶子节点一定是树的某一条直径的端点
  3. 在一个连通无向无环图中，\(x\)、\(y\) 和 \(z\) 是三个不同的结点。当 \(x\) 到 \(y\) 的最短路与 \(y\) 到 \(z\) 的最短路不重合时，\(x\) 到 \(z\) 的最短路就是这两条最短路的拼接。

技巧

  1. 对于数据生成器以及暴力都比较好写的题目一定要顺手对拍一下。
  2. 快读千万不能打错。对于数据范围比较小的，最好不要用快读。快读尤其注意有没有写折构函数来flush，以及读入、输出对于负数和\(0\)的处理。
  3. 分析题目的时候一定要手画一下机组样例以及自己的数据，说不定能发现什么或者启发什么思路。
  4. 需要计算组合数，但是却没有取模操作，如果可保证答案在一定范围以内，可以用在范围外的一个数来进行假取模。

特殊算法/数据结构总结

  1. 线段树的区间修改有没有写成假的（比如写成了暴力)。修改和下传有没有及时pushdown和pushup。
  2. 线段树的叶子节点不要pushup！！！！！
  3. 树链剖分的while(top[x]!=top[y])不要写成if(top[x]!=top[y])。
  4. 并查集一定要初始化！！！（不过这种错误一般样例就能测出来了，但是把不必要的时间丢在这上面是在是浪费）
  5. 二分答案，最后一步二分的，不一定是最终答案。所以对于二分的内容并不直接就是答案的题目，二分完以后，还要再计算一遍答案，不能直接用最后一次的结果！！！
  6. DP用了滚动数组的题目，因为当前数组可能还会记录着上一次的值，要注意清空。（但是又不清空仍然是对的的题目：20181108的模拟T3，写了一个滚动数组忘了每次都初始化，结果竟然A掉了，后来分析了一下正确性，对于这道题不初始化确实是对的，但是对别的题目不一定是对的）
  7. 对于图论的题目，一定要注意分析像重边、自环对自己算法正确性的影响。
posted @ 2017-10-18 23:46  hankeke303  阅读(434)  评论(0)  编辑  收藏  举报