XMU《计算方法》实验一 三次样条插值算法
实验一 三次样条插值算法
一、Matlab 代码
clear; x = input('请输入插值结点的 x:'); y = input('请输入插值结点的 y:'); [x, I] = sort(x); y = y(I); if length(y) ~= length(x) error('x 和 y 的数量不相等!'); end n = length(x) - 1; N = n * 4; % 函数值约束 A = []; b = []; for i = 1:n a = zeros(1, N); a(4*i-3 : 4*i) = [x(i)^3, x(i)^2, x(i), 1]; A= [A; a]; b = [b; y(i)]; a(4*i-3 : 4*i) = [x(i+1)^3, x(i+1)^2, x(i+1), 1]; A = [A; a]; b = [b; y(i+1)]; end % 一阶导数连续约束 for i = 2:n a = zeros(1, N); a(4*i-7 : 4*i) = [3*x(i)^2, 2*x(i), 1, 0, -3*x(i)^2, -2*x(i), -1, 0]; A = [A; a]; b = [b; 0]; end % 二阶导数连续约束 for i = 2:n a = zeros(1, N); a(4*i-7 : 4*i) = [6*x(i), 2, 0, 0, -6*x(i), -2, 0, 0]; A = [A; a]; b = [b; 0]; end type = input('请输入边界条件类型(0: 自然边界条件;1: 一阶导;2: 二阶导):'); if type == 0 % 自然边界条件约束 a = zeros(1, N); a(1:4) = [6*x(1), 2, 0, 0]; A = [A; a]; b = [b; 0]; a = zeros(1, N); a(4*n-3 : 4*n) = [6*x(n+1), 2, 0, 0]; A = [A; a]; b = [b; 0]; elseif type == 1 y0 = input(strcat('请输入 x=', num2str(x(1)), ' 处的一阶导:')); yn = input(strcat('请输入 x=', num2str(x(n+1)), ' 处的一阶导:')); a = zeros(1, N); a(1:4) = [3*x(1)^2, 2*x(1), 1, 0]; A = [A; a]; b = [b; y0]; a = zeros(1, N); a(4*n-3 : 4*n) = [3*x(n+1)^2, 2*x(n+1), 1, 0]; A = [A; a]; b = [b; yn]; else y0 = input(strcat('请输入 x=', num2str(x(1)), ' 处的二阶导:')); yn = input(strcat('请输入 x=', num2str(x(n+1)), ' 处的二阶导:')); a = zeros(1, N); a(1:4) = [6*x(1), 2, 0, 0]; A = [A; a]; b = [b; y0]; a = zeros(1, N); a(4*n-3 : 4*n) = [6*x(n+1), 2, 0, 0]; A = [A; a]; b = [b; yn]; end % 解方程并将解对应还原到各个样条三次插值的系数 p = A \ b; a = []; b = []; c = []; d = []; for i = 1:n a(i) = p(4 * i - 3); b(i) = p(4 * i - 2); c(i) = p(4 * i - 1); d(i) = p(4 * i); fprintf('f(x) = %gx^3 + %gx^2 + %gx + %g\tx in [%g, %g]\n', a(i), b(i), c(i), d(i), x(i), x(i+1)) end % 计算各个给定点的插值结果 X = linspace(x(1), x(n+1), 200); Y = []; m = length(X); for i = 1:m for j = 1:n if X(i) >= x(j) && X(i) <= x(j+1) Y(i) = a(j)*X(i)^3 + b(j)*X(i)^2 + c(j)*X(i) + d(j); end end end % 画图 hold on; plot(X, Y); plot(x, y, 'o');
二、算法原理
三次样条插值应该满足以下条件:每一小段都是三次多项式,且整体的二阶导数连续。
思路:
给定插值节点 \((x_0, y_0), (x_1, y_1), \dots, (x_n, y_n)\)。
三次样条插值函数:
一共需要确定 \(4n\) 个未知数。
限制 1——函数值约束
提供了 \(2n\) 个限制。
限制 2——一阶导数连续约束
提供了 \(n-1\) 个限制。
限制 3——二阶导数连续
限制 4 ——边界条件
在本程序中,我们实现了三种边界条件,分别是边界一阶导约束、边界二阶导约束和自然边界条件。
(1)自然边界条件
化作多项式的形式,即
(2)一阶导约束
化作多项式的形式,即
(3)二阶导约束
化作多项式的形式,即
限制的矩阵形式
因为不同的边界条件对应不同的矩阵最后两行,这里以自然边界条件的矩阵为例。
设 \(\boldsymbol x = [a_1, b_1, c_1, d_1, \cdots, a_n, b_n, c_n, d_n]^T\)。
则上述方程组可以写成 \(\boldsymbol{Ax}=\boldsymbol b\) 的形式,即
三、程序说明
在“二”的最后,我们得到了一个 \(\boldsymbol{Ax}=\boldsymbol b\) 形式的矩阵。我们只需要在 Matlab 中表示出这个矩阵,通过 Matlab 的 A \ b 运算,即可得到 \(\boldsymbol x\) 的解。
在计算出 \(x\) 之后,我们根据我们设计 \(\boldsymbol x\) 的原理,每相邻的四项属于同一个三次多项式,即可得到我们的三次样条插值函数了。
如果需要计算一个 \(x\) 的插值结果,我们只需要判断 \(x\) 属于样条插值的哪一段,然后使用这一段的三次多项式函数计算,即可得到 \(x\) 的解。
在程序中,我们通过画出图像的方式,直观地表现了三次样条插值的结果。其中,插值节点我们使用圆形点出,插值函数我们使用一条连续实线绘制而成。
值得注意的是,为了提高程序的通用性,我们考虑了输入的插值节点并没有按照 \(x\) 坐标排序的情况,因此我们在程序中重新对所有点的节点按照 \(x\) 坐标进行了排序。
此外,我们考虑到了边界条件的多样性,因此提供了三种不同的边界条件约束,在程序中,我们对用户需要的边界条件约束类型进行提问,一次设计不同的系数矩阵,来计算插值的结果。
程序中,除了解线性方程组和使用 plot 绘制图像的过程,全部独立完成,包括线性方程组的建立,矩阵的描述和表示,以及计算插值,计算绘制图像需要的点坐标的过程,全部是我们自己实现的,没有调用任何的 Matlab 工具。
四、运行结果示例
示例 1

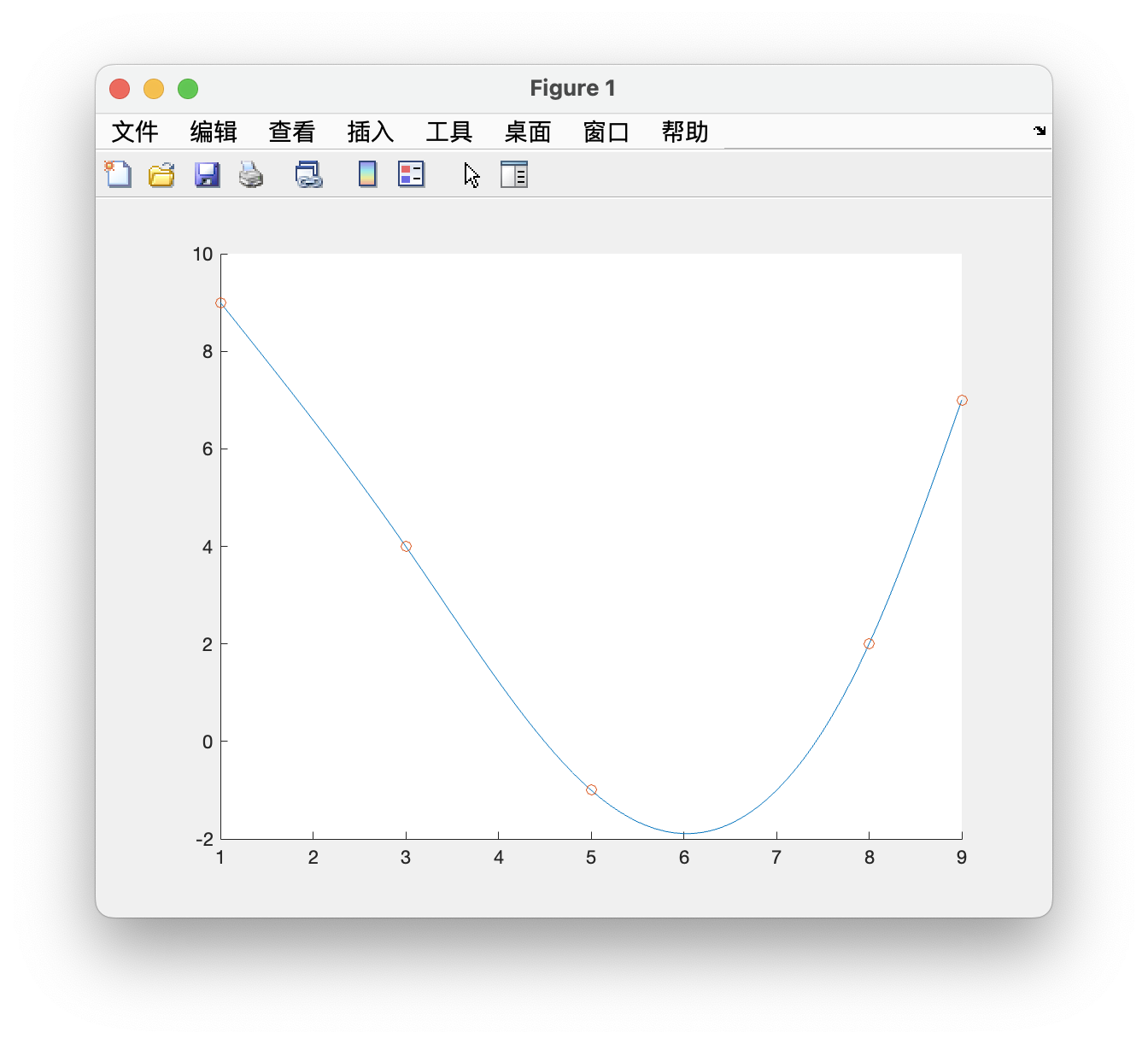
示例 2

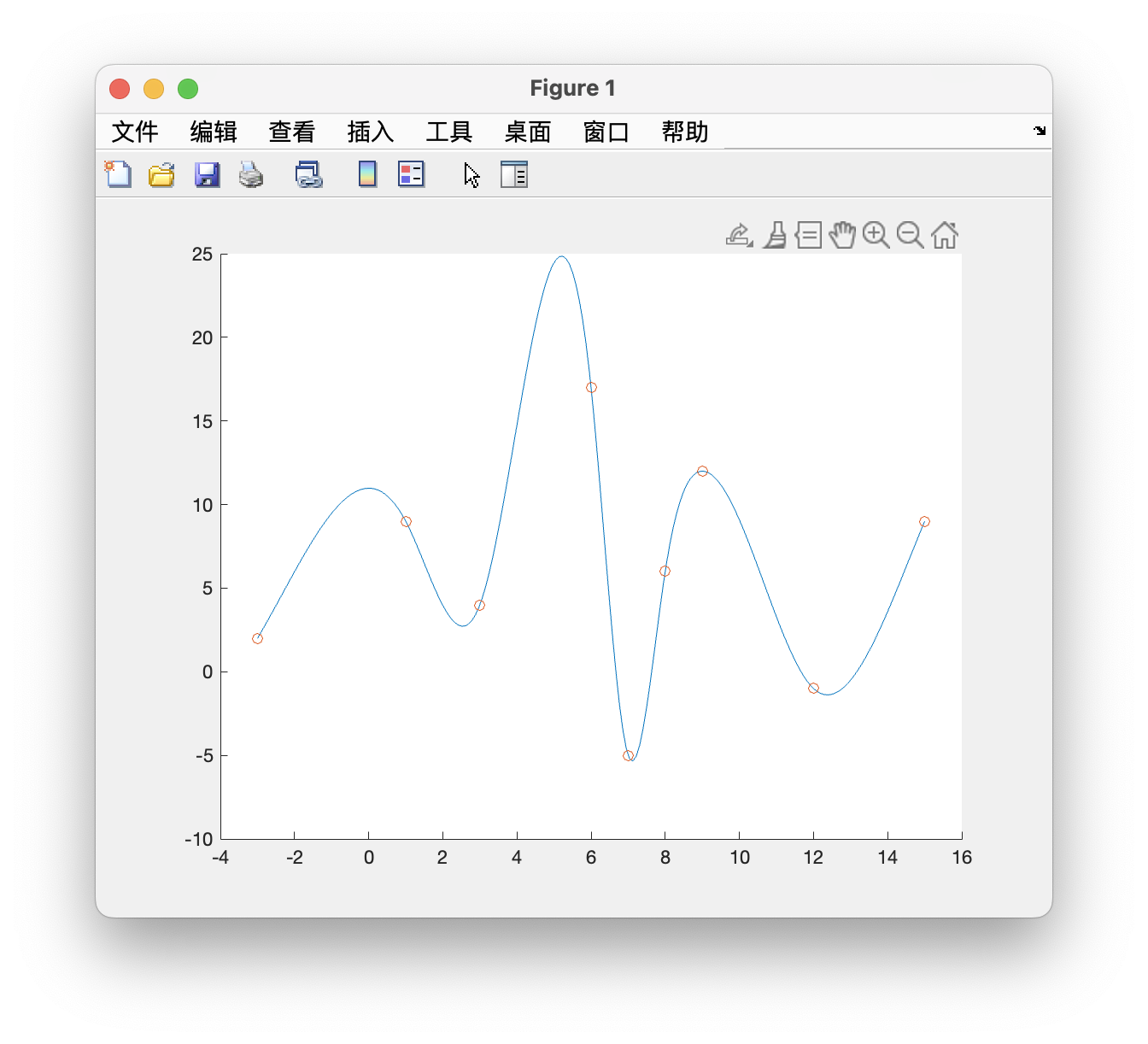
示例 3

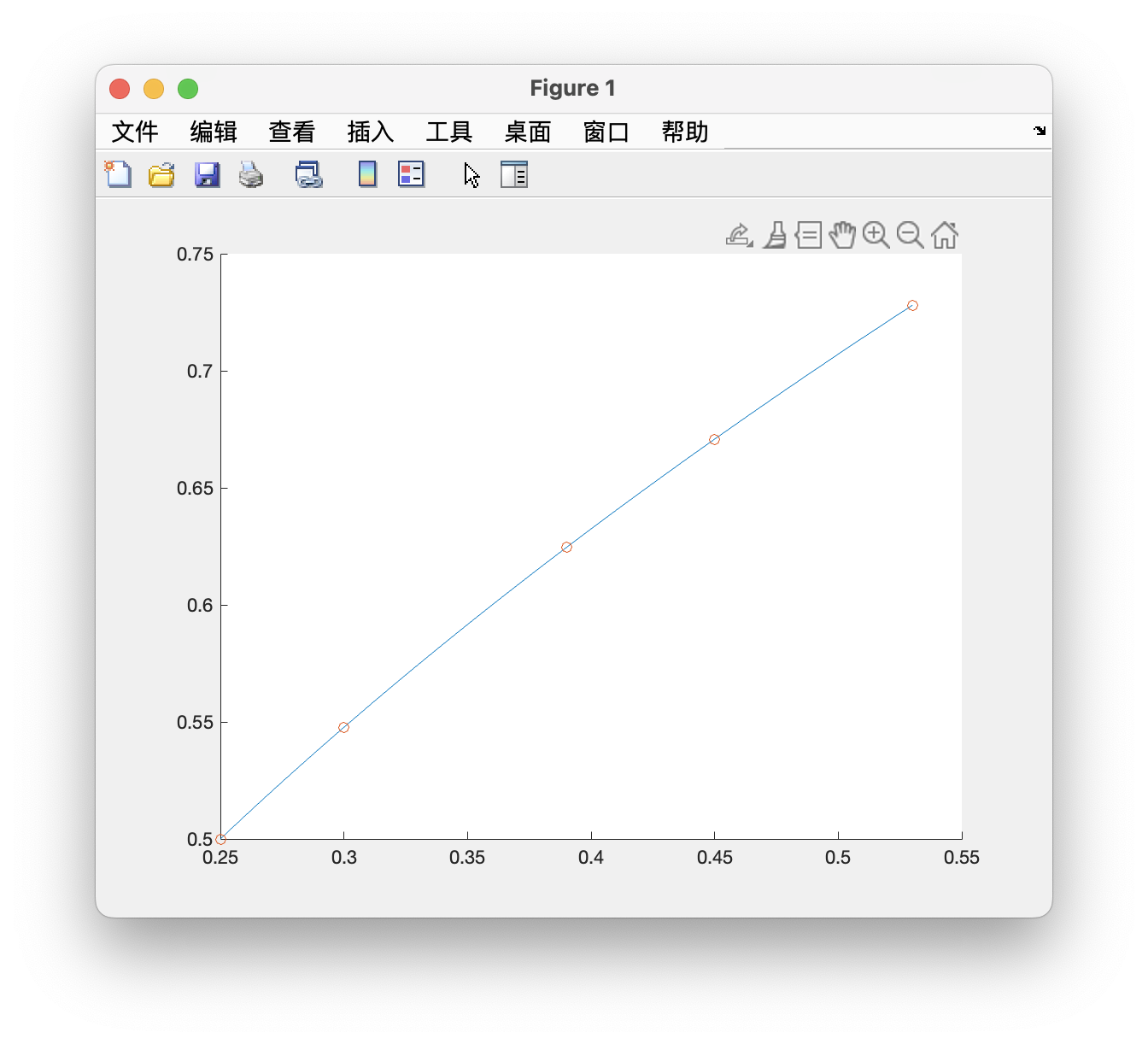



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!