CSAPP Lab-5 Cache Lab

到实验 5 啦！

这次的实验是有关高速缓存的。

让我们先来复习一下高速缓存的基础知识吧！

复习

高速缓存的结构

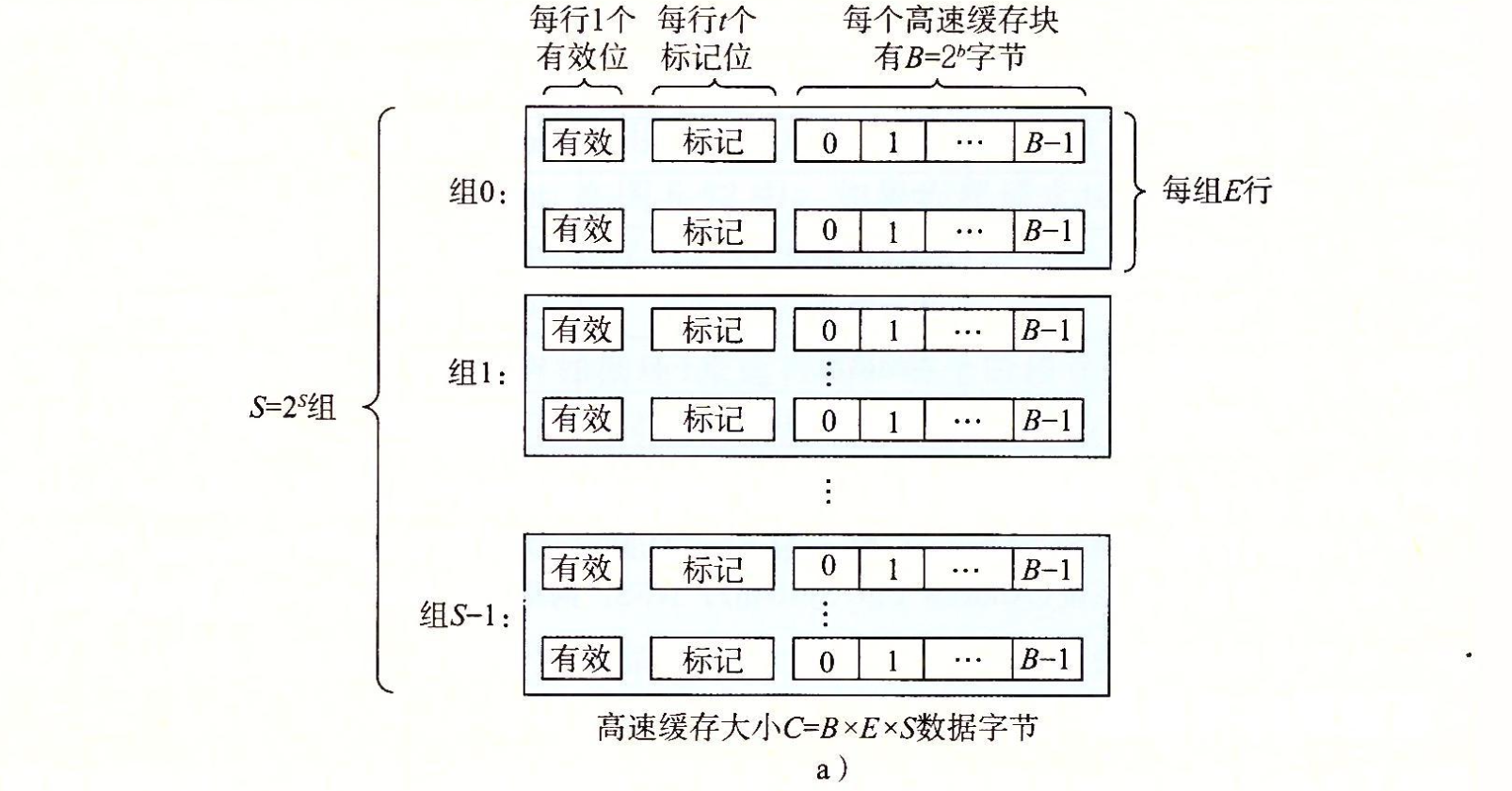
在一个存储器地址有 \(m\) 位的系统上，一共有 \(M = 2^m\) 个地址。假设高速缓存被组织成一个有 \(S = 2^s\) 个高速缓存组的数组，其中每个组包括 \(E\) 个高速缓存行，每行存储一个大小为 \(B = 2^b\) 的数据块。每行中还有一个有效位指明该行中是否有存放有效数据，\(t\) 个标记位可以用来来配合组号唯一确定存放在这个行中的块。

\(C = S\times E \times B\) 就是高速缓存的大小。

地址的结构

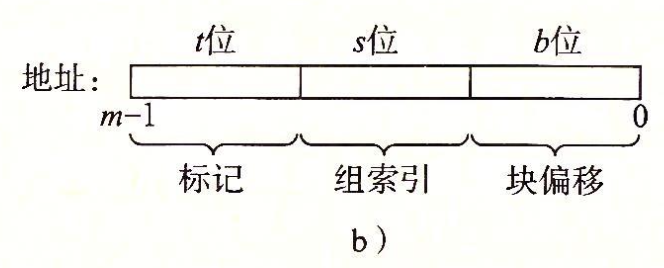
那么，如何确定一个地址应该放在什么位置呢？

高速缓存的参数 \(S\) 和 \(B\) 将每个地址分成了三段。每个地址最低的 \(b\) 位是块偏移，高速缓存中每个块都是连续的 \(B\) 个地址上的数据，块偏移就是用来确定这个地址会位于所在块的那个位置。

第 \(b\) 到 \(b + s - 1\) 位是组索引，用来确定这个地址应该存在高速缓存块中哪一个组里。

而当把一个数据块放进高速缓存中时，剩下的最高 \(t\) 位就是存在高速缓存行中的标记位。也就是说，一定会有 \(t + s + b = m\)。

高速缓存的替换策略

有了前面的基本知识，高速缓存的组选择是很容易理解的。如果我们确定了需要访问的地址的组编号，可以很快定位到这个组中。

如果这个组中有我们需要的块，那么可以直接返回命中结果。

如果组中没有我们需要的块，那么如果组中仍有空位，那么可以从内存中取出这个块存放在组里。但是，如果缓存组已经满了，那么就需要选择一行替换掉。那么该选择哪一行呢？

书上提供了两种常用的策略：

• 最不常使用（LFU）：替换在过去某个窗口时间内引用次数最少的那一行。
• 最近最少使用（LRU）：替换最后一次访问时间最久远的那一行。

实验中让我们使用的策略是 LRU。

Part A: Writing a Cache Simulator

A 的任务很简单，只需在 csim.c 中模拟高速缓存的实现，可以根据提供的内存访问记录的文件来给出命中、不命中和驱逐的统计。这个程序还需要实现对于命令行参数的加载。

所谓的内存访问记录，是使用命令 valgrind 来得到的，其输出是这样的结构：

[space]operation address,size

其中，operation 是 I, M, L, S 中的一种，I 代表指令加载，L 代表数据加载，S 代表数据存储，M 代表数据修改。而 address 是操作的内存地址，size 是操作的数据大小。

分析

因为实验要求中，我们不需要关心指令加载的操作。同时，实验也假设了内存访问被对齐得很好，不会出现一次访问的范围超出了一个块的情况，因此也不需要关心 size。

而 L, S 操作都是对内存的简单访问，M 就相当于是先 L 再 S，而在本实验中，L 和 S 是不做区别的，因此不管是什么操作，都可以看做一次或两次简单的数据访问，在我们的程序中，使用 access(addr) 函数来解决就可以了。

数据表示

typedef struct {            // 结构体：高速缓存行
    bool valid;             // 有效位
    unsigned tag;           // 标记位
    unsigned lastVis;       // 上一次访问的时间
} CacheLine;
typedef struct {            // 结构体：高速缓存组
    CacheLine *lines;       // 组中的所有行
    unsigned count;         // 组中存放有效数据的行数
} CacheSet;
typedef struct {            // 结构体：高速缓存
    CacheSet *sets;         // 高速缓存的所有组
    unsigned S, s;          // 组数
    unsigned E;             // 行数
    unsigned B, b;          // 块大小
    unsigned time;          // 高速缓存的“时间”
} Cache;

我们使用三个结构体分别表示一个高速缓存行、一个高速缓存组和一个高速缓存。

高速缓存的时间表示

你很有可能已经注意到了，在 Cahce 结构体中已经存在了一个 times 成员变量。这就是我们的高速缓存时间。

高速缓存时间是为了标识每个高速缓存行最后一次访问的时间先后，以此来确定要驱逐的行。但是高速缓存时间是怎么设定的呢？

我们注意到，只有在访问数据的时候，会引起每个行的「最后访问时间」发生变化，其余的时间对于替换策略没有什么意义。因此，我们可以在每次访问数据的时候，将高速缓存的 time 加一，以此来决定高速缓存的时间。

Cache ca;
void initCache(int s, int E, int b) {
    ca.s = s, ca.E = E, ca.b = b;
    ca.S = 1 << s, ca.B = 1 << b;
    ca.sets = (CacheSet *)malloc(sizeof(CacheSet) * ca.S);
    for (unsigned i = 0; i < ca.S; ++i) {
        ca.sets[i].count = 0;
        ca.sets[i].lines = (CacheLine *)malloc(sizeof(CacheLine) * E);
        for (unsigned j = 0; j < E; ++j)
            ca.sets[i].lines[j].valid = 0;
    }
}

void access(unsigned addr) {
    ++ca.time;
    // ...
}

一些封装了的操作

在一个组中根据 tag 查找行

简单地扫描组中的所有行即可，因为查找只会发生在数据访问中，所以可以顺便设置一下时间。

CacheLine *findLine(CacheSet s, unsigned tag) {
    for (unsigned i = 0; i < s.count; ++i)
        if (s.lines[i].valid && s.lines[i].tag == tag) {
            s.lines[i].lastVis = ca.time;
            return &s.lines[i];
        }
    return NULL;
}

加载一个新的行

这里写了两个函数，第一个负责在一行设置有效位、标记位和时间，另一个负责在一组中新开一个行（在组没有满的时候）。

void setLine(CacheLine *l, unsigned tag) {
    l->valid = 1;
    l->tag = tag;
    l->lastVis = ca.time;
}
void newBlock(CacheSet *s, unsigned tag) {
    setLine(&s->lines[s->count], tag);
    ++s->count;
}

执行 LRU 策略

就是在一组已满的时候，执行 LRU 策略，找出最后访问时间最早的行。直接模拟即可。

CacheLine *findLRU(CacheSet s) {
    unsigned id = 0;
    for (unsigned i = 1; i < ca.E; ++i)
        if (s.lines[i].lastVis < s.lines[id].lastVis)
            id = i;
    return &s.lines[id];
}

访问数据

大致思路就是先锁定组号，计算标记位。根据我们前面复习的，一个地址前 \(t\) 位是标记位，中间的 s 位是组号，最后的 b 位是偏移，因此标记位可以通过 addr >> (b + s) 计算，组号需要先右移 b 位以后对低 s 位取 and。

然后取出这个组，在组中查找标记是否存在。如果不命中，再判断组是否已满。如果已满就驱逐一行，否则直接接着放置即可。

在每一种情况确认以后，记得修改命中、不命中、驱逐计数器，以及在 verbose 模式下需要输出。

int hitc, missc, evic;
void access(unsigned addr) {
    ++ca.time;
    unsigned tag = addr >> (ca.b + ca.s), set = (addr >> ca.b) & (ca.S - 1);
    CacheLine *l = findLine(ca.sets[set], tag);
    if (l) {
        if (verbose) printf(" hit");
        ++hitc;
        return;
    }
    if (verbose) printf(" miss");
    ++missc;
    CacheSet *s = &ca.sets[set];
    if (s->count == ca.E) {
        if (verbose) printf(" eviction");
        ++evic;
        CacheLine *ev = findLRU(*s);
        setLine(ev, tag);

    } else newBlock(s, tag);
}

读取 trace 文件

如前面所述，L 和 S 操作都可以看做一次 access，M 操作可以看作两次 access。根据情况调用 access 函数即可。

注意 verbose 模式下需要输出记录。

void readTrace(FILE *fp) {
    char opt;
    unsigned addr, size;
    while (fscanf(fp, " %c %x,%u", &opt, &addr, &size) > 0) {
        if (opt == 'I') continue;
        if (verbose) printf(" %c %x,%u", opt, addr, size);
        if (opt == 'M') access(addr), access(addr);
        else if (opt == 'L') access(addr);
        else if (opt == 'S') access(addr);
        if (verbose) printf("\n");
    }
    fclose(fp);
}

读取命令行参数

实验文档中建议我们使用 getopt 函数。

简单介绍一下，这个函数可以从命令行参数中一个个筛出有效的参数或者无效的信息：

int getopt(int argc,char * const argv[ ],const char * optstring);

这个函数的前两个参数和 main 函数的参数格式是相同的，分别是命令行参数的数量和命令行参数构成的字符串数组。第三个参数是命令选项，形如 ab:c:de，其中每一个字母 x 代表着接受一个 -x 的选项，字母后面接着 : 代表这个 -x 参数后面必须带有一个选项参数。

这个函数会依次扫描每一个命令行参数，如果不匹配我们提供的选项会输出报错，如果匹配了会返回匹配到的选项名（字符形式），同时在 optarg 这个全局字符指针中存储这个选项对应的参数。如果扫描结束，返回值会是 \(-1\)。

我们简单利用一下这个函数就可以成功读取命令啦！

bool verbose;
void printHelp(char *file);

int main(int argc, char **argv) {
    int s = -1, E = -1, b = -1;
    char opt;
    FILE *fp = NULL;
    while ((opt = getopt(argc, argv, "hvs:E:b:t:")) != -1) {
        switch (opt) {
            case 'h':
                printHelp(argv[0]);
                return 0;
            case 'v':
                verbose = 1;
                break;
            case 's':
                s = atoi(optarg);
                break;
            case 'E':
                E = atoi(optarg);
                break;
            case 'b':
                b = atoi(optarg);
                break;
            case 't':
                fp = fopen(optarg, "r");
                if (fp == NULL) {
                    printf("%s: No such file or directory\n", optarg);
                    return 0;
                }
                break;
            default:
                printHelp(argv[0]);
                return 0;
        }
    }
    if (!~s || !~E || !~b || !fp) {
        printf("Missing required command line argument\n");
        printHelp(argv[0]);
        return 0;
    }
    initCache(s, E, b);
    readTrace(fp);
    printSummary(hitc, missc, evic);
    return 0;
}

完整程序

完整程序太长啦，大家可以点击 这个链接 来下载！

贴一下得分：

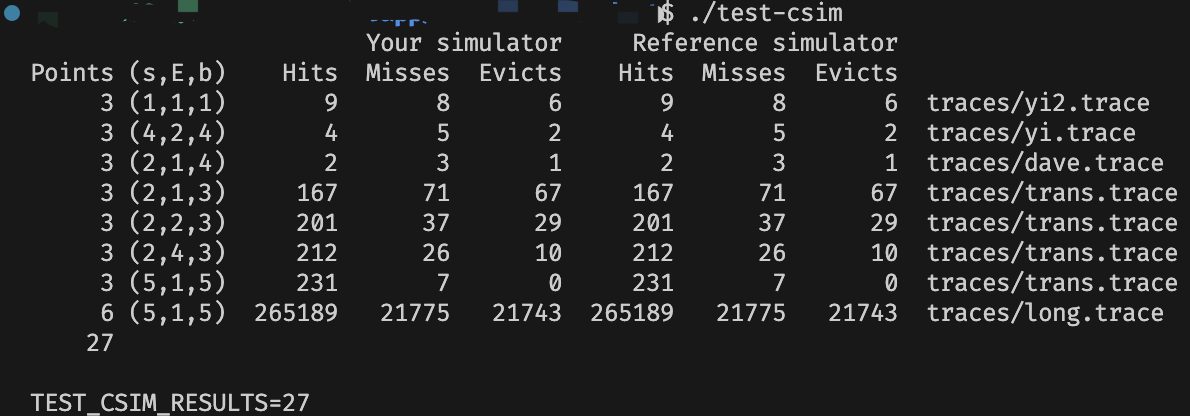
Part B: Optimizing Matrix Transpose

终于到 Part B 啦。Part B 的主要任务是优化一个矩阵转置的程序，使得它在一个 \(s = 5, E = 1, b = 5\) 的高速缓存上，不命中的次数最少。

这个部分实验主要想让我们学习一种叫作「分块」的技巧。具体的知识可以参考文档中提供的资料：http://csapp.cs.cmu.edu/public/waside/waside-blocking.pdf 。

这里贴一张书上给出的简单介绍以供参考。

默认的矩阵转置代码，不做优化的是这个样子的：

void trans(int M, int N, int A[N][M], int B[M][N])
{
    int i, j, tmp;

    for (i = 0; i < N; i++) {
        for (j = 0; j < M; j++) {
            tmp = A[i][j];
            B[j][i] = tmp;
        }
    }    

}

一共分为 \(3\) 个子任务，每个子任务都需要达到一定的优化目标，具体的给分如下：

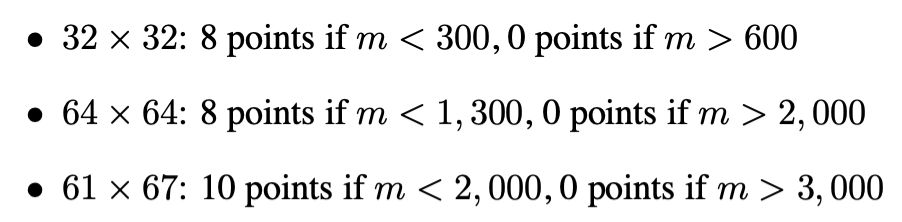
\(32 \times 32\)

首先看一下如果不做优化的不命中次数是多少：

很显然，这个距离我们的目标还挺远的。先来理解一下这个 \(1183\) 是怎么计算出来的吧。

首先我们很容易发现，\(A\) 和 \(B\) 两个矩阵的首地址末 \(10\) 位都是相同的，也就是说，这两个矩阵的相同位置一定会出现在相同的高速缓存组中。

一个高速缓存块是连续的 \(2^5 = 32\) 字节，也就是 \(8\) 个 int 类型的变量，每行 \(8\) 个这样的块，所以整个高速缓存可以储存 \(\frac {32}4 = 8\) 行的矩阵。因此，如果按照外层枚举行内层枚举列的顺序，可以最高效率地使用缓存，一般可以达到每 \(8\) 个元素才会出现一次不命中，不命中总次数应该是 \(32 \times 32 \div 8 = 128\) 次。这就是 \(A\) 矩阵的估计不命中次数。

但是，如果按照 \(B\) 矩阵的枚举顺序，外层枚举列，内层枚举行，那么每次访问都会产生不命中（因为每个缓存块的内容，只会被使用一次，在下次使用之前这个块早就被驱逐了），因此 \(B\) 矩阵的不命中次数是 \(32 \times 32 = 1024\) 次。那么加起来，我们的预估总不命中次数应该是 \(1024 + 128 = 1152\) 次。比实际的要少 \(31\) 次，这是什么原因呢？

实际上，因为 \(A\) 和 \(B\) 矩阵是同时被访问的，因此 \(B\) 矩阵的操作会影响 \(A\) 矩阵的缓存。这种影响只会发生在转置对角线元素的时候，只有这个时候 \(A\) 和 \(B\) 会使用同一个缓存，对 \(B\) 的写会把 \(A\) 当前的缓存驱逐出去，因此下一次读 \(A\) 上同一个块的时候，会触发一次不命中。只有整个矩阵最后一个元素在写完以后不需要再读这个块，因此总共多了 \(31\) 次不命中。

知道了不命中的来源，怎么优化也就很明显了。可以观察到，主要的不命中都是 \(B\) 矩阵贡献的。如果我们能让 \(B\) 矩阵的缓存发挥左右，就可以解决这个问题。

每次在 \(B\) 矩阵上写 \(8\) 行就会触发一次驱逐，因此我们可以最多同时写 \(8\) 个块。所以思路很简单：

将 \(A\) 和 \(B\) 每个矩阵分成 \(4\times 4\) 个大小为 \(8\times 8\) 的块，每次将 \(A\) 上的一个块转置到 \(B\) 上对应的块中，一个块处理完再去处理下一个块。这样保证了 \(B\) 的缓存都被写完了才会驱逐。

代码很简单：

void transpose_32x32(int M, int N, int A[N][M], int B[M][N]) {
    for (int ii = 0; ii < 32; ii += 8)
        for (int jj = 0; jj < 32; jj += 8)
            for (int i = ii; i < ii + 8; ++i)
                for (int j = jj; j < jj + 8; ++j)
                    B[j][i] = A[i][j];
}

然而很遗憾，这个做法的不命中数依然比 \(300\) 多：

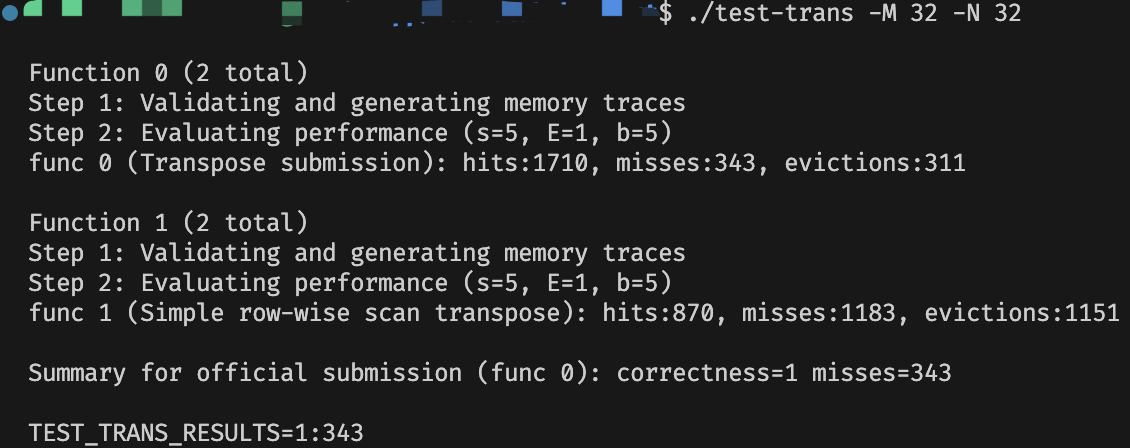
为什么会这样呢？注意到我们之前的朴素矩阵转置中，为什么不命中数会多了 \(31\)？那是因为对角线上的元素会导致 \(A\) 和 \(B\) 两个矩阵的同时访问，干扰缓存。而在使用了分块策略之后，这个问题就变得更加突出而复杂。对于对角线上的块，\(A\) 和 \(B\) 在读写的时候会不断地相互驱逐，对角线上的每个元素应该都会带来三次多余的驱逐：\(A\) 的每一行第一个元素的取用会驱逐 \(B\) 的这一行，对角线上 \(B\) 的写会驱逐 \(A\) 的这一行，\(A\) 继续读这一行的元素会驱逐 \(B\) 的这一行……

想要解决这个问题，可以使用 \(8\) 个局部变量来一次性取完 \(A\) 的一整行，再写入 \(B\) 的相应位置，这样就避免了两次驱逐：写 \(B\) 的对角线驱逐 \(A\) 和读 \(A\) 这一行之后的元素又驱逐 \(B\)。虽然无法彻底解决对角线块冲突的问题，但是应该可以做到每行只会冲突一次左右。

void transpose_32x32(int M, int N, int A[N][M], int B[M][N]) {
    for (int ii = 0; ii < 32; ii += 8)
        for (int jj = 0; jj < 32; jj += 8)
            for (int i = ii; i < ii + 8; ++i) {
                int a0 = A[i][jj];
                int a1 = A[i][jj + 1];
                int a2 = A[i][jj + 2];
                int a3 = A[i][jj + 3];
                int a4 = A[i][jj + 4];
                int a5 = A[i][jj + 5];
                int a6 = A[i][jj + 6];
                int a7 = A[i][jj + 7];
                B[jj][i] = a0;
                B[jj + 1][i] = a1;
                B[jj + 2][i] = a2;
                B[jj + 3][i] = a3;
                B[jj + 4][i] = a4;
                B[jj + 5][i] = a5;
                B[jj + 6][i] = a6;
                B[jj + 7][i] = a7;
            }
}

最终结果：

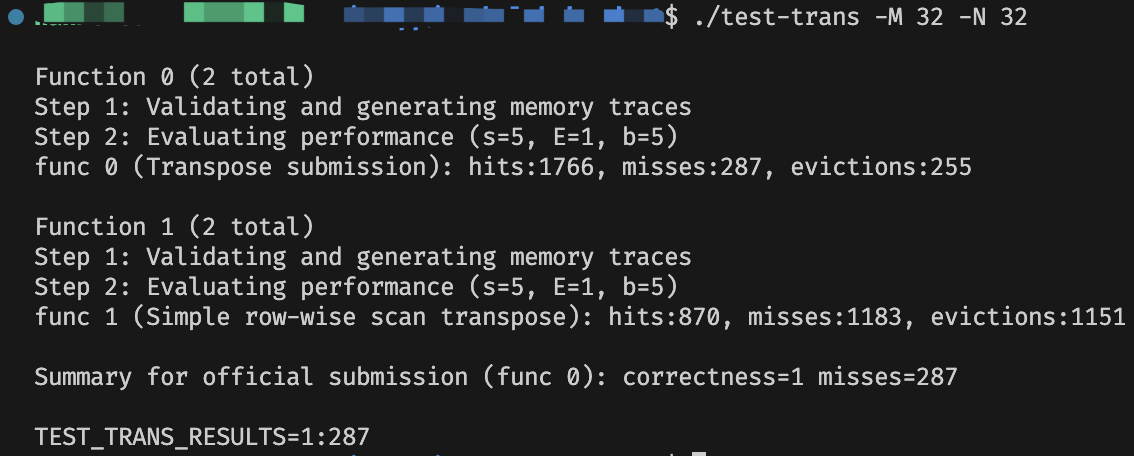
\(64\times 64\)

\(64\times 64\) 的矩阵转置和前一个版本最大的区别就是，原本一行只有 \(4\) 个块，现在一行有了 \(8\) 个块，相应地，原本可以做到 \(8\) 行的不冲突，现在只能做到 \(4\) 行了。

这样就导致，原本 \(8\times 8\) 的分块是很天然的，现在天然的分块应该是 \(4\times 8\) 了，但是这样的分块不利于转置，因为转置只有在一个方方正正的块中才方便。

于是可以想到缩小为 \(4\times 4\) 的块。然而这样做虽然很简单，但是并不能获得满分。

那么我们可以怎么优化呢？

考虑到我们在用 \(4\times 4\) 的块进行转置的时候，其实缓存也会存放右边的 \(4\times 4\) 的块。如图，我们不妨将这块缓存利用起来。首先，我们将一个 \(8\times 8\) 的区域划分为 \(4\) 个 \(4\times 4\) 的小区域，在 \(A\) 矩阵中依次编号为 I, II, III, IV。

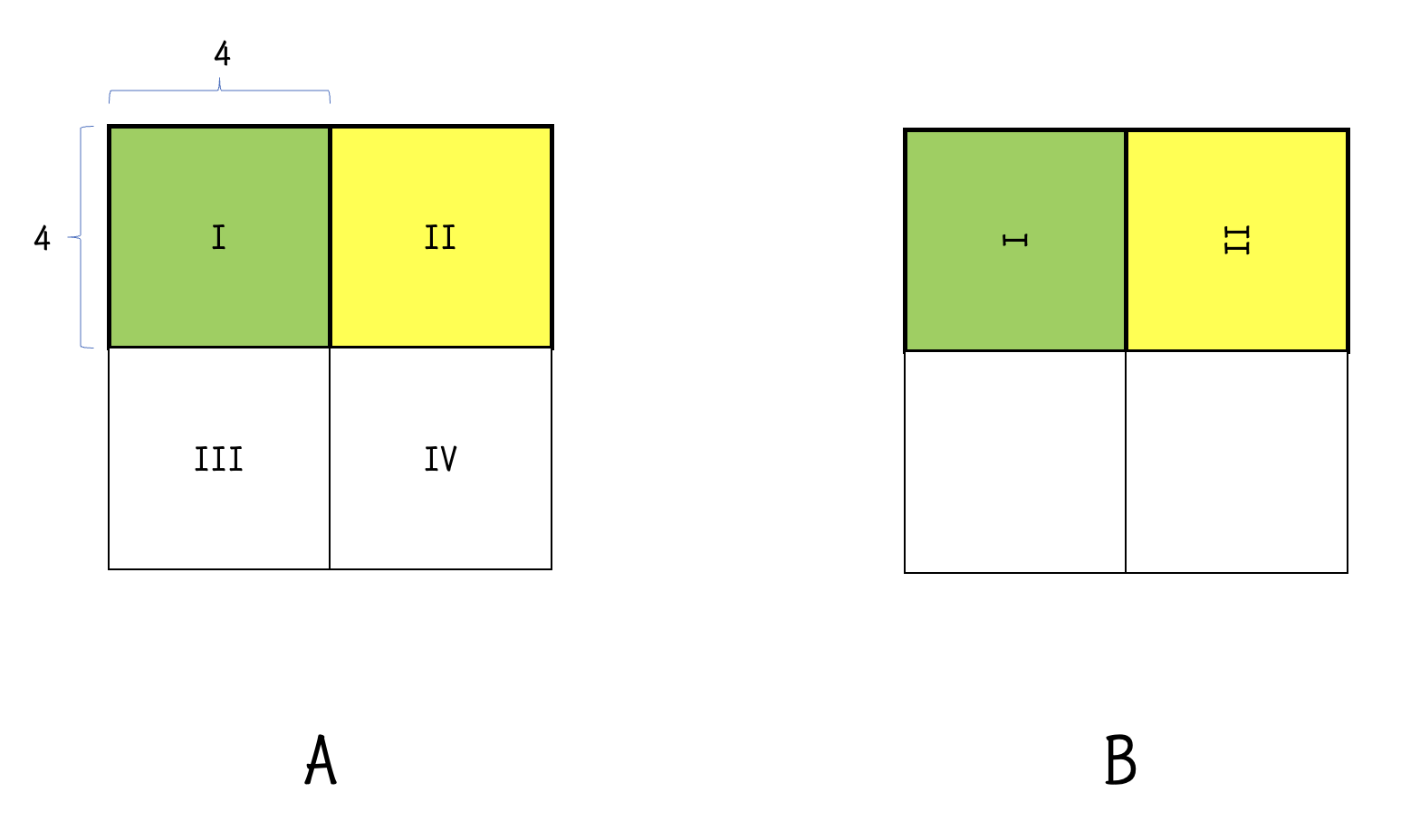
在一开始，我们将 I 区域的转置做完，这个时候，\(A\) 的 II 区域和 \(B\) 矩阵的原本应该存放 III 的区域都已经进入缓存了。因此，我们可以利用这个缓存，将 \(A\) 矩阵的 II 区域的转置先放进 \(B\) 矩阵中原本应该放 III 的区域中，为了方便我们暂时称 \(B\) 的这个区域为 II' 区域。

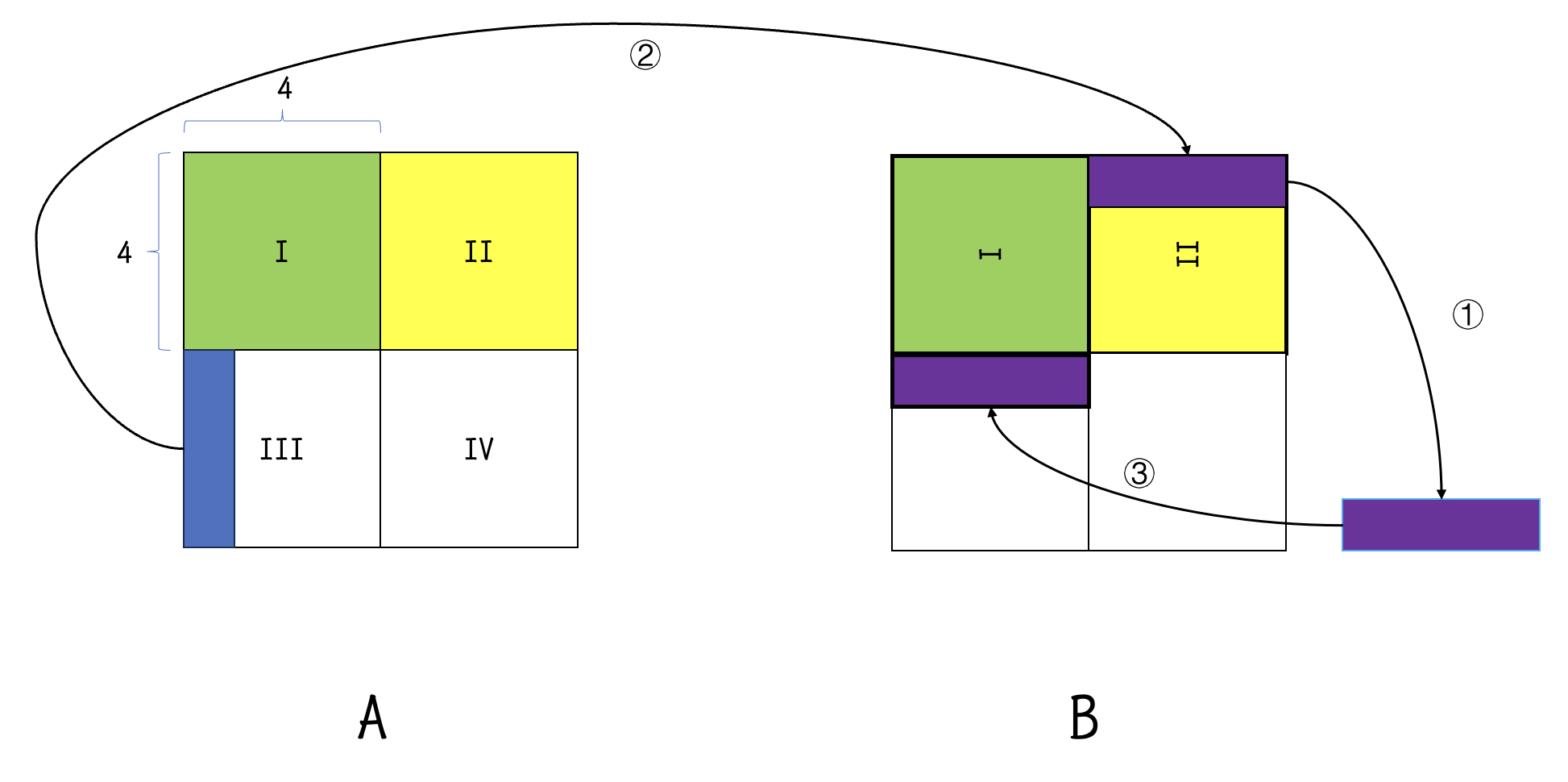
接下来，我们考虑如何将 B 中 II' 区域的一行放进 III 区域的同时，将 A 中 III 区域的转置正确放进 B 的 II' 区域，且不带来不必要的驱逐。如图，我们先将 II' 区域中的一小行复制到临时变量中，然后从 \(A\) 矩阵的 III 区域复制一列到 II‘ 区域的一小行中。复制完成后，我们在将临时变量中取出的一小行放到 B 真正的 II 区域的对应位置。这个过程中，II' 区域这一行将被驱逐，真正的 II 区域中这一行将被缓存，没有重复地驱逐再缓存再驱逐任何一行。

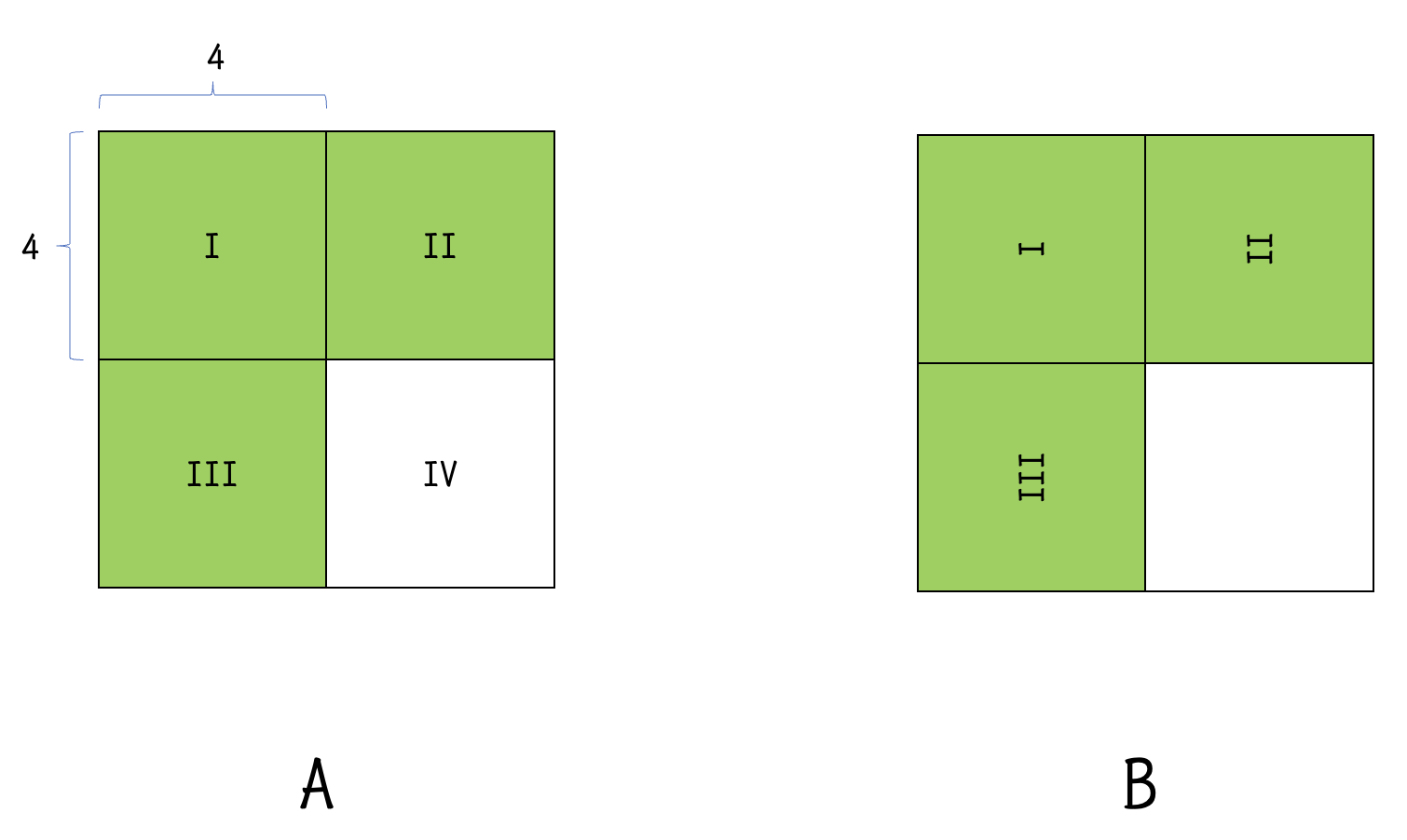
结束后，就只剩下了 IV 区域还没有完成转置，而这个转置过程显然不难，和 I 区域相同的方法即可。

最终代码：

void transpose_64x64(int M, int N, int A[N][M], int B[M][N]) {
    int a0, a1, a2, a3, a4, a5, a6, a7;
    for (int ii = 0; ii < N; ii += 8)
        for (int jj = 0; jj < M; jj += 8) {
            for (int i = ii; i < ii + 4; ++i) {
                a0 = A[i][jj + 0];
                a1 = A[i][jj + 1];
                a2 = A[i][jj + 2];
                a3 = A[i][jj + 3];
                a4 = A[i][jj + 4];
                a5 = A[i][jj + 5];
                a6 = A[i][jj + 6];
                a7 = A[i][jj + 7];
                B[jj + 0][i] = a0;
                B[jj + 1][i] = a1;
                B[jj + 2][i] = a2;
                B[jj + 3][i] = a3;
                B[jj + 0][i + 4] = a4;
                B[jj + 1][i + 4] = a5;
                B[jj + 2][i + 4] = a6;
                B[jj + 3][i + 4] = a7;
            }
            for (int j = jj; j < jj + 4; ++j) {
                a0 = B[j][ii + 4];
                a1 = B[j][ii + 5];
                a2 = B[j][ii + 6];
                a3 = B[j][ii + 7];
                B[j][ii + 4] = A[ii + 4][j];
                B[j][ii + 5] = A[ii + 5][j];
                B[j][ii + 6] = A[ii + 6][j];
                B[j][ii + 7] = A[ii + 7][j];
                B[j + 4][ii + 0] = a0;
                B[j + 4][ii + 1] = a1;
                B[j + 4][ii + 2] = a2;
                B[j + 4][ii + 3] = a3;
            }
            for (int i = ii + 4; i < ii + 8; ++i) {
                a0 = A[i][jj + 4];
                a1 = A[i][jj + 5];
                a2 = A[i][jj + 6];
                a3 = A[i][jj + 7];
                B[jj + 4][i] = a0;
                B[jj + 5][i] = a1;
                B[jj + 6][i] = a2;
                B[jj + 7][i] = a3;
            }
        }
}

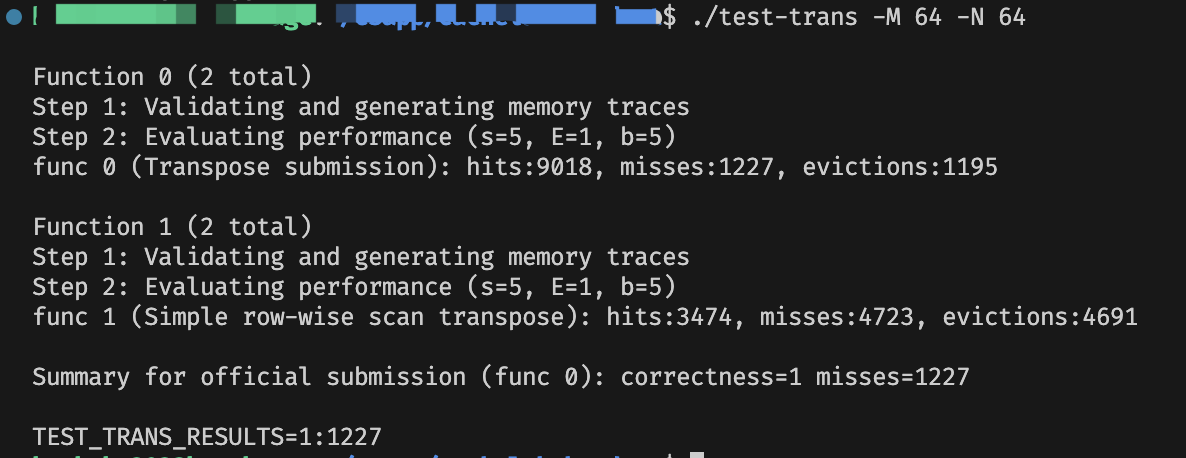
最终的不命中数是 \(1227\)，可以通关了。

\(61 \times 67\)

最后一题是 \(61\) 和 \(67\)，因为不是方方正正的正方形，所以很难直接分析分块的方法。

所幸这个任务的限制很宽松，很多方法都可以通过这个题目。

一种很有用的方法是直接枚举块大小，每一种都试一遍，很快就能找到可以通过的程序了。

我是直接在 \(8\times 8\) 分块的版本上修改了一下对角线处理的版本，加了边界判断，然后就可以通过要求了。

void transpose_61x67(int M, int N, int A[N][M], int B[M][N]) {
    int a0, a1, a2, a3, a4, a5, a6, a7;
    for (int ii = 0; ii < N; ii += 8)
        for (int jj = 0; jj < M; jj += 8)
            for (int i = ii; i < ii + 8 && i < N; ++i) {
                if (jj + 0 < M) a0 = A[i][jj];
                if (jj + 1 < M) a1 = A[i][jj + 1];
                if (jj + 2 < M) a2 = A[i][jj + 2];
                if (jj + 3 < M) a3 = A[i][jj + 3];
                if (jj + 4 < M) a4 = A[i][jj + 4];
                if (jj + 5 < M) a5 = A[i][jj + 5];
                if (jj + 6 < M) a6 = A[i][jj + 6];
                if (jj + 7 < M) a7 = A[i][jj + 7];
                if (jj + 0 < M) B[jj][i] = a0;
                if (jj + 1 < M) B[jj + 1][i] = a1;
                if (jj + 2 < M) B[jj + 2][i] = a2;
                if (jj + 3 < M) B[jj + 3][i] = a3;
                if (jj + 4 < M) B[jj + 4][i] = a4;
                if (jj + 5 < M) B[jj + 5][i] = a5;
                if (jj + 6 < M) B[jj + 6][i] = a6;
                if (jj + 7 < M) B[jj + 7][i] = a7;
            }
}

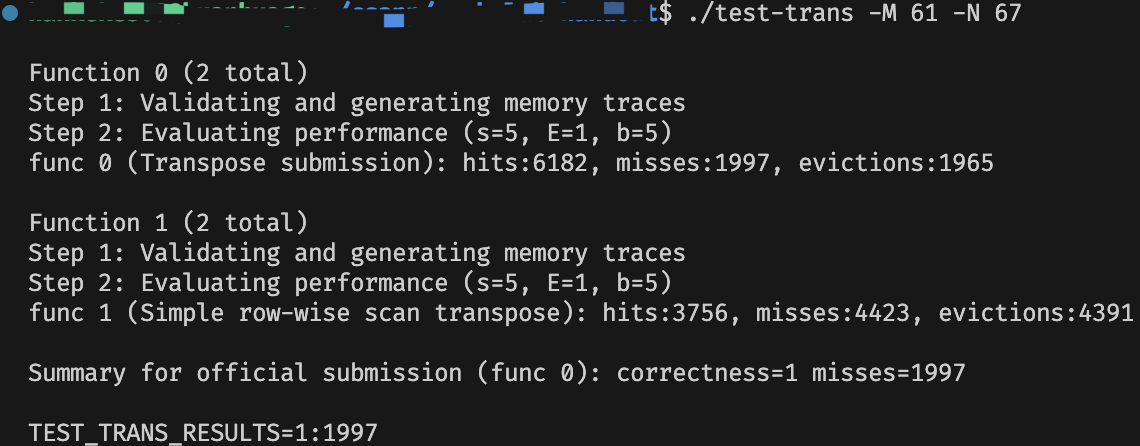
成功贴着线过了这个任务。ヾ(^▽ヾ)

程序

程序太长了就不直接贴上来了，可以点击这个 链接 下载！

得分

贴一下总分的图。