CMU 15-751 CS Theory Toolkit Lecture Lecture 3 - Factorials & Binomial Coefficients

CMU 15-751 课程第三课笔记。

接上回 CMU15-751-2。

同样照抄参考了 Lecture Note。

今天学习的是阶乘和二项式系数的渐进分析，这两种的出现频率非常高，因此我们很有必要熟悉他们的渐进方法。这也是我们做更多渐进分析的练习的机会。

阶乘（Factorials）

\(n! = 2^{\Theta(n\log n)}\)

阶乘我们非常熟悉，\(n! = n(n-1)(n-2)\dots 2\cdot 1 = \prod_{i=1}^n i\)。

那我们如何分析 \(n!\) 的渐进性呢？

首先，我们显然有

\[\begin{aligned} n! &= n(n-1)(n-2)\dots 2\cdot 1\\ &\leq n\cdot n\cdots n \cdot n = n^n \end{aligned} \]

这是 \(n!\) 我们可以确定的一个上界，尽管这个上界可以说宽松得过分。

想要计算 \(n!\) 的下界，我们可以只取前 \(\lceil\frac n2\rceil\) 项，对这些项应该都大于 \(\frac n2\)，对它们都取 \(\lceil\frac n2\rceil\) 的下界，得到

\[\begin{aligned} n! &= n(n-1)(n-2)\dots 2\cdot 1\\ &\geq \lceil\frac n2\rceil\cdot\lceil\frac n2\rceil\cdots\lceil\frac n2\rceil\quad (\lceil\frac n2\rceil\text{times})\\ &= \left(\lceil\frac n2\rceil\right)^{\lceil\frac n2\rceil} \geq \left(\frac n2\right)^{n / 2} \end{aligned} \]

上面的讨论是建立在 \(n\) 是偶数的基础上的，但是在 \(n\) 是奇数的时候这也是成立的，这很容易看出来。

这样，我们就得到了一个仍然不宽松的下界，且把上下界都统一为 \(n^n\) 的形式。

但是我们如何比较 \(n!\) 的上下界呢？即使形式类似，\(\left(\frac n2\right)^{n / 2}\) 和 \(n^n\) 的大小实际上也相差甚远。

对于这样的很大很长的连乘式，对它们不断取对数是一个很常用的做法，因为这样我们就可以把底数大小、连乘次数这些难以解决的东西变成对数下的常数。

因此，我们得到

\[\frac n2\ln\left(\frac n2\right) \leq \ln(n!) \leq n\ln n \]

因此，这里的 \(\ln(n!)\) 的上下界都可以统一为 \(\Theta(n\log n)\)。

于是我们就得到了 \(n! = 2^{\Theta(n\log n)}\)。

当然，这个结果过于宽松，我们不会满意于这个结果。让我尝试获得更精确的结果。

\(\ln(n!) \sim n\ln n\)

通过泰勒公式，我们可以得到：

\[\begin{aligned} e^x &= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots\\ &\geq \frac{x^n}{n!},\quad \forall x \geq 0 \end{aligned} \]

我们令 \(x = n\)，则可以得到 \(n! \geq \frac{x^n}{e^n} = \left(\frac ne\right)^n\)。

这是一个非常优秀的下界，我们将之与之前得到的上界连在一起便可以得到 \(\left(\frac ne\right)^n \leq n! \leq n^n\)。于是

\[n\ln\left(\frac ne\right) = n\ln n - n \leq \ln(n!) \leq n\ln n \]

于是我们就得到了 \(\ln(n!) \sim n\ln n\)。

这是一个非常优美的形式，但是实际上这个界限还是非常宽松——这仅仅是一个对于 \(\ln(n!)\) 的优秀渐进，对于 \(n!\) 本身仍然是一个很大的范围，我们希望知道 \(n!\) 是离 \(\left(\frac ne\right)^n\) 更接近还是距离 \(\left(\frac n1\right)^n\) 更接近。

\(n! \approx \frac{n^n}{e^n}\)

为了解决这个问题，我们可以设出分式的分母。令 \(n! = \frac{n^n}{f(n)}\)，即 \(f(n) = \frac{n^n}{n!}\)。我们只需要关心 \(f(n) \to 1\) 还是 \(f(n)\to e^n\)，也就是 \(\frac{f(n+1)}{f(n)}\to 1\) 还是 \(\frac{f(n+1)}{f(n)}\to e\)。

\[\begin{aligned} \frac{f(n+1)}{f(n)} &= \frac{(n+1)^{n+1} / n^n}{(n+1)! / n!}\\ &= \frac{(n+1)^{n}}{n^n}\\ &= (1 + \frac 1n)^n \end{aligned} \]

根据微积分的基本知识，我们知道这个式子的极限是 \(e\)。（实际上，这也是 \(e\) 的定义之一，或者也可以通过 \(1 + \frac 1n \approx e^{1/n}\) 来理解）

于是我们就得到了 \(f(n) \approx e^n\)，那么对于很大的 \(n\)，我们就可以有 \(n! \approx \frac{n^n}{e^n}。\)

\(n! = \Theta(\frac{n^n}{e^n}\sqrt n)\)

模仿上一个 Lecture 中我们求调和数的渐进性的方法，我们可以用积分发来更精确地计算 \(n!\) 的渐进。

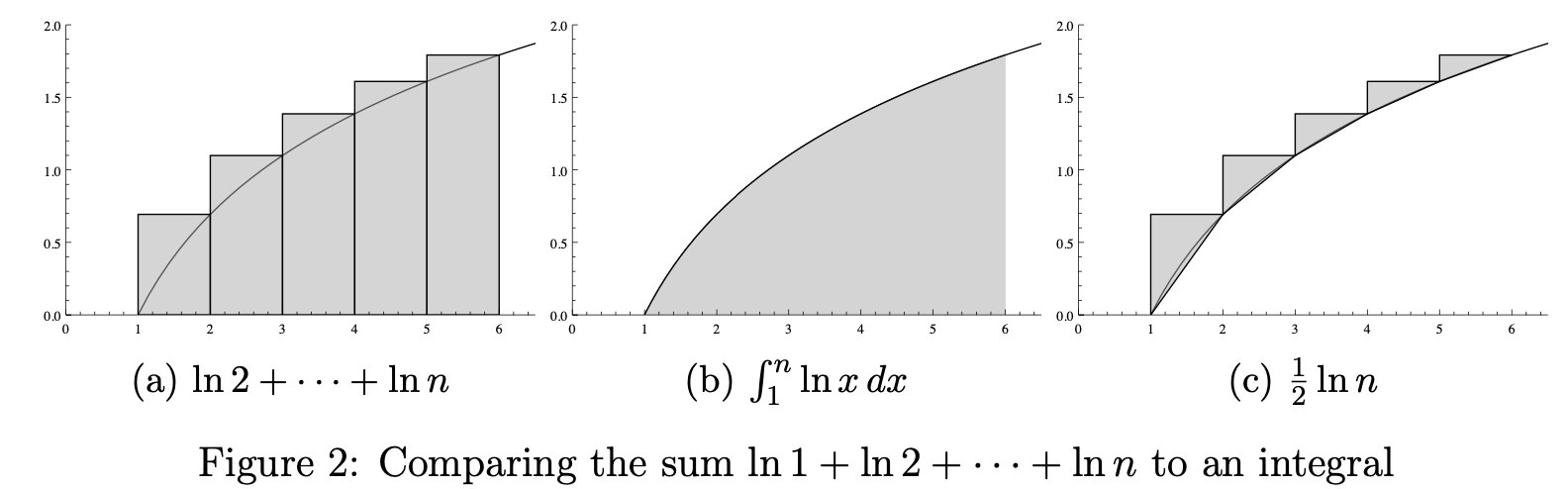
我们知道 \(\ln(n!) = \ln 1 + \ln 2 + \ln 3 + \dots + \ln n\)，其中 \(\ln 1 = 0\)，因此我们可以用 \(\int_1^n \ln t\ \mathrm dt\) 来接近 \(\ln(n!)\)。

如上面的图 (a) 所示，我们可以得到

\[\begin{aligned} \ln(n!) &\geq \int_1^n \ln t\ \mathrm dt\\ &= t\ln t - t \big|_1^n\\ &= n\ln n - n + 1 \end{aligned} \]

这样我们就算出了 \(\ln(n!)\) 的上限。

我们很清楚地知道我们这里的积分多算了哪一块。我们可以通过把每一个矩形左上角的三角形加回来，如图 (c) 所示，来弥补这个多算的部分——但是这样会导致有若干的小薄条没有被计算，因此我们得到的是 \(\ln(n!)\) 的下限。

图 (c) 中的每一个小薄条，都是底为 \(1\)，高为 \(\ln n - \ln(n-1)\) 的直角三角形。这些直角三角形的面积和很容易计算，它们的高之和显然就是 \(\ln 2 - \ln 1 + \ln 3 - \ln 2 + \dots + \ln n - \ln(n-1) = \ln n\)，因此它们的面积和就是 \(\frac 12 \cdot 1 \cdot \ln n = \frac 12 \ln n\)。

于是我们得到

\[n\ln n - n + 1 \leq \ln(n!) \leq n\ln n - n + \frac 12\ln n + 1 \]

对两边做 \(\exp\) 运算，得到

\[\frac{n^n}{e^n}\cdot e \leq n! \leq \frac{n^n}{e^n} \cdot \sqrt n \cdot e \]

这样我们就把 \(n! \approx \frac{n^n}{e^n}\) 推进到了一个更紧的范围。这个形式也可以写成 \(n! = \tilde\Theta\left(\frac{n^n}{e^n}\right)\)。

但是这个结果我们仍然不满意。我们想要知道除了 \(\frac{n^n}{e^n}\) 这个因式之外，剩下的那个因式到底是 \(\Theta(1)\) 还是 \(\Theta(\sqrt n)\)。

我们知道，我们刚刚在计算 \(\ln(n!)\) 的上界时，求得的结果只比真正的值多了若干个小薄片。那么我们要想办法把这个小薄片的面积减去。

直接计算当然不好算，但是我们可以想办法去接近。我们可以再 \(y = \ln x\) 的曲线上，每一次都从第 \(i\)（\(i\) 从 \(2\) 开始编号）个小薄条的右上角 \((n, \ln n)\) 做一个切线，与 \(x = n-1\) 这条直线的交点，以及 \((n-1, \ln(n-1))\) 这三个点构成一个三角形。这个三角形的面积显然会比小薄条的面积大，因此减去后就可以得到一个更紧密的下界。

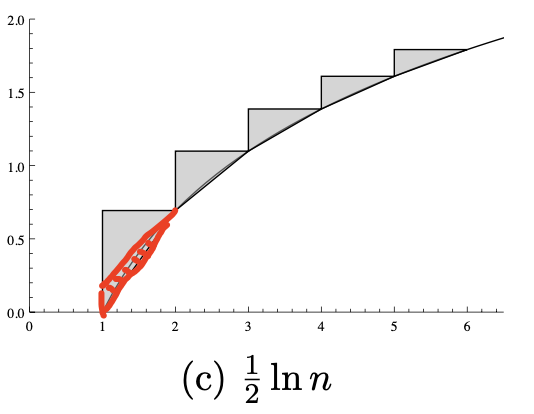
我们知道 \((n, \ln n)\) 点的切线斜率是 \(\frac 1n\)，因此交点的 \(y\) 坐标是 \(\ln n - \frac 1n\)，三角形的底就是 \(\ln n - \ln(n-1) - \frac 1n\)。于是小三角形的总面积就是

\[\begin{aligned} &\frac 12\sum_{i=2}^n \left(\ln n - \ln(n-1) - \frac 1n\right)\\ =& \frac 12\sum_{i=2}^n \ln n - \frac 12\sum_{i=1}^{n-1}\ln n - \frac 12\sum_{i=2}^n \frac 1n\\ =& \frac 12(\ln n - H(n) + 1) \end{aligned} \]

其中，\(H(n)\) 是我们上一个 Lecture 的调和数。我们知道 \(H(n) = \ln n + \gamma - O(\frac 1n)\)。因此上式可以写为 \(\frac 12\left( 1 - \gamma + O\left(\frac 1n\right)\right) = \Theta(1)\)。

也就是说

\[n\ln n - n + \frac 12\ln n + 1 - \Theta(1)\leq \ln(n!) \leq n\ln n - n + \frac 12\ln n + 1 \]

即

\[n! = \Theta(\frac{n^n}{e^n}\sqrt n) \]

斯特林公式（Stirling's Formula）

实际上从上面的结论到这个公式还需要做更多的计算。如果真的想要求出这个常数的话再后面的学习中我们可能会遇到。但是这里我们只需要知道

\[n! = \sqrt{2\pi n} \left(\frac ne\right)^n\left(1 \pm O\left(\frac 1n\right)\right) \]

二项式系数（Binomial Coefficients）

当 \(k\) 非常小的时候，\(\binom nk \approx \frac{n^k}{k!}\)

二项式系数我们都很熟悉，\(\binom nk = \frac{n!}{k!(n-k)!} = \frac{n(n-1)\cdots(n-k+1)}{k!}\)。它可以表示从 \(n\) 个不同物品中选出 \(k\) 个的方案数，也可以表示二项式展开得到的系数。

当 \(k\) 很小，也就是 \(k << n\) 时，我们可以得到

\[\begin{aligned} &\frac{n(n-1)\cdots(n-k+1)}{k!}\\ =& \frac{n^k}{k!}\left(1 - \frac 1n\right)\left(1 - \frac 2n\right)\cdots\left(1 - \frac{k-1}n\right)\\ =& \frac{n^k}{k!}P_{k, n}\\ =& \frac{n^k}{k!}\exp\left(-\frac{k^2}{2n}\right) \sim \frac{n^k}{k!}\left(1-\frac{k^2}{2n}\right)\\ \sim& \frac{n^k}{k!} \end{aligned} \]

其中 \(P_{k, n}\) 是我们在之前的生日问题中定义的数。

于是我们得到，当 \(k\) 非常小的时候，\(\binom nk \approx \frac{n^k}{k!}\)。

简单的上下界

实际上，因为 \(n(n-1)\cdots(n-k+1) \leq n^k\)，所以 \(\frac{n^k}{k!}\) 是 \(\binom nk\) 的一个简单的上界，这对任意的 \(k\) 都成立。又因为 \(k! \geq \frac{k^k}{e^k}\)，于是我们可以得到一个工整一些的形式：

\[\binom nk \leq \left(\frac{en}k\right)^k \]

我们也可以求出 \(\binom nk\) 的下界。

我们知道

\[\binom nk = \frac nk\cdot \frac{n-1}{k-1}\cdot\frac{n-2}{k-2}\cdots\frac{n-k+1}{1} \]

因为 \(\frac{n-i}{k-i} \geq \frac nk\)（可以通过 \(\Leftrightarrow nk - ki \geq nk - ni\) 来证明），因此我们可以得到

\[\binom nk \geq \left(\frac nk\right)^k \]

我们惊喜地看到，我们得到的上界和下界仅有一个 \(e^k\) 的因式的差异。这样的渐进对于我们来说往往是足够的，如果我们取一下对数，我们可以得到

\[k\ln\left(\frac nk\right) \leq \ln\binom nk \leq k\ln\left(\frac {en}k\right) = k\ln\left(\frac nk\right) + k \]

也就是 \(\ln \binom nk = \Theta\left(k\ln\left(\frac nk\right)\right)\)。

\(\binom n{pn} \leq 2^{H(p)n}\)

如果我们知道常数 \(p\) 满足 \(0 < p \leq \frac n2, k = pn\)，我们希望能够对于这时的 \(\binom nk\) 能够更好地分析渐进性。

一般来说，这里我们应该使用斯特林公式来求解这个问题，但是让我们先来试着用一些基本的方法求出 \(\binom n{pn}\) 的上界。

我们令 \(V(n, k) = \binom n0 + \binom n1 + \dots + \binom nk\)。这个值可以代表 \(1\) 的个数不多于 \(k\) 的长度为 \(n\) 的不同二进制字符串的数量，也通常被认为半径为 \(k\) 的以 \(00\cdots0\)（\(n\) 个 \(0\)）为中心的「Hamming ball」的数量的容量。这个数在 TCS 中经常出现。

由二项式定理：

\[\begin{aligned} (1 + x)^n &= 1 + \binom n1x + \binom n2x^2 + \dots + \binom nkx^k + \dots + \binom nnx^n\\ &\geq \binom n0 + \binom n1x + \binom n2x^2 + \dots + \binom nkx^k\\ &\geq x^k\cdot V(n, k),\quad\forall0 < x \leq 1 \end{aligned} \]

因此

\[\begin{aligned} V(n, k) &\leq \frac{(1 + x)^n}{x^k} = \frac{(1 + x)^n}{(pn)^k} = \left(\frac{1+x}{x^p}\right)^n\\ &= \left(x^{-p} + x^{1-p}\right)^n = \left(x^{-p} + x^q\right)^n,\quad\forall0 < x \leq 1 \end{aligned} \]

其中，我们令 \(q = 1 - p\)。

通过求导我们可以知道，当 \(x = \frac pq\) 时，\(x^{-p}+x^q\) 取得最小值。这个 \(x\) 会小于等于 \(1\)，因为我们曾假设 \(p \leq \frac 12\)。那么此时

\[\begin{aligned} x^{-p}+x^q &= x^{-p} (1+x) = x^{-p}\left(1 + \frac pq\right)\\ &= x^{-p}\cdot\frac 1q = \left(\frac pq\right)^{-p}\cdot \frac 1q\\ &= \left(\frac qp\right)^{p} \left(\frac 1q\right)^{p}\left(\frac 1q\right)^{q}\\ &= \left(\frac 1p\right)^{p}\left(\frac 1q\right)^{q} \end{aligned} \]

因而

\[\binom n{pn} \leq V(n, pn) \leq \left[\left(\frac 1p\right)^{p}\left(\frac 1q\right)^{q}\right]^n = p^{-pn}q^{-qn} \quad \text{for}\ p\leq \frac 12 \]

如果我们令 \(H(p) = p\log_2\frac 1p + q\log_2\frac 1q\)，这个函数一般被称为二元交叉熵（Binary entropy function），那么上式可以写成

\[\binom n{pn} \leq V(n, pn) = 2^{H(p)n} \]

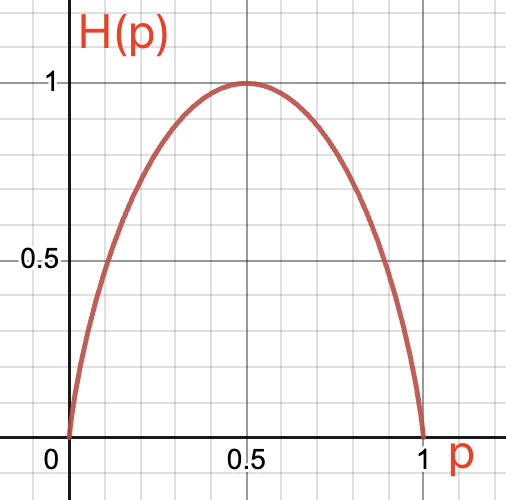
\(\binom n{pn} = \Theta\left(\frac 1{\sqrt n}2^{H(p)n}\right)\)

现在让我们来使用斯特林公式解决这个问题。

\[\begin{aligned} \binom n{pn} &= \frac{n!}{(pn)!(qn)!}\\ & \sim \frac{\sqrt{2\pi n}(n/e)^n}{\sqrt{2\pi n}(pn/e)^{pn}\cdot \sqrt{2\pi n}(qn/e)^{qn}}\\ &= \frac{\sqrt{2\pi n}(n/e)^n}{(2\pi n)(n/e)^n p^{pn}q^{qn}}\\ &= \frac 1{\sqrt{2\pi pq}}\frac 1{\sqrt n}\left[\left(\frac 1p\right)^p\left(\frac 1p\right)^q\right]^n\\ &= \frac 1{\sqrt{2\pi pq}}\frac 1{\sqrt n} 2^{H(p)n} \end{aligned} \]

因此，\(\binom n{pn} = \Theta\left(\frac 1{\sqrt n}2^{H(p)n}\right)\)。

特别的，当 \(p = \frac 12\) 时，\(H(p) = 1\)，因此

\[\frac{\binom n{n/2}}{2^n} \sim \sqrt{\frac 2{\pi n}} = \Theta\left(\sqrt{\frac 1n}\right) \]

也就是说，如果我们抛 \(n\) 枚硬币（\(n\) 是偶数），恰好 \(\frac n2\) 枚硬币正面朝上的概率，大约会趋近于 \(\sqrt{\frac 2{\pi n}} = \Theta\left(\sqrt{\frac 1n}\right)\)。