CMU 15-751 CS Theory Toolkit Lecture 2 - Basic Asymptotics

CMU 15-751 课程第二课笔记。

CS Theory Toolkit at CMU - YouTube

照抄参考了 Lecture Note。

渐进标记（Asymptotic Notation）

我们知道

\[\sum_{i=1}^n i = \frac{n(n+1)}2 = \frac 12 n^2 + \frac 12 n \]

在 \(n\) 很大的时候，平方项这个函数值的影响会更显著。我们可以把这一个特性写作

\[\sum_{i=1}^n i = O(n^2) \]

一般我们说 \(f(x) = O(g(x))\)，表示当 \(x\) 足够大的时候，存在常数 \(C > 0\)，使 \(0 \leq f(x) \leq Cg(x)\)。

更加形式的定义是，\(\exists C, x_0 > 0\)，使得 \(|f(x)| \leq Cg(x), \forall x \geq x_0\)。一般来说，我们研究的函数往往是正数，因此常常写为 \(0 \leq f(x) \leq Cg(x)\)。

上面所说的是 \(x\to \infty\) 时的大 \(O\) 符号的含义。有的时候，这个符号也可以用在 \(x \to 0^+\) 时。那么类似的定义就是 \(\exists C > 0, x_0\)，使得 \(|f(x)| \leq Cg(x), \forall 0 \leq x \leq x_0\)。

一般，被我们叫做 \(n\) 的变量是趋向于 \(\infty\) 的，叫做 \(\varepsilon\) 的变量是趋向于 \(0^+\) 的，因此我们常常省略自变量的趋向。

很多时候 \(O(g(x))\) 可以表示一个满足 \(|f(x)| \leq Cg(x), \forall x \geq x_0\)（也就是上面的定义）的一个匿名函数。这样的写法并不标准，但是经常被使用，例如之前的函数可以计作下面的形式：

\[\begin{aligned} \sum_{i=1}^n i &= \frac 12 n^2 + O(n)\\ &= \frac 12 n^2(1 + O(\frac 1n)) \end{aligned} \]

上面第二行的写法非常直观地体现了函数值的近似答案，以及一个趋近于 \(1\) 的乘法误差。

我们还有一些类似的符号来表示一些不同的函数渐进性：

• \(f(x) = \Omega(g(x))\) 代表 \(\exists C > 0, x_0\)，使得 \(f(x) \geq Cg(x), \forall x \geq x_0\)。
• \(f(x) = \Theta(g(x))\) 代表 \(f(x) = O(g(x))\) 且 \(f(x) = \Omega(g(x))\)，即 \(\exists C_1, C_2 > 0, x_0\)，使得 \(C_1g(x) \leq f(x) \leq C_2g(x)\)。
• \(f(x) = o(g(x))\) 表示 \(\frac{f(x)}{g(x)} \to 0\)。
• \(f(x) = \omega(g(x))\) 表示 \(\frac{f(x)}{g(x)} \to \infty\)。
• \(f(x) \leq \rm{poly}(g(x))\) 代表 \(f(x) = g(x)^{O(1)}\)，即 \(f(x)\) 被限制在 \(g(x)\) 的常数次幂下。
• \(f(x) = \tilde O(g(x))\) 代表 \(f(x) \leq g(x)\cdot \mathrm{poly}(\log g(x))\)。这样的限制成为 lazy bound。例如，\(n^2\log^3n = \tilde O(n^2)\)，\(n^5\cdot 3^n = \tilde O(3^n)\)。需要注意的是，\(n^5\cdot 3^n\) 不能计作 \(\tilde O(2^n)\)。
  • 如果 \(x\to 0^+\)，那么其含义与上面不同，此时 \(f(x) = g(x)\cdot\mathrm{poly}(\log 1 / {g(x)})\)。
  • \(f(x) = \tilde\Omega(g(x))\) 代表 \(f(x) \geq \frac{g(x)}{\mathrm{poly}(g(x))}\)。例如，\(\frac{n^3}{\log^2n} = \tilde\Omega(n^3)\)。
• \(f(x) \sim g(x)\) 代表 \(\frac{f(x)}{g(x)} \to 1\)。这种形式可以等价地写成 \(f(x) = g(x)(1 \pm o(1))\)，在证明中常常使用这样的形式。比如 \(\sum_{i=1}^n i = \Theta(n^2)\)，我们可以将之写成更明确的 \(\sum_{i=1}^n i \sim \frac 12 n^2\)。

显然，我们使用这些符号来表示一个函数渐进的界限，是为了函数值的变化更容易分析。因此，\(g(n)\) 这样的函数就不能太复杂。对于这样的函数的取用，我们有一些约定俗成的规则，如果它应该是下面几种情形之一，或者它们的乘积，我们就称之为标准形式（不是正式术语）：

1. 常数（如 \(3, \sqrt{2\pi}\)）；
2. \(\log n\) 的常数次幂（如 \(\log n, \sqrt{\log n}, \frac 1{\log n}\)），一般来说我们用 \(\ln\) 表示 \(\log_e\)，\(\lg\) 表示 \(\log_2\)，如果只有 \(\log\) 则代表我们不关心其底数；
3. \(n\) 的常数次幂（如 \(n, n^{5.3}\)）；
4. 指数函数（如 \(2^n, e^{-n}, 2^{n/2}\)）；
5. \(n^{cn}\)，其中 \(C\) 为常数。

比如，\(g(n) = n^5\cdot 3^n\)、\(g(n) = 6n^2\sqrt{\log n}\) 和 \(g(n) = \sqrt{2\pi n}(\frac ne)^n\) 都是这里所说的标准形式，后者就是我们一会儿就会提到的斯特林公式中 \(n!\) 的渐进。

以上五种形式的函数，每一种都满足在渐进性上小于下一种函数，即使对其做上任意正数次幂。比如 \((\ln n)^{100} = o(n^{1/10})\)，\(100n^{50} = o(1.1^n)\)。

这些并不是我们可能会用到的渐进函数的全部集合，比如 \(O(\log\log n)\) 也是我们常用到的，但是我们在处理一个复杂的函数时，可以首先尝试这些标准形式的乘积。

调和数（The Harmonic Number）

调和数 \(H_n = 1 + \frac 12 + \frac 13 + \dots + \frac 1n\)。

首先让我们用一些并不精确的方法估计一下这个函数的渐进性。

我们将每一个 \(\frac 1i\) 缩放到其最接近的两个 \(2\) 的整次幂，便可以得到

\[\begin{aligned} H_n &\leq 1 + \frac 12 + \frac 12 + \frac 14 + \frac 14 + \frac 14 + \frac 14 + \frac 18 + \dots\\ &\leq \lfloor\log_2 n\rfloor + 1 \end{aligned} \]

\[\begin{aligned} H_n &\geq 1 + \frac 12 + \frac 14 + \frac 14 + \frac 18 + \frac 18 + \frac 18 + \frac 18 + \frac 1{16} + \dots\\ &\leq \frac 12\lceil\log_2 n\rceil + 1 \end{aligned} \]

所以我们便可以得到 \(H_n = \Theta(\log n)\)。一般来说，我们得到这个结果就可以了，但是如果我们想要得到更精确的结果，便可以使用积分来近似。如下图，其中曲线为 \(y = \frac 1x\)，(b) 中的阴影部分是 \(y = \frac 1x\) 和 \(x\) 轴所夹部分在 \([1, n]\) 上的面积，即 \(\int_1^n \frac 1x \mathrm{d}x\)。图 (a) 和图 (c) 分别是调和数的两种近似方法。

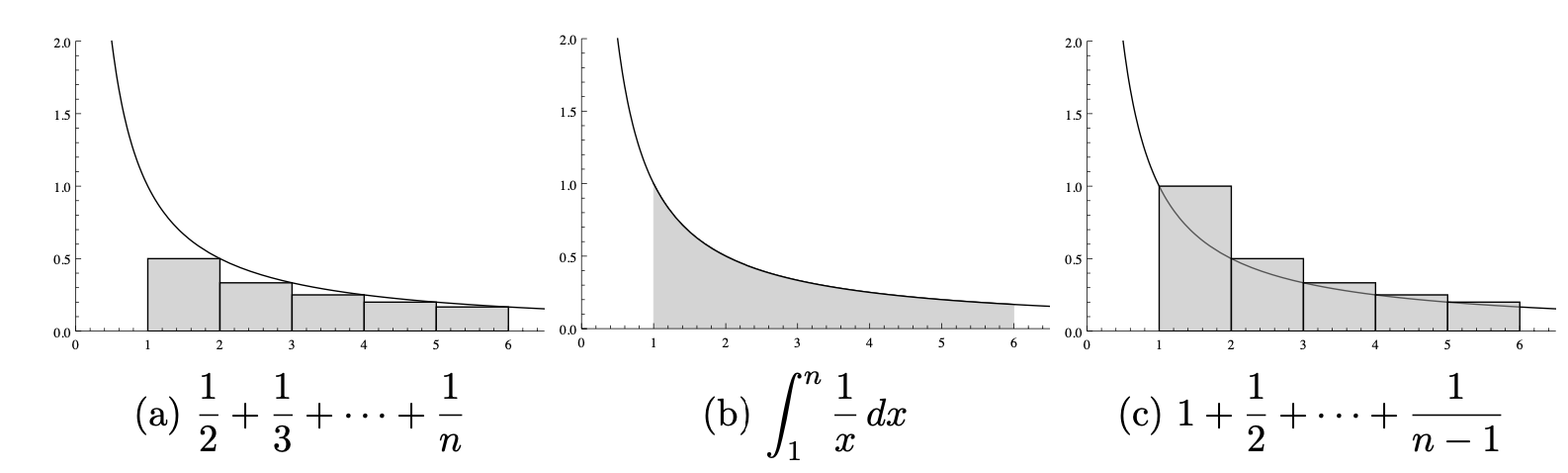
由此我们可以得到两个结论：

\[\begin{aligned} H_n &\leq 1 + \int_1^n \frac 1x \mathrm{d}x\\ &= 1 + \ln x\big |_1^n = 1 + \ln n \end{aligned} \]

\[\begin{aligned} H_n &\geq \int_1^{n+1} \frac 1x \mathrm{d}x\\ &= \ln x\big |_1^{n+1} = \ln (n+1) \end{aligned} \]

于是我们可以得到 \(\ln n \leq \ln(n+1)\leq H_n \leq \ln n + 1\)。

到这里，我们已经可以确定 \(H_n \sim \ln n\)。如果我们想要比较用 \(\ln n\) 代替 \(\ln(n+1)\) 和 \(1 + \ln n\) 时的误差，可以将之写成 \(\ln n(1 \pm o(1))\) 的形式：

\[\begin{aligned} 1 + \ln n &= \ln n (1 + \frac 1{\ln n})\\ \ln(n+1)&= \ln(n(1 + \frac 1n))\\ &= \ln n + \ln(1 + \frac 1n)\\ &= \ln n + \frac 1n \pm O(\frac 1{n^2})\\ &= \ln n(1 + \frac 1{n\ln n} \pm O(\frac 1{n^2\ln n})) \end{aligned} \]

其中 \(\ln(n+1)\) 的第二步来源于 \(\ln(1 + x)\) 的泰勒级数：

\[\ln(1 + x) = x - \frac{x^2}2 + \frac{x^3}3 - \frac{x^4}4 + \dots(-1 < x \leq 1) \]

于是我们可以得到 \(\ln(1+x) = x \pm O(x^2)\sim x(x\to 0)\)。所以对于 \(\ln(1 + \frac 1n)\)，\(\frac 1n \to 0^+\)，我们也有 \(\ln(1 + \frac 1n) = \frac 1n \pm O(\frac 1{n^2})\)。

事实上，如果我们用 \(\ln n\) 来代替 \(H_n\)，这个误差大约会趋近于 \(\frac 12\) 左右的值。这个值我们一般写作 \(\gamma \approx 0.577\)，被称为欧拉常数，\(H_n = \ln n + \gamma - O(\frac 1n)\).

渐进技巧（Asymptotic Tricks）

泰勒级数（Taylor Series）

除了上面的对很小的 \(x\) 有 \(\ln(1 + x)\approx x\)，还有很多类似的结论，比如对于很小的 \(x\) 有 \(e^x \approx 1 + x\)。

事实上，在泰勒级数中，\(e^x = 1 + x + \frac{x^2}2 + \frac{x^3}3 + \frac{x^4}4 + \dots(\forall x \in \R)\)。因而我们可以说 \(e^x = 1 + x + O(x^2)(x\to 0)\)。实际上，在 \(-1 \leq x \leq 1\) 时，这个 \(O(n^2)\) 的误差项被严格包含在 \([0, x^2]\) 的区间内。

除此之外，还有更多常用的泰勒级数结论：

\[\begin{aligned} \frac 1{1 - \varepsilon} &= 1 + \varepsilon + \varepsilon^2 + \varepsilon^3 + \dots\\ &= 1 + \varepsilon \pm O(\varepsilon^2) \end{aligned} \]

实际上，这也可以由 \(\frac 1{1 - \varepsilon} \approx \frac 1{e^{-\varepsilon}} = e^{\varepsilon}\) 印证。

\[\begin{aligned} \sqrt{1 + \varepsilon} &= 1 + \frac\varepsilon 2 - \frac{\varepsilon^2}8 + \frac{\varepsilon^3}{16}-\dots\\ &= 1 + \frac\varepsilon 2 \pm O(\varepsilon^2) \end{aligned} \]

同样，这也可以由 \((1 + \varepsilon)^{1/2} \approx (e ^ \varepsilon)^{1/2} = e^{\varepsilon/2} \approx 1 + \frac\varepsilon 2\) 印证。

一些例题

\(\sqrt{n+1} - \sqrt n\) 的渐进？

\[\begin{aligned} \sqrt{n+1} &= \sqrt{n(1 + \frac 1n)}\\ &= \sqrt n \sqrt{1 + \frac 1n}\\ &= \sqrt n(1 + \frac 1{2n} \pm O(\frac 1{n^2}))\\ \sqrt{n+1} - \sqrt n &= \sqrt n(1 + \frac 1{2n} \pm O(\frac 1{n^2}) - 1)\\ &= \frac 1{2\sqrt n} \pm O(n^{1.5})\\ &= \frac 1{2\sqrt n}(1 \pm O(\frac 1n)) \sim \frac 1{2\sqrt n} \end{aligned} \]

\(\log_2\frac 1{\frac 12 - \varepsilon}\)？

\[\begin{aligned} \log_2\frac 1{\frac 12 - \varepsilon} &= \log_2\frac 2{1 - 2\varepsilon}\\ &= \log_2 2 - \log_2(1-2\varepsilon)\\ &= 1 - \frac{\ln(1 - 2\varepsilon)}{\ln 2}\\ &= 1 - \frac 1{\ln 2} (-2\varepsilon \pm O(\varepsilon^2))\\ &= 1 + \frac 2{\ln 2}\varepsilon \pm O(\varepsilon^2) \end{aligned} \]

反函数

假设我们有 \(y = x\ln x, x\geq 1\)。这是一个单调递增的函数，所以它一定有反函数。求 \(x = f(y)\) 的渐进？

根据定义 \(y = \tilde\Theta(x)\)，即除了一些很小的因式，\(y\) 基本上是和 \(x\) 呈线性关系的。因此大概会有 \(\ln x \approx \ln y\)。实际上也就是，

\[\begin{aligned} \ln y &= \ln x + \ln\ln x \sim \ln x\quad(x\to \infty, y\to \infty) \end{aligned} \]

那么 \(\ln x\) 和 \(\ln y\) 是渐进相等的，我们就可以做一些替换：

\[y = x\ln x \sim x \ln y\\ \Rightarrow x\sim \frac y{\ln y} \]

\(t^2\log t = n^3\)，求 \(t\) 的渐进性。

\[\begin{aligned} &2\log t + \log\log t = 3\log n\\ \Rightarrow& \log n = \frac 23\log t + \frac 13 \log\log t\sim \frac 23\log t\\ \Rightarrow& \log t = \Theta(\log n)\\ \Rightarrow& t^2\Theta(\log n) = n^3\\ \Rightarrow& t = \Theta(\sqrt{\frac{n^3}{\log n}}) = \Theta(\frac{n^{3/2}}{\sqrt{\log n}}) \end{aligned} \]

含参最小化

如果一个算法的运行时间是 \(O(\frac{n^3}t) + O(t\log t)\)，\(t\) 可以取任意值。那么应该选择怎样的 \(t\) 使运行时间最低呢？

我们知道，\(\max(a, b) \leq a + b \leq 2\max(a, b)\)。因此，如果我们不太在意常数因子，我们可以认为 \(a + b \approx \max(a, b)\)。

于是，如果我们想要最小化原式两个部分的和，我们的任务等价于要同时让这两个部分都变小。

考虑到，两个子式随着 \(t\) 的增加，一个单调增，一个单调减（大概如上图所示），我们很容易发现当两个部分相等的时候，它们的最大值才是最小的。

因此我们只需要让 \(\frac{n^3}t = t\log t\)。这是我们刚刚才解决过的问题，其答案是 \(t = \Theta(\frac{n^{3/2}}{\sqrt{\log n}})\)。

则 \(\log t = \Theta(\log n)\)。代入原式，得到总的时间为 \(O(n^{3/2}\sqrt{\log n})\)。

实际上，上面的过程可不能并不严谨，但是对于这样的问题我们一般并不需要形式化地证明，只需要会求出这样的 \(t\) 值即可。

生日悖论（Birthday Paradox）

生日悖论是指在不少于 \(23\) 个人中至少有两人生日相同的概率大于 \(50\%\)，这听上去与一般直觉相抵触而已，所以常常被戏称为“悖论”。生日悖论的衍生版本经常在 TCS 中出现。

我们换一种方式理解这个问题：将 \(n\) 个球均匀随机地扔进 \(m( = 365)\) 个桶中，设没有发生冲突，即所有的球都在不同的桶中的概率为 \(P_{n, m}\)（这里假设 \(n \leq m\)，因为 \(n > m\) 时一定会发生冲突）。我们很容易写出 \(P_{n, m}\) 的计算式：

\[P_{n, m} = 1\cdot (1 - \frac 1m)(1 - \frac 2m)\cdots (1 - \frac{n-1}m) \]

对这样的很多项的乘积做渐进分析，我们常常会在两边取 \(\ln\) 来解决。但是这样我们保留乘积，使用 \(e^x\approx 1 + x\) 来替换每一项。

通过之前泰勒级数或者别的方法，我们很容易知道 \(1 - x \leq e^{-x}, \forall x > 0\)。所以我们得到

\[\begin{aligned} P_{n, m} &\leq \exp(0)\exp(-\frac 1m)\exp(-\frac 2m)\cdots\exp(-\frac{n-1}m) \\ &= \exp\left(-\frac 1m(1 + 2 + \dots + (n-1))\right)\\ &= \exp\left(-\frac{n(n-1)}{2m}\right) \end{aligned} \]

这样，我们就得到了 \(P_{n, m}\) 的上限，通过这个上界我们已经可以估算和验证生日问题的结论了。当然，我们同样可以求出它的下限。

类似于 \(1 - \varepsilon \leq e^{-\varepsilon}\) 的上界，我们也有它的下界公式：\(\exists C, 1 - \varepsilon \geq \exp(-\varepsilon - C\varepsilon^2), \forall 0 \leq \varepsilon < 1\)。这个公式可以通过对于 \(\ln(1 + x)\) 的泰勒级数来说明。（可恶，我并不会证明这个结论，而且我觉得这个结论的 \(\exists C\) 和 \(\forall \varepsilon\) 可能要调换一下顺序才成立……不过这不影响这个式子能够正确地解决现在的问题）

\[\begin{aligned} P_{n, m} &\geq \exp(-\frac 1m - C\frac 1{m^2})\exp(-\frac 2m - C\frac{2^2}{m^2})\cdots\exp(-\frac{n-1}m - C\frac{(n-1)^2}{m^2}) \\ &= \exp\left(-\frac{n(n-1)}{2m}\right)\exp\left( -\frac C{m^2}\left(1^2 + 2^2 + \dots + (n-1)^2 \right) \right)\\ &= \exp\left(-\frac{n(n-1)}{2m}\right)\exp\left(-O\left(\frac{n^3}{m^2}\right)\right)\\ &= \exp\left(-\frac{n(n-1)}{2m}\right)\left(1-O\left(\frac{n^3}{m^2}\right)\right) \end{aligned} \]

这里分子上的 \((n-1)\) 处理起来很不方便，我们希望能将分子化成 \(n^2\) 的形式：

\[\begin{aligned} \exp\left(-\frac{n(n-1)}{2m}\right) &= \exp\left(-\frac{n^2}{2m} + \frac n{2m}\right)\\ &= \exp\left(-\frac{n^2}{2m}\right)\exp\left(\frac n{2m}\right)\\ &= \exp\left(-\frac{n^2}{2m}\right)\left(1 + O\left(\frac n{m}\right)\right) \end{aligned} \]

于是我们得到

\[P_{n, m} = \exp\left(-\frac{n^2}{2m}\right)\left(1 + O\left(\frac n{m}\right)\right)\left(1-O\left(\frac{n^3}{m^2}\right)\right) \]

当 \(n\) 远小于 \(m\) 的时候，后面两项带来的误差都很小。但我们仍然想知道哪一项才是主导的误差项。事实上，当 \(n\) 很小的时候是 \(\left(1 + O\left(\frac n{m}\right)\right)\)，\(n\) 稍大一些时是 \(\left(1-O\left(\frac{n^3}{m^2}\right)\right)\)。其分界点是 \(\frac nm = \frac{n^3}{m^2}\) 即 \(n = \sqrt m\) 时，即

\[P_{n, m} = \exp\left(-\frac{n^2}{2m}\right)\cdot \left\{ \begin{aligned} &1 \pm O\left(\frac n{m}\right)& n \leq \sqrt m\\ &1\pm O\left(\frac{n^3}{m^2}\right) & n \geq \sqrt m \end{aligned} \right. \]

生日问题关心的是什么时候碰撞的概率会超过 \(0.5\)。因此我们只需要令 \(P_{n, m} \approx \exp\left(-\frac{n^2}{2m}\right) = \frac 12\) 即可，则 \(n = \sqrt{2\ln 2}\sqrt m = \Theta（\sqrt m)\)。

此时的 \(n \geq \sqrt m\)，所以我们可以说 \(n = \sqrt{2\ln 2}\sqrt m \pm O(1)\) 时，\(P_{n, m} = \frac 12 \pm O(\frac 1{\sqrt m})\)。