Java实现二叉搜索树

将链表进行改造，即可构造一棵二叉树。

本文用java实现一颗二叉搜索树，实现二叉树的新增，删除，查找等功能。并测试新增和查找的时间复杂度。

节点类与链表节点相似，将链表的前后节点定义逻辑改为左右（孩子）节点：

/**
 * 二叉搜索树节点
 */
public class Node
{
    private int data;//数据域
    private Node left;//左节点（左孩子）
    private Node right;//右节点（右孩子）

    public int getData() {
        return data;
    }
    public void setData(int data) {
        this.data = data;
    }
    public Node getLeft() {
        return left;
    }
    public void setLeft(Node left) {
        this.left = left;
    }
    public Node getRight() {
        return right;
    }
    public void setRight(Node right) {
        this.right = right;
    }

    //构造函数
    public Node(int data, Node left, Node right){
        this.data = data;
        this.left = left;
        this.right = right;
    }
    public Node(int data){
        this(data,null,null);
    }
    public Node(){
        this(0,null,null);
    }

}

二叉搜索树的实现：

/**
 * 二叉搜索树
 * Author:hangwei
 * Date:2022/11
 */
public class SearchTree {
    private Node root;
    public Node getRoot() {
        return root;
    }
    public void setRoot(Node root) {
        this.root = root;
    }

    //查找树中是否存在某个值
    public Node search(Node root,int val){
        int nums = 0;
        while (root != null && root.getData() != val){
            if(val < root.getData())//位于左子树
                root = root.getLeft();//缩小范围
            else
                root = root.getRight();
            nums++;
        }
        System.out.println("本次查找执行了："+nums+"次");
        return root;
    }

    int addCount = 0;
    //给树新增节点
    public void Add(Node root,int val){
        if(val == 30)
            addCount++;
        if(root == null) {
            setRoot(new Node(val));
        }
        else {
            if(val < root.getData()){
                if(root.getLeft() == null)//左子树为空新增
                    root.setLeft(new Node(val));
                else
                    Add(root.getLeft(),val);//缩小子树范围并递归
            }
            else {
                if(root.getRight() == null)//右子树为空新增
                    root.setRight(new Node(val));
                else
                    Add(root.getRight(), val);
            }
            //验证插入的时间复杂度
            if(root.getRight()!=null && root.getRight().getData() == 30)
                System.out.println("本次新增节点30执行了："+addCount+" 次");
        }

    }
    public Node delete(Node root,int val){
        if(root == null)
            return root;
        if(root.getData() == val){//找到节点
            if(root.getLeft() == null && root.getRight() ==null){//1，左右子节点为空则直接返回空
                return null;
            } else if (root.getLeft() == null) {//2，左孩子节点为空则返回右孩子节点
                return root.getRight();
            } else if (root.getRight() == null) {//3，右孩子节点为空则返回左孩子节点
                return root.getLeft();
            }
            else {//4，左右孩子节点都不为空
                Node cur = root.getRight();
                while (cur.getLeft() !=null)//如果右节点有孩子节点且左孩子不为空
                    cur = cur.getLeft();//找到右节点的最小左孩子
                cur.setLeft(root.getLeft());//因为被删除目标节点的右子树始终比左子树大，所以找到右子树的最小左孩子，并设置最小左孩子的左子树为目标节点的左子树
                return root.getRight();
            }
        }
        else if(val < root.getData())//处理左子树
            root.setLeft(delete(root.getLeft(),val));
        else//处理右子树
            root.setRight(delete(root.getRight(),val));
        return root;
    }
}

测试类：

import java.util.*;

public class Main {
    public static void main(String[] args) {
        /**
         * 假设有一颗二叉搜索树，总结点树是n，高度是h，根节点的高度是1，假设也是满二叉树，
         * 则n与h的关系：n=2^h - 1;(极端情况n=h暂不考虑退化到链表的情况)
         * 即：h=log2^(n+1)
         */
        //二叉搜索树测试
        SearchTree st = new SearchTree();
        //插入节点&验证插入的时间复杂度
        st.Add(null,25);
        st.Add(st.getRoot(),18);
        st.Add(st.getRoot(),16);
        st.Add(st.getRoot(),19);
        st.Add(st.getRoot(),29);
        st.Add(st.getRoot(),27);
        st.Add(st.getRoot(),30);

        //输出树
        System.out.println(Arrays.toString(levelOrder(st.getRoot())));
        //查找
        System.out.println(st.search(st.getRoot(),27).getData());
        System.out.println(st.search(st.getRoot(),30).getData());
        System.out.println(st.search(st.getRoot(),31));
        //验证查找的时间复杂度

        //删除节点
        st.delete(st.getRoot(),30);
        //再次输出树
        System.out.println(Arrays.toString(levelOrder(st.getRoot())));
        //删除节点
        st.delete(st.getRoot(),18);
        //再次输出树
        System.out.println(Arrays.toString(levelOrder(st.getRoot())));
    }


    /**
     * 层序遍历
     * @param root
     * @return
     */
    public static int[] levelOrder(Node root) {
        if(root == null){
            return new int[0];
        }

        Queue<Node> queue = new LinkedList<Node>();
        queue.add(root);
        ArrayList<Integer> arr = new ArrayList<>();
        while( !queue.isEmpty() ){
            Node temp = queue.poll();
            arr.add(temp.getData());
            if(temp.getLeft() != null){
                queue.add(temp.getLeft());
            }
            if(temp.getRight() != null){
                queue.add(temp.getRight());
            }
        }
        int[] res = new int[arr.size()];
        for(int i = 0;i < arr.size();i++){
            res[i] = arr.get(i);
        }

        return res;

    }

}

执行结果：

 

 

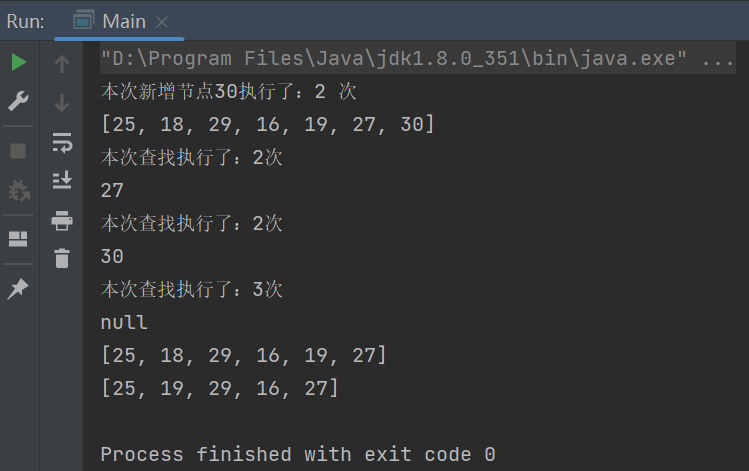
*重点：

1，双向链表即可改造成二叉树；

2，二叉搜索树定义：左子树小于根节点，右子树大于根节点，左子树和右子树的子树一样符合这个定义；

3，新增，查找，删除方法中无处不在的递归思路；

4，层序遍历和时间复杂度验证。