模拟退火学习笔记
模拟退火学习笔记
前言
不知道为啥突然有闲情学这个...
模拟退火 (Simulated Annealing) , 简称 \(SA\) .
是一种基于随机化的算法，无门槛，主要是为了骗分...
不是正解！！！！
根据 爬山算法 的过程，我们发现：对于一个当前最优解附近的非最优解，爬山算法直接舍去了这个解。而很多情况下，我们需要去接受这个非最优解从而跳出这个局部最优解，即为模拟退火算法。
关于退火
什么是退火?
退火是一种金属热处理工艺，指的是将金属缓慢加热到一定温度，保持足够时间，然后以适宜速度冷却。目的是降低硬度，改善切削加工性；消除残余应力，稳定尺寸，减少变形与裂纹倾向；细化晶粒，调整组织，消除组织缺陷。准确的说，退火是一种对材料的热处理工艺，包括金属材料、非金属材料。而且新材料的退火目的也与传统金属退火存在异同。
贺的百度百科
设 \(E| \{x_i\} |\) 表示某一物质体系在微观状态 \(\{x_i\}\) 下的内能，对于给定温度 \(T\) , 若体系处于热平衡态时， \(E |\{x_i\}|\) 服从 Boltzmann 分布：
\[f = c(T) \times e ^ {- \frac{E|\{x_i\}|}{k \times T}} \]其中 \(k\) 为 Boltzmann 常数。
\(T\) 下降， \(E\) 随之下降。只要温度下降足够慢，体系可以长久保持热平衡态。
当我们退火时，刚开始的时候温度高，分子运动剧烈，变化率较高；
然而对于温度降下来之后，分子逐渐趋于稳定，于是分子变化比较小。
模拟退火，就是模拟的这个过程。
具体实现
当然，什么都不能摆脱随机化。
我们设初始温度 \(T_0 > 1000\) , 降温系数 \(\zeta = \{0.996 , 0.995 , \dots\}\) , 末尾温度 \(T_k > 0\) , 在 \(10 ^ {-15}\) 左右 .
对于我们的新横坐标来说，显然他要有局部的特性，并随时间的延长，温度下降，转移地方要更加稳定，就是离旧的横坐标近一点，因此在随机时要有 \(T\) 这个自变量。
然而对于我们新的这个值 \(y\) , 旧的值为 \(x\) , \(\Delta = y - x\)
退火的过程、转移的概率如下：
为什么会存在第二种转移呢？
是为了跳出局部最优解，可能进入新的更优解的地方。
贴图：
具体实现 [JSOI2004] 平衡点 / 吊打XXX
题目描述
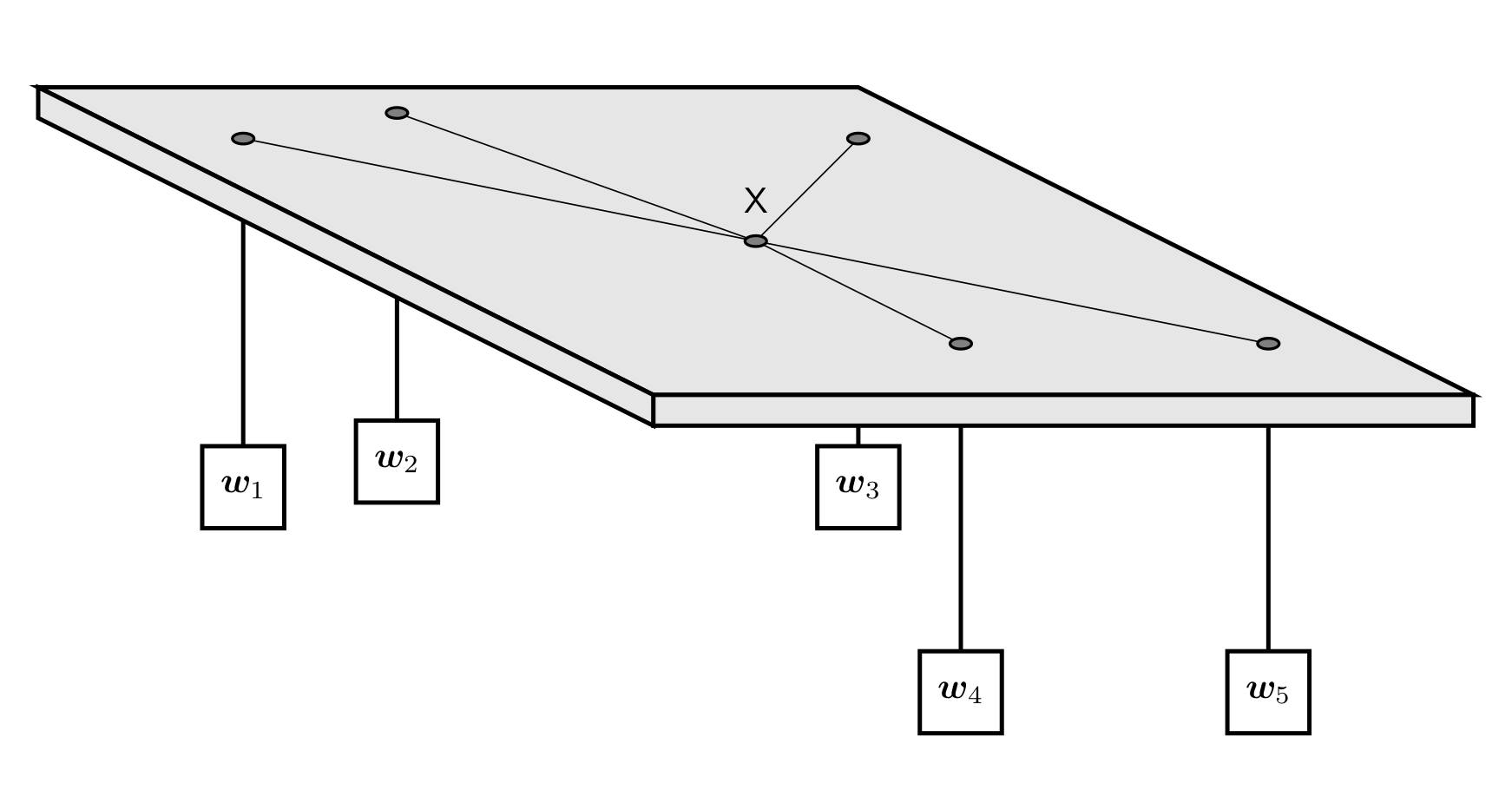
如图，有 \(n\) 个重物，每个重物系在一条足够长的绳子上。
每条绳子自上而下穿过桌面上的洞，然后系在一起。图中 \(x\) 处就是公共的绳结。假设绳子是完全弹性的（即不会造成能量损失），桌子足够高（重物不会垂到地上），且忽略所有的摩擦，求绳结 \(x\) 最终平衡于何处。
注意：桌面上的洞都比绳结 \(x\) 小得多，所以即使某个重物特别重，绳结 \(x\) 也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。
\(1\le n\le 1000\)
\(-10000\le x_i,y_i\le10000, 0<w_i\le1000\)】
题解
假设平衡点坐标为 \((X , Y)\)
那么对于一个重物(坐标为 \(x_i , y_i\) )贡献的重力势能为：
\(E = \sqrt{(X - x_i) ^ 2 + (Y - y_i) ^ 2} \times w_i\)
我们是需要将所有的势能和最小化即可。
注意因为我们为了让答案尽可能的对， \(SA\) 过程要跑很多遍。
CODE
#include <bits/stdc++.h>
using namespace std ;
#define int long long
const int N = 2e5 + 100 ;
inline int read() {
int x = 0 , f = 1 ;
char c = getchar() ;
while (c < '0' || c > '9') {
if (c == '-') f = -f ;
c = getchar() ;
}
while (c >= '0' && c <= '9') {
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
struct Physics {
int x , y , gravity ;
} a[N] ;
int n ; double first , second , ans = 1000000000 , averx , avery ;
void Energy(double x , double y , double & statics) {
statics = 0 ;
for (int i = 1 ; i <= n ; ++ i) {
statics += sqrt((x - a[i].x) * (x - a[i].x) + (y - a[i].y) * (y - a[i].y)) * a[i].gravity ;
}
}
void SA() {
double T = 3000 ;
double x = first , y = second , now , delta_E ;
while (T > 1e-16) {
x = first + (rand() * 2ll - RAND_MAX) * T ;
y = second + (rand() * 2ll - RAND_MAX) * T ;
Energy(x , y , now) ; delta_E = now - ans ;
if (delta_E < 0) {
ans = now , first = x , second = y ;
} else if (exp(- delta_E / T) * RAND_MAX > rand()) {
first = x , second = y ;
}
T *= 0.996 ;
}
}
inline void solve() {
SA() ; SA() ; SA() ; SA() ; SA() ;
SA() ; SA() ; SA() ; SA() ; SA() ;
SA() ; SA() ; SA() ; SA() ; SA() ;
SA() ; SA() ; SA() ; SA() ; SA() ;
SA() ; SA() ; SA() ; SA() ; SA() ;
}
double sumx , sumy ;
signed main() {
srand((unsigned long long)(new char)) ;
n = read() ;
for (int i = 1 ; i <= n ; ++ i) {
a[i] = {read() , read() , read()} ;
sumx += a[i].x ; sumy += a[i].y ;
}
averx = 1.0 * sumx / n ;
avery = 1.0 * sumy / n ;
Energy(averx , avery , ans) ;
first = averx , second = avery ;
solve() ;
printf("%.3lf %.3lf" , first , second) ;
}
