后缀数组--SA--字符串
SA (Suffix Array) -- 后缀数组
简介
这里明白两个定义：
\(SA_i\) : 按字典序排列后大小为 \(i\) 的后缀的后缀头的下标。
\(Rank_i\) : 后缀头的下标为 \(i\) 按字典序排列后的排名。
一个显而易见却很重要的结论:
如何进行后缀排序？
\(O(n^2 \log n)\)
jb 方式，直接处理出所有后缀，直接 sort , 字符串匹配的时间复杂度为 \(O(n)\) , 乘在一起是 \(O(n^2\log n)\) 德
\(O(n \log^2n)\)
需要神奇的倍增做法。
这时候我们贴一个图图：
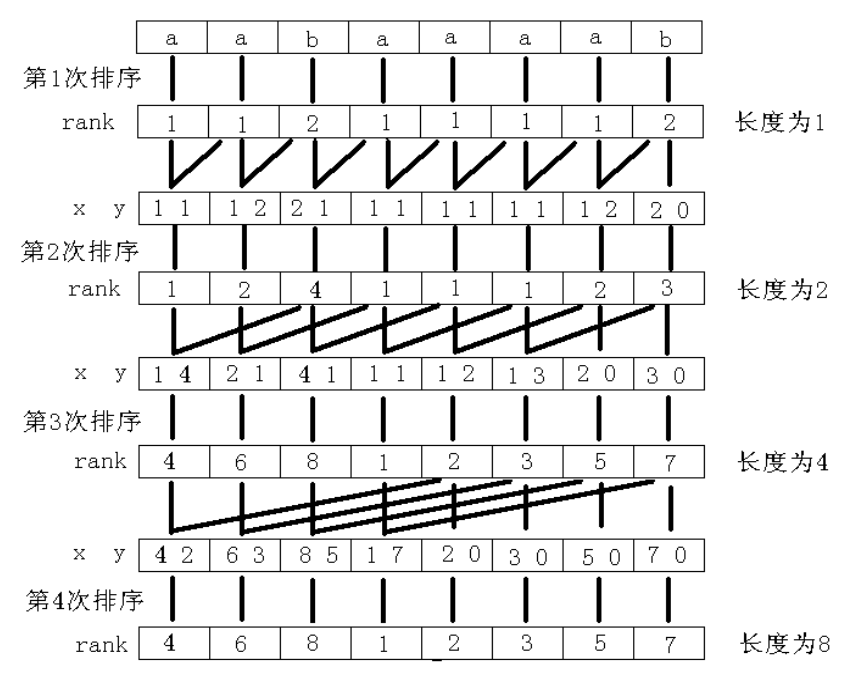
我们先从长度为 \(1\) 开始。 考虑我们更新后的为 \(2\times i\) . 所以只需要将 \(Rank_j\) 和 \(Rank_{\frac{i}{2} + j}\) 作为第一关键字和第二关键字排序即可。
\(O(n\log n)\)
我们发现那个 gb 时间复杂度变为 \(\log^2\) 多乘了一个 \(\log\) 的原因为快速排序。所以考虑 \(O(n)\) 复杂度的排序。
好的通过基数排序就可以进行 \(O(n \log n)\) 了(乐)
但是把这个玩意交到 \(LOJ\) 就发现 \(\color{yellow}T\) .
主要是因为介个玩意常数忒大。
考虑其实我们填一个这个东西本来是第一关键字排好的，其第二关键字在末尾的有可能是 \(0\) , 所以把 \(0\) 的放在最前面，剩下的按原序排好，进行一遍排序即可。
code
CODE
#include <bits/stdc++.h>
#define int long long
using namespace std ;
const int N = 2e6 + 114514 ;
inline int read() {
int x = 0 , f = 1 ;
char c = getchar() ;
while ( c < '0' || c > '9' ) {
f = c == '-' ? -f : f ;
c = getchar() ;
}
while ( c >= '0' && c <= '9' ) {
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
char s[N] ;
int Rank[N] , Lstrk[N] , SA[N] , n , m = 127 ;
int cnt[N] , key1[N] , id[N] , p ;
signed main() {
#ifndef ONLINE_JUDGE
freopen( "1.in" , "r" , stdin ) ;
freopen( "1.out", "w" ,stdout ) ;
#endif
auto compare = [](int x , int y , int j) {
return Lstrk[x] == Lstrk[y] && Lstrk[x + j] == Lstrk[y + j] ;
} ;
cin >> s + 1 ;
n = strlen( s + 1 ) ;
for ( int i = 1 ; i <= n ; ++ i ) { Rank[i] = s[i] ; ++ cnt[Rank[i]] ; }
for ( int i = 1 ; i <= m ; ++ i ) { cnt[i] += cnt[i - 1] ; }
for ( int i = n ; i >= 1 ; -- i ) { SA[cnt[Rank[i]] --] = i ; }
for ( int j = 1 ; ; j <<= 1 , m = p ) {
p = 0 ;
for ( int i = n ; i > n - j ; -- i ) id[++ p] = i ;
for ( int i = 1 ; i <= n ; ++ i ) {
if ( SA[i] - j > 0 ) id[++ p] = SA[i] - j ;
}
memset( cnt , 0 , sizeof(cnt) ) ;
for ( int i = 1 ; i <= n ; ++ i ) { ++ cnt[key1[i] = Rank[id[i]]] ; }
for ( int i = 1 ; i <= m ; ++ i ) { cnt[i] += cnt[i - 1] ; }
for ( int i = n ; i >= 1 ; -- i ) { SA[cnt[key1[i]] --] = id[i] ; }
memcpy( Lstrk , Rank , sizeof(Rank) ) ;
p = 0 ;
for ( int i = 1 ; i <= n ; ++ i ) {
Rank[SA[i]] = compare( SA[i] , SA[i - 1] , j ) ? p : ++ p ;
}
if ( p == n ) break ;
}
for ( int i = 1 ; i <= n ; ++ i ) {
cout << SA[i] << ' ' ;
}
}
\(height\) 数组
你会后缀排序却不会 \(height\) 数组就像你会求 \(Next\) 数组却不会 \(KMP\) 匹配一样。 —— Wang54321
定义一个东西： \(height_i\) 表示 \(Rank\) 为 \(i\) 的和 \(Rank\) 为 \(i - 1\) 的的 \(LCP\)
即 \(LCP(i , i - 1)\)
证明引理
求的话需要证一个引理：
\[height_{Rank[i]} \ge height_{Rank[i - 1]} - 1 \]
如果 \(height_{Rank[i - 1]} \le 1\) 时，这不显然嘛。
else :
我们将具体的东西表示出来：
\(height_{Rank[i]} = LCP(SA[Rank[i]] , SA[Rank[i] - 1]) = LCP(i , SA[Rank[i] - 1])\)
\(height_{Rank[i - 1]} = LCP(SA[Rank[i - 1]] , SA[Rank[i - 1] - 1]) = LCP(i - 1 , SA[Rank[i - 1] - 1])\)
我们已知 \(height_{Rank[i - 1]}\) 是 \(\ge 1\) 的，设那个 \(1\) 为 \(a\) .
所以 \(i - 1\) 可以设为 \(aAC\) , \(SA[Rank[i - 1] - 1]\) 设为 \(aAD\) .
\(aA\) 为其最长公共前缀。
我们这个 \(C\) 是 \(>\) \(D\) 的。
我们知道 \(i\) 为 \(AC\) 。且 \(SA[Rank[i] - 1]\) 和 \(AC\) 中不含有任何后缀。
所以 \(AD \le SA[Rank[i] - 1] < AC\)
所以一定含有公共前缀 \(A\) .
\(\therefore height_{Rank[i]} \ge height_{Rank[i - 1]} - 1\)
证毕.
求 \(height\)
有了上面的引理就可以求了。代码：
CODE
for ( int i = 1 , k = 0 ; i <= n ; ++ i ) {
if ( Rank[i] == 0 ) continue ;
if ( k ) k -- ;
while ( s[i + k] == s[Rank[i - 1] + k] ) k ++ ;
height[Rank[i]] = k ;
}
\(height\) 的用法
如果你只知道这是个什么玩意却不知道怎么用和不知道显然没什么区别。
一个很明显的东西：
\[LCP(l , r) = \min_{l + 1 \le i \le r}\{height_{i}\} \]
感性理解一下：
这两段之间，如果前缀有变更，就直接没了吧，其实变更处的 \(LCP\) 就是其 \(LCP\) .
然后就可以把两个字符串的公共长度问题变为了 \(RMQ\) 问题。即 \(ST\) 表维护区间最小值了。
例题(后缀数组配合单调栈)： AHOI差异
一个无脑题， \(HASH\) 可过的那种： Sandy 的卡片
